N.13 Com­bin­ing an­gu­lar mo­men­tum fac­tors

An­gu­lar mo­menta from dif­fer­ent sources can be com­bined us­ing the Cleb­sch-Gor­dan co­ef­fi­cients of chap­ter 12.7. For ex­am­ple, you can com­bine or­bital and spin an­gu­lar mo­menta of a par­ti­cle that way, or the an­gu­lar mo­menta of dif­fer­ent par­ti­cles.

But some­times you need to mul­ti­ply an­gu­lar mo­men­tum states of the same source to­gether. For ex­am­ple, you may need to fig­ure out a prod­uct of spher­i­cal har­mon­ics, chap­ter 4.2.3, like

$$Y_{l_1}^{m_1}Y_{l_2}^{m_2}$$

where the po­si­tion co­or­di­nates re­fer to the same par­ti­cle. If you mul­ti­ply a few ex­am­ples from ta­ble 4.3 to­gether, you quickly see that the com­bi­na­tions are not given by the Cleb­sch-Gor­dan co­ef­fi­cients of fig­ure 12.6.

One way to un­der­stand the an­gu­lar mo­men­tum prop­er­ties of the above prod­uct qual­i­ta­tively is to con­sider the case that the sec­ond spher­i­cal har­monic takes the co­or­di­nates of an imag­ined sec­ond par­ti­cle. Then you can use the nor­mal pro­ce­dures to fig­ure out the prop­er­ties of the two-par­ti­cle sys­tem. And you can get the cor­re­spond­ing prop­er­ties of the orig­i­nal one-par­ti­cle sys­tem by re­strict­ing the two-par­ti­cle wave func­tion co­or­di­nates to the sub­set in which the par­ti­cle co­or­di­nates are equal.

Note in do­ing so that an­gu­lar mo­men­tum prop­er­ties are di­rectly re­lated to the ef­fect of co­or­di­nate sys­tem ro­ta­tions, {A.19}. Co­or­di­nate sys­tem ro­ta­tions main­tain equal­ity of par­ti­cle co­or­di­nates; they stay within the sub­set. But in­ner prod­ucts for the two-par­ti­cle sys­tem will ob­vi­ously be dif­fer­ent from those for the re­duced one-par­ti­cle sys­tem.

And Cleb­sch-Gor­dan co­ef­fi­cients are in fact in­ner prod­ucts. They are the in­ner prod­uct be­tween the cor­re­spond­ing hor­i­zon­tal and ver­ti­cal states in fig­ures 12.5 and 12.6. The cor­rect co­ef­fi­cients for the prod­uct above are still re­lated to the Cleb­sch-Gor­dan ones, though you may find them in terms of the equiv­a­lent Wigner 3j co­ef­fi­cients.

Wigner no­ticed a num­ber of prob­lems with the Cleb­sch-Gor­dan co­ef­fi­cients:

1.

Cleb­sch and Gor­dan, and not Wigner, get credit for them.

2.

They are far too easy to type.

3.

They have an in­tu­itive in­ter­pre­ta­tion.

So Wigner changed the sign on one of the vari­ables, took out a com­mon fac­tor, and re­for­mat­ted the en­tire thing as a ma­trix. In short

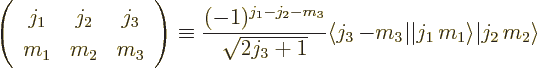$$\left( \begin{array}{ccc} j_1 & j_2 & j_3 \\ m_1 & m_2 ... ...\vert j_1\,m_1\right\rangle}{\left\vert j_2\,m_2\right\rangle}$$ (N.1)

Be­hold, the spank­ing new Wigner 3j sym­bol. Thus Wigner suc­ceeded by his hard work in mak­ing physics a bit more im­pen­e­tra­ble still than be­fore. A big step for physics, a small step back for mankind.

The most im­por­tant thing to note about this sym­bol/co­ef­fi­cient is that it is zero un­less

$$m_1 + m_2 + m_3 = 0 \quad \mbox{and}\quad \vert j_1-j_2\ver... ...eqslant$}}j_3 \mathrel{\raisebox{-.7pt}{$\leqslant$}}j_1 + j_2$$

The right-hand con­di­tions are the so-called tri­an­gle in­equal­i­ties. The or­der­ing of the $j$-​val­ues does not make a dif­fer­ence in these in­equal­i­ties. You can swap the in­dices 1, 2, and 3 ar­bi­trar­ily around.

If all three $m$ val­ues are zero, then the sym­bol is zero if the sum of the $j$ val­ues is odd. If the sum of the $j$ val­ues is even, the sym­bol is not zero un­less the tri­an­gle in­equal­i­ties are vi­o­lated.

If you need an oc­ca­sional value for such a sym­bol that you can­not find in fig­ure 12.5 and 12.6 or more ex­ten­sive ta­bles else­where, there are con­ve­nient cal­cu­la­tors on the web, [[16]]. There is also soft­ware avail­able to eval­u­ate them. Note fur­ther that {D.65} gives an ex­plicit ex­pres­sion.

In lit­er­a­ture, you may also en­counter the so-called Wigner 6j” and “9j sym­bols. They are typ­i­cally writ­ten as

$$\left\{ \begin{array}{ccc} j_1 & j_2 & j_3 \\ l_1 & l_2... ...} & j_{23} \\ j_{31} & j_{32} & j_{33} \end{array} \right\}$$

They ap­pear in the com­bi­na­tion of an­gu­lar mo­menta. If you en­counter one, there are again cal­cu­la­tors on the web. The most use­ful thing to re­mem­ber about 6j sym­bols is that they are zero un­less each of the four tri­ads $j_1j_2j_3$, $j_1l_2l_3$, $l_1j_2l_3$, and $l_1l_2j_3$ sat­is­fies the tri­an­gle in­equal­i­ties.

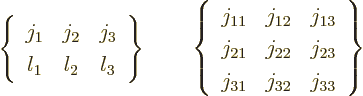
The 9j sym­bol changes by at most a sign un­der swap­ping of rows, or of columns, or trans­pos­ing. It can be ex­pressed in terms of a sum of 6j sym­bols. There are also 12j sym­bols, if you can­not get enough of them.

These sym­bols are needed to do ad­vanced com­pu­ta­tions but these are far out­side the scope of this book. And they are very ab­stract, def­i­nitely not some­thing that the typ­i­cal en­gi­neer would want to get in­volved in in the first place. All that can be done here is to men­tion a few key con­cepts. These might be enough keep you read­ing when you en­counter them in lit­er­a­ture. Or at least give a hint where to look for fur­ther in­for­ma­tion if nec­es­sary.

The ba­sic idea is that it is of­ten nec­es­sary to know how things change un­der ro­ta­tion of the axis sys­tem. Many de­riva­tions in clas­si­cal physics are much sim­pler if you choose your axes clev­erly. How­ever, in quan­tum me­chan­ics you face prob­lems such as the fact that an­gu­lar mo­men­tum vec­tors are not nor­mal vec­tors, but are quan­tized. Then the ap­pro­pri­ate way of han­dling ro­ta­tions is through the so-called Wigner-Eckart the­o­rem. The above sym­bols then pop up in var­i­ous places.

For ex­am­ple, they al­lows you to do such things as fig­ur­ing out the de­riv­a­tives of the har­monic poly­no­mi­als ${\cal{Y}}_l^m$ of ta­ble 4.3, and to de­fine the vec­tor spher­i­cal har­mon­ics $\vec{Y}_{JlM}$ that gen­er­al­ize the or­di­nary spher­i­cal har­mon­ics to vec­tors. A more ad­vanced treat­ment of vec­tor bosons, {A.20}, or pho­ton wave func­tions of def­i­nite an­gu­lar mo­men­tum, {A.21.7}, would use these. And so would a more solid de­riva­tion of the Weis­skopf and Moszkowski cor­rec­tion fac­tors in {A.25.8}. You may also en­counter sym­bols such as ${\cal{D}}_{m'm}^{(j)}$ for ma­trix el­e­ments of fi­nite ro­ta­tions.

All that will be done here is give the de­riv­a­tives of the har­monic poly­no­mi­als $r^lY_l^m$, since that for­mula is not read­ily avail­able. De­fine the fol­low­ing com­plex co­or­di­nates $x_\mu$ for $\mu$ $\vphantom0\raisebox{1.5pt}{$=$}$ $\vphantom{0}\raisebox{1.5pt}{$-$}$1, 0, 1:

$$\mu=-1{:}\quad x_{-1} = \frac{x-{\rm i}y}{\sqrt2} \qquad \... ...= z \qquad \mu=1{:} \quad x_{1} = - \frac{x+{\rm i}y}{\sqrt2}$$

Then

$$\begin{eqnarray*} \frac{\partial r^l Y_l^m}{\partial x_\mu} & = & (-1)^{\mu+1}... ...l-1}Y_{l-1}^{m-\mu} \\ & = & C_{\mu lm} r^{l-1}Y_{l-1}^{m-\mu} \end{eqnarray*}$$

where the in­ner prod­uct of kets is a Cleb­sch-Gor­dan co­ef­fi­cient and

$$\begin{eqnarray*} && \displaystyle C_{-1 lm} = \sqrt{\frac{(2l+1)(l-m)(l-m-1)}... ...isplaystyle C_{1lm} = \sqrt{\frac{(2l+1)(l+m)(l+m-1)}{2(2l-1)}} \end{eqnarray*}$$

or zero if the fi­nal mag­netic quan­tum num­ber is out of bounds.

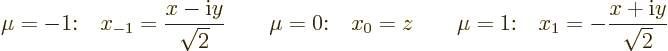
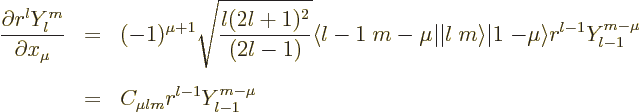
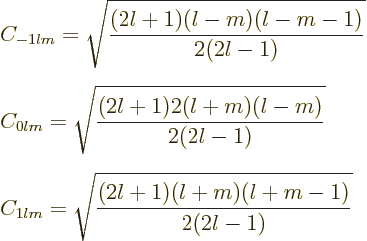
If just hav­ing a rough idea of what the var­i­ous sym­bols are is not enough, you will have to read up on them in a book like [13]. There are a num­ber of such books, but this par­tic­u­lar book has the re­deem­ing fea­ture that it lists some prac­ti­cal re­sults in a us­able form. Some high­lights: gen­eral ex­pres­sion for the Cleb­sch-Gor­dan co­ef­fi­cients on p. 45; wrong de­f­i­n­i­tion of the 3j co­ef­fi­cient on p. 46, (one of the rare mis­takes; cor­rect is above), sym­me­try prop­er­ties of the 3j sym­bol on p. 47; 3j sym­bols with all $m$ val­ues zero on p. 50; list of al­ter­nate no­ta­tions for the Cleb­sch-Gor­dan and 3j co­ef­fi­cients on p.52, (yes, of course it is a long list); in­te­gral of the prod­uct of three spher­i­cal har­mon­ics, like in the elec­tric mul­ti­pole ma­trix el­e­ment, on p. 63; the cor­rect ex­pres­sion for the prod­uct of two spher­i­cal har­mon­ics with the same co­or­di­nates, as dis­cussed above, on p. 63; ef­fect of nu­clear ori­en­ta­tion on elec­tric quadru­pole mo­ment on p. 78; wrong de­riv­a­tives of spher­i­cal har­mon­ics times ra­dial func­tions on p. 69, 80, (an­other 5 rare mis­takes in the sec­ond part of the ex­pres­sion alone, see above for the cor­rect ex­pres­sion for the spe­cial case of har­monic poly­no­mi­als); plane wave in spher­i­cal co­or­di­nates on p. 81. If you do try to read this book, note that $\gamma$ stands for other quan­tum num­bers, as well as the Euler an­gle. That is used well be­fore it is de­fined on p. 33. If you are not psy­chic, it can be dis­tract­ing.