| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
Subsections
A.25 Multipole transitions
This addendum gives a description of the multipole interaction between
atoms or nuclei and electromagnetic fields. In particular, the
spontaneous emission of a photon of electromagnetic radiation in an
atomic or nuclear transition will be examined. But stimulated
emission and absorption are only trivially different.
The basic ideas were already worked out in earlier addenda, especially
in {A.21} on photon wave functions and
{A.24} on spontaneous emission. However, these
addenda left the actual interaction between the atom or nucleus and
the field largely unspecified. Only a very simple form of the
interaction, called the electric dipole approximation, was worked out
there.
Many transitions are not possible by the electric dipole mechanism.
This addendum will describe the more general multipole interaction
mechanisms. That will allow rough estimates of how fast various
possible transitions occur. These will include the Weisskopf and
Moszkowski estimates for the gamma decay of nuclei. It will also allow
a general description exactly how the selection rules of chapter
7.4.4 relate to nuclear and photon wave functions.
The overall picture is that before the transition, the atom or nucleus
is in a high energy state  . Then it transitions
to a lower energy state
. Then it transitions
to a lower energy state  . During the transition
it emits a photon that carries away the excess energy. The energy of
that photon is related to its frequency
. During the transition
it emits a photon that carries away the excess energy. The energy of
that photon is related to its frequency 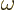 by the
Planck-Einstein relation:
by the
Planck-Einstein relation:
Here 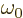 is the nominal frequency of the photon. The actual
photon frequency
is the nominal frequency of the photon. The actual
photon frequency 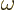 might be slightly different; there can be
some slop in energy conservation. However, that will be taken care of
by using Fermi’s golden rule, chapter 7.6.1.
might be slightly different; there can be
some slop in energy conservation. However, that will be taken care of
by using Fermi’s golden rule, chapter 7.6.1.
It is often useful to express the photon frequency in terms of the
so-called wave number  :
:
Here  is the speed of light. The wave number is a physically
important quantity since it is inversely proportional to the wave
length of the photon. If the typical size of the atom or nucleus is
is the speed of light. The wave number is a physically
important quantity since it is inversely proportional to the wave
length of the photon. If the typical size of the atom or nucleus is
 , then
, then 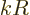 is an nondimensional quantity. It describes the
ratio of atom or nucleus size to photon wave length. Normally this
ratio is very small, which allows helpful simplifications.
is an nondimensional quantity. It describes the
ratio of atom or nucleus size to photon wave length. Normally this
ratio is very small, which allows helpful simplifications.
It will be assumed that only the electrons need to be considered for
atomic transitions. The nucleus is too heavy to move much in such
transitions. For nuclear transitions, (inside the nuclei), it is
usually necessary to consider both types of nucleons, protons and
neutrons. Protons and neutrons will be treated as point particles,
though each is really a combination of three quarks.
As noted in chapter 7.5.3 and 7.6.1, the
driving force
in a transition is the so-called
Hamiltonian matrix element:
Here 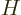 is the Hamiltonian, which will depend on the type of
transition. In particular, it depends on the properties of the
emitted photon.
is the Hamiltonian, which will depend on the type of
transition. In particular, it depends on the properties of the
emitted photon.
If the matrix element 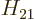 is zero, transitions of that type are
not possible. The transition is
is zero, transitions of that type are
not possible. The transition is forbidden.
If the
matrix element is very small, they will be very slow. (If the term
forbidden
is used without qualification, it indicates
that the electric-dipole type of transition cannot occur,)
A.25.1 Approximate Hamiltonian
The big ideas in multipole transitions are most clearly seen using a
simple model. That model will be explained in this subsection.
However, the results in this subsection will not be quantitatively
correct for multipole transitions of higher order. Later subsections
will correct these deficiencies. This two-step approach is followed
because otherwise it can be easy to get lost in all the mathematics of
multipole transitions. Also, the terminology used in multipole
transitions really arises from the simple model discussed here. And
in any case, the needed corrections will turn out to be very simple.
An electromagnetic wave consists of an electric field  and a
magnetic field
and a
magnetic field 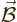 . A basic plane wave takes the form,
(13.10):
. A basic plane wave takes the form,
(13.10):
For convenience the  -axis was taken in the direction of propagation
of the wave. Also the
-axis was taken in the direction of propagation
of the wave. Also the  -axis was taken in the direction of the
electric field. The constant
-axis was taken in the direction of the
electric field. The constant  is the speed of light and the
constant
is the speed of light and the
constant 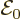 is the root-mean-square value of the electric field.
(The amplitude of the electric field is then
is the root-mean-square value of the electric field.
(The amplitude of the electric field is then 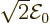 ,
but the root mean square value is more closely related to what you end
up with when the electromagnetic field is properly quantized.)
Finally
,
but the root mean square value is more closely related to what you end
up with when the electromagnetic field is properly quantized.)
Finally 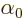 is some unimportant phase angle.
is some unimportant phase angle.
The above waves need to be written as complex exponentials using the
Euler formula (2.5):
Only one of the two exponentials will turn out to be relevant to the
transition process. For absorption that is the first exponential.
But for emission, the case discussed here, the second exponential
applies.
There are different ways to see why only one exponential is relevant.
Chapter 7.7 follows a classical approach in which the field
is given. In that case, the evolution equation that gives the
transition probability is, {D.38},
Here 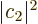 is the transition probability. For emission, the final
state is the low energy state. Then the Planck-Einstein relation
gives the exponential above as
is the transition probability. For emission, the final
state is the low energy state. Then the Planck-Einstein relation
gives the exponential above as 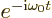 . (By
convention, frequencies are taken to be positive.) Now the
Hamiltonian matrix element
. (By
convention, frequencies are taken to be positive.) Now the
Hamiltonian matrix element 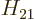 will involve the electric and
magnetic fields, with their exponentials. The first exponentials,
combined with the exponential above, produce a time-dependent factor
will involve the electric and
magnetic fields, with their exponentials. The first exponentials,
combined with the exponential above, produce a time-dependent factor
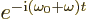 . Since normal photon frequencies
are large, this factor oscillates extremely rapidly in time. Because
of these oscillations, the corresponding terms never produce a
significant contribution to the transition probability. Opposite
contributions average away against each other. So the first
exponentials can be ignored. But the second exponentials produce a
time dependent factor
. Since normal photon frequencies
are large, this factor oscillates extremely rapidly in time. Because
of these oscillations, the corresponding terms never produce a
significant contribution to the transition probability. Opposite
contributions average away against each other. So the first
exponentials can be ignored. But the second exponentials produce a
time dependent factor 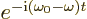 . That does
not oscillate rapidly provided that the emitted photon has frequency
. That does
not oscillate rapidly provided that the emitted photon has frequency
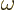
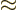
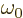 . So such photons can achieve a
significant probability of being emitted.
. So such photons can achieve a
significant probability of being emitted.
For absorption, the low energy state is the first one, instead of the
second. That makes the exponential above 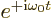 ,
and the entire story inverts.
,
and the entire story inverts.
The better way to see that the first exponentials in the fields drop
out is to quantize the electromagnetic field. This book covers that
only in the addenda. In particular, addendum {A.24}
described the process. Fortunately, quantization of the
electromagnetic field is mainly important to figure out the right
value of the constant 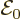 to use, especially for spontaneous
emission. It does not directly affect the actual analysis in this
addendum. In particular the conclusion remains that only the second
exponentials survive.
to use, especially for spontaneous
emission. It does not directly affect the actual analysis in this
addendum. In particular the conclusion remains that only the second
exponentials survive.
The bottom line is that for emission
 |
(A.168) |
Also, as far as this addendum is concerned, the difference between
spontaneous and stimulated emission is only in the value of the
constant 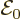 .
.
Next the Hamiltonian is needed. For the matrix element, only the part
of the Hamiltonian that describes the interaction between the atom or
nucleus and the electromagnetic fields is relevant,
{A.24}. (Recall that the matrix element drives the
transition process; no interaction means no transition.) Assume that
the electrons in the atom, or the protons and neutrons in the nucleus,
are numbered using an index  . Then by approximation the
interaction Hamiltonian of a single particle
. Then by approximation the
interaction Hamiltonian of a single particle  with the
electromagnetic field is
with the
electromagnetic field is
In general, you will need to sum this over all particles  .
But the discussion here will usually look at one particle at a time.
.
But the discussion here will usually look at one particle at a time.
The first term in the Hamiltonian above is like the  potential of
gravity, with the particle charge
potential of
gravity, with the particle charge 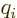 taking the place of the mass
taking the place of the mass
 , the electric field that of the acceleration of gravity
, the electric field that of the acceleration of gravity
 , and the particle position
, and the particle position  that of the height
that of the height
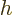 .
.
The second and third terms in the Hamiltonian are due to the fact that
a charged particle that is going around in circles acts as a little
electromagnet. An electromagnet wants to align itself with an ambient
magnetic field. That is just like a compass needle aligns itself with
the magnetic field of earth.
This effect shows up as soon as there is angular momentum. Indeed,
the operator 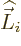 above is the orbital angular momentum of the
particle and
above is the orbital angular momentum of the
particle and 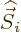 is the spin. The factor
is the spin. The factor  is a
nondimensional number that describes the relative efficiency of the
particle spin in creating an electromagnetic response. For an
electron in an atom,
is a
nondimensional number that describes the relative efficiency of the
particle spin in creating an electromagnetic response. For an
electron in an atom,  is very close to 2. That is a theoretical
value expected for fundamental particles, chapter
13.4. However, for a proton in a nucleus the value
is about 5.6, assuming that the effect of the surrounding protons and
neutrons can be ignored. (Actually, it is quite well established that
normally the surrounding particles cannot be ignored. But it
is difficult to say what value for
is very close to 2. That is a theoretical
value expected for fundamental particles, chapter
13.4. However, for a proton in a nucleus the value
is about 5.6, assuming that the effect of the surrounding protons and
neutrons can be ignored. (Actually, it is quite well established that
normally the surrounding particles cannot be ignored. But it
is difficult to say what value for  to use instead, except that
it will surely be smaller than 5.6, and greater than 2.)
to use instead, except that
it will surely be smaller than 5.6, and greater than 2.)
A special case needs to be made for the neutrons in a nucleus. Since
the neutron has no charge, 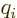
 0, you would expect that its
contribution to the Hamiltonian is zero. However, the final term in
the Hamiltonian is not zero. A neutron has a magnetic
response. (A neutron consists of three charged quarks. The combined
charge of the three is zero, but the combined magnetic response is
not.) To account for that, in the final term, you need to use the
charge
0, you would expect that its
contribution to the Hamiltonian is zero. However, the final term in
the Hamiltonian is not zero. A neutron has a magnetic
response. (A neutron consists of three charged quarks. The combined
charge of the three is zero, but the combined magnetic response is
not.) To account for that, in the final term, you need to use the
charge 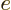 and mass
and mass 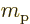 of the proton, and take
of the proton, and take  about
about
 3.8. This value of
3.8. This value of  ignores again the effects of
surrounding protons and neutrons.
ignores again the effects of
surrounding protons and neutrons.
There are additional issues that are important. Often it is assumed
that in a transition only a single particle changes states. If that
particle is a neutron, it might then seem that the first two terms in
the Hamiltonian can be ignored. But actually, the neutron and the
rest of the nucleus move around their common center of gravity. And
the rest of the nucleus is charged. So normally the first two terms
cannot be ignored. This is mainly important for the so-called
electric dipole transitions; for higher multipole orders, the
electromagnetic field is very small near the origin, and the motion of
the rest of the nucleus does not produce much effect. In a transition
of a single proton, you may also want to correct the first term for
the motion of the rest of the nucleus. But also note that the rest of
the nucleus is not really a point particle. That may make a
significant difference for higher multipole orders. Therefore simple
corrections remain problematic. See [33] and
[11] for further discussion of these nontrivial
issues.
The given Hamiltonian ignores the fact that the electric and magnetic
fields are unsteady and not uniform. That is the reason why the
higher multipoles found in the next subsection will not be quite
right. They will be good enough to show the basic ideas however. And
the quantitative problems will be corrected in later subsections.
A.25.2 Approximate multipole matrix elements
The last step is to write down the matrix element. Substituting the
approximate Hamiltonian and fields of the previous subsection into the
matrix element of the introduction gives:
This will normally need to be summed over all electrons  in the
atom, or all nucleons
in the
atom, or all nucleons  in the nucleus. Note that the time
dependent part of the exponential is of no interest. It will in fact
not even appear when the electromagnetic field is properly quantized,
{A.24}. In a classical treatment, it drops out versus
the
in the nucleus. Note that the time
dependent part of the exponential is of no interest. It will in fact
not even appear when the electromagnetic field is properly quantized,
{A.24}. In a classical treatment, it drops out versus
the 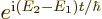 exponential mentioned in the previous
subsection.
exponential mentioned in the previous
subsection.
To split the above matrix element into different multipole orders,
write the exponential as a Taylor series:
In the second equality, the summation index was renotated as 

 . The reason is that
. The reason is that  turns out to be what is
conventionally defined as the multipole order.
turns out to be what is
conventionally defined as the multipole order.
Using this Taylor series, the matrix element gets split into separate
electric and magnetic multipole contributions:
The terms with 
 1 are the dipole ones,
1 are the dipole ones, 
 2 the
quadrupole ones, 3 the octupole ones, 4 the hexadecapole ones,
etcetera. Superscript
2 the
quadrupole ones, 3 the octupole ones, 4 the hexadecapole ones,
etcetera. Superscript  indicates an electric contribution,
indicates an electric contribution,
 a magnetic one. The first contribution that is nonzero
gives the lowest multipole order that is allowed.
a magnetic one. The first contribution that is nonzero
gives the lowest multipole order that is allowed.
A.25.3 Corrected multipole matrix elements
The multipole matrix elements of the previous subsection were rough
approximations. The reason was the approximate Hamiltonian that was
used. This subsection will describe the corrections needed to fix
them up. It will still be assumed that the atomic or nuclear
particles involved are nonrelativistic. They usually are.
The corrected Hamiltonian is
![\begin{displaymath}
\fbox{$\displaystyle
H = \sum_i \left[\frac{1}{2m_i}\left(...
...{\cal B}_i \cdot {\skew 6\widehat{\vec S}}_i \right] + V
$} %
\end{displaymath}](img4799.gif) |
(A.169) |
where the sum is over the individual electrons in the atom or the
protons and neutrons in the nucleus. In the sum, 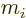 is the mass of
the particle,
is the mass of
the particle, 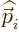 its momentum, and
its momentum, and 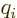 its charge. The
potential
its charge. The
potential  is the usual potential that keeps the particle inside
the atom or nucleus. The remaining parts in the Hamiltonian express
the effect of the additional external electromagnetic field. In
particular,
is the usual potential that keeps the particle inside
the atom or nucleus. The remaining parts in the Hamiltonian express
the effect of the additional external electromagnetic field. In
particular, 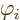 is the electrostatic potential of the field
and
is the electrostatic potential of the field
and 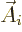 the so-called vector potential, each evaluated at the
particle position. Finally
the so-called vector potential, each evaluated at the
particle position. Finally
is the magnetic part of the field. The spin 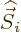 of the particle
interacts with this field at the location of the particle, with a
relative strength given by the nondimensional constant
of the particle
interacts with this field at the location of the particle, with a
relative strength given by the nondimensional constant  .
See chapter 1.3.2 for a classical justification of this
Hamiltonian, or chapter 13 for a quantum one.
.
See chapter 1.3.2 for a classical justification of this
Hamiltonian, or chapter 13 for a quantum one.
Nonrelativistically, the spin does not interact with the electric
field. That is particularly limiting for the neutron, which has no
net charge to interact with the electric field. In reality, a rapidly
moving particle with spin will also interact with the electric field,
{A.39}. See the Dirac equation and in particular
{D.74} for a relativistic description of the
interaction of spin with an electromagnetic field. That would be too
messy to include here, but it can be found in [44]. Note
also that since in reality the neutron consists of three quarks, that
should allow it to interact directly with a nonuniform electric field.
If the field is quantized, you will also want to include the
Hamiltonian of the field in the total Hamiltonian above. And the
field quantities become operators. That goes the same way as in
{A.24}. It makes no real difference for the analysis
in this addendum.
It is always possible, and a very good idea, to take the unperturbed
electromagnetic potentials so that
See for example the addendum on photon wave functions
{A.21} for more on that. That addendum also gives the
potentials that correspond to photons of definite linear, respectively
angular momentum. These will be used in this addendum.
The square in the above Hamiltonian may be multiplied out to give
The term  is the Hamiltonian of the atom or nucleus in the
absence of interaction with the external electromagnetic field. Like
in the previous subsection, it is not directly relevant to the
interaction with the electromagnetic field. Note further that
is the Hamiltonian of the atom or nucleus in the
absence of interaction with the external electromagnetic field. Like
in the previous subsection, it is not directly relevant to the
interaction with the electromagnetic field. Note further that 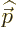 and
and  commute because
commute because 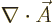 is zero. The term
proportional to
is zero. The term
proportional to 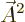 will be ignored as it is normally very small.
(It gives rise to two-photon emission, [33].)
will be ignored as it is normally very small.
(It gives rise to two-photon emission, [33].)
That makes the interaction Hamiltonian of a single particle  equal to
equal to
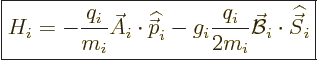 |
(A.170) |
Note that the final spin term has not changed from the approximate
Hamiltonian written down earlier. However, the first term appears
completely different from before. Still, there must obviously be a
connection.
To find that connection requires considerable manipulation. First the
vector potential  must be identified in terms of the simple
electromagnetic wave as written down earlier in (A.168). To
do so, note that the vector potential must be related to the fields as
must be identified in terms of the simple
electromagnetic wave as written down earlier in (A.168). To
do so, note that the vector potential must be related to the fields as
See, for example, {A.21} for a discussion. That allows
the vector potential corresponding to the simple wave (A.168)
to be identified as:
This wave can be generalized to allow general directions of wave
propagation and fields. That gives:
Here the unit vector 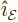 is in the direction of the electric
field and
is in the direction of the electric
field and 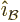 in the direction of the magnetic field. A unit
vector
in the direction of the magnetic field. A unit
vector 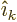 in the direction of wave propagation can be defined
as their cross product. This defines the wave number vector as
in the direction of wave propagation can be defined
as their cross product. This defines the wave number vector as
The three unit vectors are orthonormal. Note that for a given
direction of wave propagation 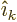 , there will be two
independent waves. They differ in the direction of the electric field
, there will be two
independent waves. They differ in the direction of the electric field
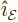 . The choice for the direction of the electric field
for first wave is not unique; the field must merely be orthogonal to
the direction of wave propagation. An arbitrary choice must be made.
The electric field of the second wave needs to be orthogonal to that
of the first wave. The example in the previous subsections took the
wave propagation in the
. The choice for the direction of the electric field
for first wave is not unique; the field must merely be orthogonal to
the direction of wave propagation. An arbitrary choice must be made.
The electric field of the second wave needs to be orthogonal to that
of the first wave. The example in the previous subsections took the
wave propagation in the  -direction,
-direction, 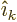

 ,
and the electric field in the
,
and the electric field in the  -direction,
-direction, 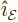

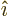 , to give the magnetic field in the
, to give the magnetic field in the  -direction,
-direction,
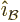

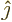 . In that case the second independent
wave will have its electric field in the
. In that case the second independent
wave will have its electric field in the  -direction,
-direction, 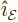

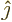 , and its magnetic field in the negative
, and its magnetic field in the negative
 -direction,
-direction, 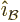


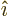 .
.
The single-particle matrix element is now, dropping again the
time-dependent factors,
The first term needs to be cleaned up to make sense out of it. That
is an extremely messy exercise, banned to {D.43}.
However, the result is much like before:
where
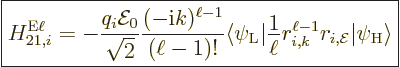 |
(A.171) |
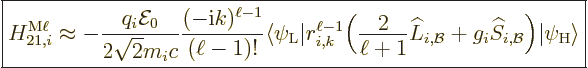 |
(A.172) |
Here 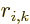 is the component of the position of the particle in the
direction of motion. Similarly,
is the component of the position of the particle in the
direction of motion. Similarly,  is the component of
position in the direction of the electric field, while the angular
momentum components are in the direction of the magnetic field.
is the component of
position in the direction of the electric field, while the angular
momentum components are in the direction of the magnetic field.
This can now be compared to the earlier results using the approximate
Hamiltonian. Those earlier results assumed the special case that the
wave propagation was in the  -direction and had its electric field
in the
-direction and had its electric field
in the  -direction. In that case,
-direction. In that case,
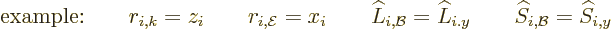 |
(A.173) |
Noting that, it is seen that the correct electric contributions only
differ from the approximate ones by a simple factor 1/ .
This factor is 1 for electric dipole contributions, so these were
correct already. Similarly, the magnetic contribution differs only by
the additional factor 2
.
This factor is 1 for electric dipole contributions, so these were
correct already. Similarly, the magnetic contribution differs only by
the additional factor 2
 for the orbital angular momentum
from the approximate result. This factor is 1 for magnetic dipole
contributions. So these too were already correct.
for the orbital angular momentum
from the approximate result. This factor is 1 for magnetic dipole
contributions. So these too were already correct.
However, there is a problem with the electric contribution in the case
of nuclei. A nuclear potential does not just depend on the position
of the nuclear particles, but also on their momentum. That introduces
an additional term in the electric contribution, {D.43}.
A ballpark for that term shows that this may well make the listed
electric contribution quantitatively invalid, {N.14}.
Unfortunately, nuclear potentials are not known to sufficient accuracy
to give a solid prediction for the contribution. In the following,
this problem will usually simply be ignored, like other textbooks do.
A.25.4 Matrix element ballparks
Recall that electromagnetic transitions are driven by the matrix
element. The previous subsection managed to split the matrix element
into separate electric and magnetic multipole contributions. The
intent in this subsection is now to show that normally, the first
nonzero multipole contribution is the important one. Subsequent
multipole contributions are normally small compared to the first
nonzero one.
To do so, this subsection will ballpark the multipole contributions.
The ballparks will show that the magnitude of the contributions
decreases rapidly with increasing multipole order  .
.
But of course ballparks are only that. If a contribution is exactly
zero for some special reason, (usually a symmetry), then the ballpark
is going to be wrong. That is why it is the first nonzero
multipole contribution that is important, rather than simply the first
one. The next subsection will discuss the so-called selection rules
that determine when contributions are zero.
The ballparks are formulated in terms a typical size  of the atom
or nucleus. For the present purposes, this size will be taken to be
the average radial position of the particles away from the center of
atom or nucleus. Then the magnitudes of the electric multipole
contributions can be written as
of the atom
or nucleus. For the present purposes, this size will be taken to be
the average radial position of the particles away from the center of
atom or nucleus. Then the magnitudes of the electric multipole
contributions can be written as

There is no easy way to say exactly what the inner product above will
be. However, since the positions inside it have been scaled with the
mean radius  , its value is supposedly some normal finite
number. Unless the inner product happens to be zero for some special
reason of course. Assuming that this does not happen, the inner
product can be ignored for the ballpark. And that then shows that
each higher nonzero electric multipole contribution is smaller than
the previous one by a factor
, its value is supposedly some normal finite
number. Unless the inner product happens to be zero for some special
reason of course. Assuming that this does not happen, the inner
product can be ignored for the ballpark. And that then shows that
each higher nonzero electric multipole contribution is smaller than
the previous one by a factor 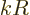 . Now
. Now  is inversely
proportional to the wave length of the photon that is emitted or
absorbed. This wave length is normally very much larger than the size
of the atom or nucleus
is inversely
proportional to the wave length of the photon that is emitted or
absorbed. This wave length is normally very much larger than the size
of the atom or nucleus  . That means that
. That means that 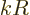 is very small.
And that then implies that a nonzero multipole contribution at a
higher value of
is very small.
And that then implies that a nonzero multipole contribution at a
higher value of  will be very much less than one at a lower
value. So contributions for values of
will be very much less than one at a lower
value. So contributions for values of  higher than the first
nonzero one can normally be ignored.
higher than the first
nonzero one can normally be ignored.
The magnitudes of the magnetic contributions can be written as
Recall that angular momentum values are multiples of  .
Therefore the matrix element can again be ballparked as some finite
number, if nonzero. So once again, the multipole contributions get
smaller by a factor
.
Therefore the matrix element can again be ballparked as some finite
number, if nonzero. So once again, the multipole contributions get
smaller by a factor 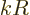 for each increase in order. That means that
the nonzero magnetic contributions too decrease rapidly with
for each increase in order. That means that
the nonzero magnetic contributions too decrease rapidly with
 .
.
That leaves the question how magnetic contributions compare to
electric ones. First compare a magnetic multipole term to the
electric one of the same multipole order  . The above
estimates show that the magnetic term is mainly different from the
electric one by the factor
. The above
estimates show that the magnetic term is mainly different from the
electric one by the factor
Atomic sizes are in the order of an Ångstrom, and nuclear ones in
the order of a few femtometers. So ballpark magnetic contributions
are small compared to electric ones of the same order  .
And more so for atoms than for nuclei. (Transition rates are
proportional to the square of the first nonzero contribution. So the
ballpark transition rate for a magnetic transition is smaller than an
electric one of the same order by the square of the above factor.)
.
And more so for atoms than for nuclei. (Transition rates are
proportional to the square of the first nonzero contribution. So the
ballpark transition rate for a magnetic transition is smaller than an
electric one of the same order by the square of the above factor.)
A somewhat more physical interpretation of the above factor can be
given:
Here  is a ballpark for the kinetic energy
is a ballpark for the kinetic energy

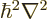

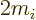 of the particle. Note that this
ballpark is exact for the hydrogen atom ground state if you take the
Bohr radius as the average radius
of the particle. Note that this
ballpark is exact for the hydrogen atom ground state if you take the
Bohr radius as the average radius  of the atom. However, for
heavier atoms and nuclei, this ballpark may be low: it ignores the
exclusion effects of the other particles. Further
of the atom. However, for
heavier atoms and nuclei, this ballpark may be low: it ignores the
exclusion effects of the other particles. Further 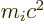 is the
rest mass energy of the particle. Now protons and neutrons in nuclei,
and at least the outer electrons in atoms are nonrelativistic; their
kinetic energy is much less than their rest mass energy. It follows
again that magnetic contributions are normally much smaller than
electric ones of the same multipole order.
is the
rest mass energy of the particle. Now protons and neutrons in nuclei,
and at least the outer electrons in atoms are nonrelativistic; their
kinetic energy is much less than their rest mass energy. It follows
again that magnetic contributions are normally much smaller than
electric ones of the same multipole order.
Compare the magnetic multipole term also to the electric one of the
next multipole order. The trailing factor in the magnetic element can
for this case be written as
The denominator in the final ratio is the energy of the emitted or
absorbed photon. Typically, it is significantly less than the
ballpark kinetic energy of the particle. That then makes magnetic
matrix elements significantly larger than electric ones of the
next-higher multipole order. Though smaller than the electric ones of
the same order.
A.25.5 Selection rules
Based on the ballparks given in the previous subsection, the  electric dipole contribution should dominate transitions. It should
be followed in size by the
electric dipole contribution should dominate transitions. It should
be followed in size by the 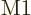 magnetic dipole one, followed by
the
magnetic dipole one, followed by
the 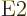 electric quadrupole one, etcetera.
electric quadrupole one, etcetera.
But this order gets modified because matrix elements are very often
zero for special reasons. This was explained physically in chapter
7.4.4 based on the angular momentum properties of the
emitted photon. This subsection will instead relate it directly to
the matrix element contributions as identified in subsection
A.25.3. To simplify the reasoning, it will again be assumed
that the  -axis is chosen in the direction of wave motion and the
-axis is chosen in the direction of wave motion and the
 -axis in the direction of the electric field. So
(A.173) applies for the multipole contributions
(A.171) and (A.172).
-axis in the direction of the electric field. So
(A.173) applies for the multipole contributions
(A.171) and (A.172).
Consider first the electric dipole contribution
 . According to (A.171) and
(A.173) this contribution contains the inner product
. According to (A.171) and
(A.173) this contribution contains the inner product

Why would this be zero? Basically because in the inner product
integrals, positive values of  might exactly integrate away
against corresponding negative values. That can happen because of
symmetries in the nuclear wave functions.
might exactly integrate away
against corresponding negative values. That can happen because of
symmetries in the nuclear wave functions.
One such symmetry is parity. For all practical purposes, atomic and
nuclear states have definite parity. If the positive directions of
the Cartesian axes are inverted, atomic and nuclear states either stay
the same (parity 1 or positive), or change sign (parity  1 or
negative). Assume, for example, that
1 or
negative). Assume, for example, that  and
and
 have both positive parity. That means that they do
not change under an inversion of the axes. But the factor
have both positive parity. That means that they do
not change under an inversion of the axes. But the factor  in
the inner product above has odd parity: axes inversion replaces
in
the inner product above has odd parity: axes inversion replaces  by
by 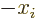 . So the complete inner product above changes sign
under axes inversion. But inner products are defined in a way that
they do not change under axes inversion. (In terms of chapter
2.3, the effect of the axes inversion can be undone by a
further inversion of the integration variables.) Something can only
change sign and still stay the same if it is zero, (
. So the complete inner product above changes sign
under axes inversion. But inner products are defined in a way that
they do not change under axes inversion. (In terms of chapter
2.3, the effect of the axes inversion can be undone by a
further inversion of the integration variables.) Something can only
change sign and still stay the same if it is zero, ( 0 is 0 but say
0 is 0 but say
 5 is not 5).
5 is not 5).
So if both  and
and  have positive parity,
the electric dipole contribution is zero. The only way to get a
nonzero inner product is if exactly one of
have positive parity,
the electric dipole contribution is zero. The only way to get a
nonzero inner product is if exactly one of  and
and
 has negative parity. Then the factor
has negative parity. Then the factor  1 that this
state picks up under axes inversion cancels the
1 that this
state picks up under axes inversion cancels the  1 from
1 from  ,
leaving the inner product unchanged as it should. So the conclusion
is that in electric dipole transitions
,
leaving the inner product unchanged as it should. So the conclusion
is that in electric dipole transitions  and
and
 must have opposite parities. In other words, the
atomic or nuclear parity must
must have opposite parities. In other words, the
atomic or nuclear parity must flip over
in the
transition. This condition is called the parity “selection
rule” for an electric dipole transition. If it is not
satisfied, the electric dipole contribution is zero and a different
contribution will dominate. That contribution will be much smaller
than a typical nonzero electric dipole one, so the transition will be
much slower.
The 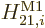 magnetic dipole contribution contains the
inner product
magnetic dipole contribution contains the
inner product
The angular momentum operators do nothing under axes inversion. One
way to see that is to think of  as written in terms of
states of definite
as written in terms of
states of definite  -momentum. Then the angular momentum
operators merely add scalar factors
-momentum. Then the angular momentum
operators merely add scalar factors 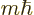 to those states. These
do not affect what happens to the remainder of the inner product under
axes inversion. Alternatively, note that
to those states. These
do not affect what happens to the remainder of the inner product under
axes inversion. Alternatively, note that 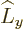

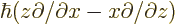

 and each
term has two position coordinates that change sign. And surely spin
should behave the same as orbital angular momentum.
and each
term has two position coordinates that change sign. And surely spin
should behave the same as orbital angular momentum.
If the angular momentum operators do nothing under axes inversion, the
parities of the initial and final atomic or nuclear states will have
to be equal. So the parity selection rule for magnetic dipole
transitions is the opposite from the one for electric dipole
transitions. The parity has to stay the same in the transition.
Assuming again that the wave motion is in the  -direction, each
higher multipole order
-direction, each
higher multipole order  adds a factor
adds a factor  to the electric or
magnetic inner product. This factor changes sign under axes
inversion. So for increasing
to the electric or
magnetic inner product. This factor changes sign under axes
inversion. So for increasing  , alternatingly the atomic
or nuclear parity must flip over or stay the same.
, alternatingly the atomic
or nuclear parity must flip over or stay the same.
If the parity selection rule is violated for a multipole term, the
term is zero. However, if it is not violated, the term may still be
zero for some other reason. The most important other reason is
angular momentum. Atomic and nuclear states have definite angular
momentum. Consider again the electric dipole inner product
States of different angular momentum are orthogonal. That is a
consequence of the fact that the momentum operators are Hermitian.
What it means is that the inner product above is zero unless
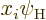 has at least some probability of having the same
angular momentum as state
has at least some probability of having the same
angular momentum as state  . Now the factor
. Now the factor  can be written in terms of spherical harmonics using chapter
4.2.3, table 4.3:
can be written in terms of spherical harmonics using chapter
4.2.3, table 4.3:
So it is a sum of two states, both with square angular momentum
quantum number 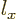
 1, but with
1, but with  angular momentum quantum number
angular momentum quantum number
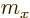

 1, respectively 1.
1, respectively 1.
Now recall the rules from chapter 7.4.2 for combining
angular momenta:
Here 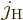 is the quantum number of the square angular momentum
of the atomic or nuclear state
is the quantum number of the square angular momentum
of the atomic or nuclear state  . And
. And
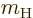 is the quantum number of the
is the quantum number of the  angular momentum of the
state. Similarly
angular momentum of the
state. Similarly  and
and 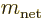 are the possible
values for the quantum numbers of the combined state
are the possible
values for the quantum numbers of the combined state
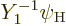 . Note again that
. Note again that 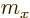 and
and 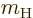 values simply add together. However, the
values simply add together. However, the 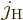 -value
changes by up to
-value
changes by up to 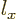
 1 unit in either direction. (But if
1 unit in either direction. (But if
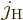
 0, the combined state cannot have zero angular
momentum.)
0, the combined state cannot have zero angular
momentum.)
(It should be noted that you should be careful in combining these
angular momenta. The normal rules for combining angular momenta apply
to different sources of angular momentum. Here the factor  does
not describe an additional source of angular momentum, but a particle
that already has been given an angular momentum within the wave
function
does
not describe an additional source of angular momentum, but a particle
that already has been given an angular momentum within the wave
function  . That means in particular that you
should not try to write out
. That means in particular that you
should not try to write out 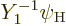 using the
Clebsch-Gordan coefficients of chapter 12.7,
{N.13}. If you do not know what Clebsch-Gordan coefficients
are, you have nothing to worry about.)
using the
Clebsch-Gordan coefficients of chapter 12.7,
{N.13}. If you do not know what Clebsch-Gordan coefficients
are, you have nothing to worry about.)
To get a nonzero inner product, one of the possible states of net
angular momentum above will need to match the quantum numbers
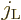 and
and 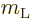 of state
of state  . So
. So
(And if 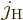
 0,
0, 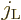 cannot be zero.) But
recall that
cannot be zero.) But
recall that  also contained a
also contained a 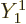 state. That state will
allow
state. That state will
allow 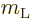

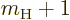 . And if you take a wave
that has its electric field in the
. And if you take a wave
that has its electric field in the  -direction instead of the
-direction instead of the
 -direction, you also get a
-direction, you also get a 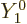 state that gives the possibility
state that gives the possibility
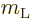

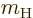 .
.
So the complete selection rules for electric dipole transitions are
where 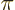 means the parity. In addition, at least one of
means the parity. In addition, at least one of
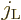 or
or 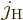 must be nonzero. And as always for these
quantum numbers,
must be nonzero. And as always for these
quantum numbers, 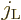
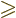 0 and
0 and 

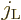 . Equivalent selection rules were written down for
the hydrogen atom with spin-orbit interaction in chapter
7.4.4.
. Equivalent selection rules were written down for
the hydrogen atom with spin-orbit interaction in chapter
7.4.4.
For magnetic dipole transitions, the relevant inner product is
Note that it is either 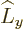 or
or 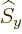 that is applied on
that is applied on
 , not both at the same time. It will be assumed
that
, not both at the same time. It will be assumed
that  is written in terms of states with definite
angular momentum in the
is written in terms of states with definite
angular momentum in the  -direction. In those terms, the effect of
-direction. In those terms, the effect of
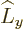 or
or 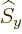 is known to raise or lower the corresponding
magnetic quantum number
is known to raise or lower the corresponding
magnetic quantum number  by one unit, chapter 12.11. Which
means that the net angular momentum can change by one unit. (Like
when opposite orbital angular momentum and spin change into parallel
ones. Note also that for the hydrogen atom in the nonrelativistic
approximation of chapter 4.3, there is no interaction
between the electron spin and the orbital motion. In that case, the
magnetic dipole term can only change the value of
by one unit, chapter 12.11. Which
means that the net angular momentum can change by one unit. (Like
when opposite orbital angular momentum and spin change into parallel
ones. Note also that for the hydrogen atom in the nonrelativistic
approximation of chapter 4.3, there is no interaction
between the electron spin and the orbital motion. In that case, the
magnetic dipole term can only change the value of  or
or  by
one unit. Simply put, only the direction of the angular momentum
changes. That is normally a trivial change as empty space has no
preferred direction.)
by
one unit. Simply put, only the direction of the angular momentum
changes. That is normally a trivial change as empty space has no
preferred direction.)
One big limitation is that in either an electric or a magnetic dipole
transition, the net atomic or nuclear angular momentum  can change
by no more than one unit. Larger changes in angular momentum require
higher multipole orders
can change
by no more than one unit. Larger changes in angular momentum require
higher multipole orders  . These add a factor
. These add a factor
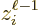 to the inner products. Now it turns out that:
to the inner products. Now it turns out that:
 |
(A.174) |
Here the dots stand for spherical harmonics with lower square angular
momentum. (To verify the above relation, use the Rayleigh formula of
{A.6}, and expand the Bessel function and the
exponential in it in Taylor series.) So the factor 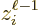 has
a maximum azimuthal quantum number
has
a maximum azimuthal quantum number  equal to
equal to  . That
means that the maximum achievable change in atomic or nuclear angular
momentum increases by one unit for each unit increase in multipole
order
. That
means that the maximum achievable change in atomic or nuclear angular
momentum increases by one unit for each unit increase in multipole
order  .
.
It follows that the first multipole term that can be nonzero has


 , or
, or 
 1 if the
angular momenta are equal. At that multipole level, either the
electric or the magnetic term can be nonzero, depending on parity.
Normally this term will then dominate the transition process, as the
terms of still higher multipole levels are ballparked to be much
smaller.
1 if the
angular momenta are equal. At that multipole level, either the
electric or the magnetic term can be nonzero, depending on parity.
Normally this term will then dominate the transition process, as the
terms of still higher multipole levels are ballparked to be much
smaller.
A further limitation applies to orbital angular momentum. The angular
momentum operators will not change the orbital angular momentum
values. And the factors 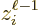 and
and  can only change it
by up to
can only change it
by up to  , respectively 1 units. So the minimum
difference in possible orbital angular momentum values will have to be
no larger than that:
, respectively 1 units. So the minimum
difference in possible orbital angular momentum values will have to be
no larger than that:
 |
(A.175) |
This is mainly important for single-particle states of definite
orbital angular momentum. That includes the hydrogen atom, even with
the relativistic spin-orbit interaction. (But it does assume the
nonrelativistic Hamiltonian in the actual transition process.)
The final limitation is that 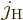 and
and 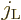 cannot both
be zero. The reason is that if
cannot both
be zero. The reason is that if 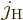 is zero, the possible
angular momentum values of
is zero, the possible
angular momentum values of 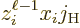 are those of
are those of
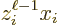 . And those values do not include zero to
match
. And those values do not include zero to
match 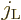
 0. (According to the rules of quantum
mechanics, the probability of zero angular momentum is given by the
inner product with the spherical harmonic
0. (According to the rules of quantum
mechanics, the probability of zero angular momentum is given by the
inner product with the spherical harmonic  of zero angular
momentum. Since
of zero angular
momentum. Since  is just a constant, the inner product is
proportional to the average of
is just a constant, the inner product is
proportional to the average of 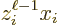 on a spherical
surface around the origin. That average will be zero because by
symmetry positive values of
on a spherical
surface around the origin. That average will be zero because by
symmetry positive values of  will average away against
corresponding negative ones.)
will average away against
corresponding negative ones.)
A.25.6 Ballpark decay rates
It may be interesting to find some actual ballpark values for the
spontaneous decay rates. More sophisticated values, called the
Weisskopf and Moszkowski estimates, will be derived in a later
subsection. However, they are ballparks one way or the other.
It will be assumed that only a single particle, electron or proton,
changes states. It will also be assumed that the first multipole
contribution allowed by angular momentum and parity is indeed nonzero
and dominant. In fact, it will be assumed that this contribution is
as big as it can reasonably be.
To get the spontaneous emission rate, first the proper amplitude
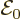 of the electric field to use needs to be identified. The same
relativistic procedure as in {A.24} may be followed to
show it should be taken as
of the electric field to use needs to be identified. The same
relativistic procedure as in {A.24} may be followed to
show it should be taken as
That assumes that the entire system is contained in a very large
periodic box of volume 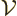 . Also,
. Also, 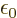
 8.85
10
8.85
10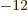 C
C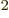 /J m is the permittivity of space
/J m is the permittivity of space
Next, Fermi’s golden rule of chapter 7.6.1 says that
the transition rate is
Here 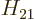 is approximated as the first allowed (nonzero) multipole
contribution
is approximated as the first allowed (nonzero) multipole
contribution 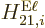 or
or  .
So the additional higher order nonzero contributions are ignored, The
overline means that this contribution needs to be suitably averaged
over all directions of the electromagnetic wave. Further
.
So the additional higher order nonzero contributions are ignored, The
overline means that this contribution needs to be suitably averaged
over all directions of the electromagnetic wave. Further
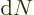

 is the number of photon states in the periodic box
per unit energy range. This is the density of states as given in
chapter 6.3 (6.7). Using the Planck-Einstein
relation it is:
is the number of photon states in the periodic box
per unit energy range. This is the density of states as given in
chapter 6.3 (6.7). Using the Planck-Einstein
relation it is:
Ballpark matrix coefficients were given in subsection A.25.4.
However, a more accurate estimate is desirable. The main problem is
the factor 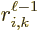 in the matrix elements
(A.171) and (A.172). This factor equals
in the matrix elements
(A.171) and (A.172). This factor equals
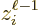 if the
if the  -axis is taken to be in the direction of wave
motion. According to the previous subsection
-axis is taken to be in the direction of wave
motion. According to the previous subsection
The dots indicate spherical harmonics of lower angular momentum that
do not do anything. Only the shown term is relevant for the
contribution of lowest multipole order. So only the shown term should
be ballparked. That can be done by estimating 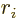 as
as  , and
, and
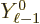 as 1/
as 1/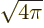 , (which is exact for
, (which is exact for 
 1).
1).
The electric inner product contains a further factor  ,
taking the
,
taking the  -axis in the direction of the electric field. That will
be accounted for by upping the value of
-axis in the direction of the electric field. That will
be accounted for by upping the value of  one unit in the
expression above. The magnetic inner product contains angular
momentum operators. Since not much can be said about these easily,
they will simply be estimated as
one unit in the
expression above. The magnetic inner product contains angular
momentum operators. Since not much can be said about these easily,
they will simply be estimated as  .
.
Putting it all together, the estimated decay rates become
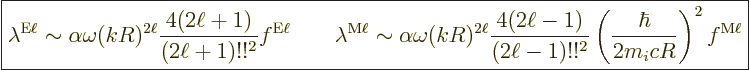 |
(A.176) |
Here
is the so-called fine structure constant. with 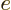
 1.6
10
1.6
10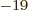 C the proton or electron charge,
C the proton or electron charge, 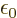
 8.85 10
8.85 10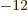 C
C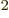 /J m the permittivity of space, and
/J m the permittivity of space, and 
 3 10
3 10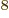 m/s the speed of light. This nondimensional constant gives the strength of
the coupling between charged particles and photons, so it should
obviously be there. The factor
m/s the speed of light. This nondimensional constant gives the strength of
the coupling between charged particles and photons, so it should
obviously be there. The factor 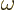 is expected for dimensional
reasons; it gives the decay rate units of inverse time. The nondimensional
factor
is expected for dimensional
reasons; it gives the decay rate units of inverse time. The nondimensional
factor 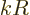 reflects the fact that the atom or nucleus has difficulty
interacting with the photon because its size is so small compared to
the photon wave length. That is worse for higher multipole orders
reflects the fact that the atom or nucleus has difficulty
interacting with the photon because its size is so small compared to
the photon wave length. That is worse for higher multipole orders
 , as their photons produce less of a field near the origin. The
factors
, as their photons produce less of a field near the origin. The
factors 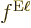 and
and 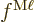 represent unknown
corrections for the errors in the ballparks. These factors are hoped
to be 1. (Fat chance.) As far as the remaining numerical factors are
concerned, ...
represent unknown
corrections for the errors in the ballparks. These factors are hoped
to be 1. (Fat chance.) As far as the remaining numerical factors are
concerned, ...
The final parenthetical factor in the magnetic decay rate was already
discussed in subsection A.25.4. It normally makes magnetic
decays slower than electric ones of the same multipole order, but
faster than electric ones of the next order.
These estimates are roughly similar to the Weisskopf ones. While they
tend to be larger, that is largely compensated for by the fact that in
the above estimates  is the mean radius. In the Weisskopf
estimates it is the edge of the nucleus.
is the mean radius. In the Weisskopf
estimates it is the edge of the nucleus.
In any case, actual decay rates can vary wildly from either pair of
estimates. For example, nuclei satisfy an approximate conservation
law for a quantity called isospin. If the transition violates an
approximate conservation law like that, the transition rate will be
unusually small. Also, it may happen that the initial and final wave
functions have little overlap. That means that the regions where they
both have significant magnitude are small. (These regions should
really be visualized in the high-dimensional space of all the particle
coordinates.) In that case, the transition rate can again be
unexpectedly small.
Conversely, if a lot of particles change state in a transition, their
individual contributions to the matrix element can add up to an
unexpectedly large transition rate.
A.25.7 Wave functions of definite angular momentum
The analysis so far has represented the electromagnetic field in terms
of photon states of definite linear momentum. But it is usually much
more convenient to use states of definite angular momentum. That
allows full use of the conservation laws of angular momentum and
parity.
The states of definite angular momentum have vector potentials given
by the photon wave functions of addendum {A.21.7}.
For electric  and magnetic
and magnetic 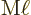 multipole
transitions respectively:
multipole
transitions respectively:
Here 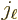 is a spherical Bessel function, {A.6}
and
is a spherical Bessel function, {A.6}
and 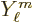 a spherical harmonic, chapter 4.2.3. The
azimuthal angular momentum quantum number of the photon is
a spherical harmonic, chapter 4.2.3. The
azimuthal angular momentum quantum number of the photon is
 . Its quantum number of angular momentum in the chosen
. Its quantum number of angular momentum in the chosen
 -direction is
-direction is  . The electric state has parity
. The electric state has parity
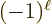 and the magnetic one
and the magnetic one 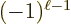 . (That
includes the intrinsic parity, unlike in some other sources). Further
. (That
includes the intrinsic parity, unlike in some other sources). Further
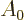 is a constant.
is a constant.
The contribution of a particle  to the matrix element is as before
to the matrix element is as before
But now, for electric transitions 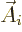 needs to be taken as the
complex conjugate of the photon wave function
needs to be taken as the
complex conjugate of the photon wave function 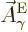 above, evaluated at the position of particle
above, evaluated at the position of particle  . For magnetic
transitions
. For magnetic
transitions 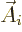 needs to be taken as the complex conjugate of
needs to be taken as the complex conjugate of
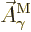 . The complex conjugates are a result of
the quantization of radiation, {A.24}. And they would
not be there for absorption. (The classical reasons are much like the
story for plane electromagnetic waves given earlier. But here the
nonquantized waves are too messy to even bother about, in this
author’s opinion.)
. The complex conjugates are a result of
the quantization of radiation, {A.24}. And they would
not be there for absorption. (The classical reasons are much like the
story for plane electromagnetic waves given earlier. But here the
nonquantized waves are too messy to even bother about, in this
author’s opinion.)
The matrix elements can be approximated assuming that the wave length
of the photon is large compared to the size  of the atom or
nucleus. The approximate contribution of the particle to the
of the atom or
nucleus. The approximate contribution of the particle to the
 electric matrix element is then, {D.43.2},
electric matrix element is then, {D.43.2},
The subscript  on the spherical harmonic means that its arguments
are the coordinates of particle
on the spherical harmonic means that its arguments
are the coordinates of particle  . For nuclei, the above
result is again suspect for the reasons discussed in
{N.14}.
. For nuclei, the above
result is again suspect for the reasons discussed in
{N.14}.
The approximate contribution of the particle to the 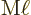 magnetic matrix element is {D.43.2},
magnetic matrix element is {D.43.2},
In general these matrix elements will need to be summed over all
particles.
The above matrix elements can be analyzed similar to the earlier
linear momentum ones. However, the above matrix elements allow you to
keep the atom or nucleus in a fixed orientation. For the linear
momentum ones, the nuclear orientation must be changed if the
direction of the wave is to be held fixed. And in any cases, linear
momentum matrix elements must be averaged over all directions of wave
propagation. That makes the above matrix elements much more
convenient in most cases.
Finally the matrix elements can be converted into spontaneous decay
rates using Fermi’s golden rule of chapter 7.6.1. In
doing so, the needed value of the constant 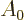 and corresponding
density of states are, following {A.21.7} and
{A.24},
and corresponding
density of states are, following {A.21.7} and
{A.24},
This assumes that the entire system is contained inside a very big
sphere of radius  . This radius
. This radius  disappear in the final answer, and the final decay rates will be the
ones in infinite space. (Despite the absence of
disappear in the final answer, and the final decay rates will be the
ones in infinite space. (Despite the absence of  they
do not apply to a finite sphere, because the density of states above
is an approximation for large
they
do not apply to a finite sphere, because the density of states above
is an approximation for large  .)
.)
It is again convenient to nondimensionalize the matrix elements using
some suitably defined typical atomic or nuclear radius  .
Recent authorative sources, like [33] and
[[4]], take the nuclear radius equal to
.
Recent authorative sources, like [33] and
[[4]], take the nuclear radius equal to
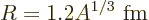 |
(A.177) |
Here  is the number of protons and neutrons in the nucleus and a fm
is 10
is the number of protons and neutrons in the nucleus and a fm
is 10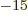 m.
m.
The final decay rates are much like the ones (A.176) found
earlier for linear momentum modes. In fact, linear momentum modes
should give the same answer as the angular ones, if correctly averaged
over all directions of the linear momentum. The decay rates in terms
of angular momentum modes are:
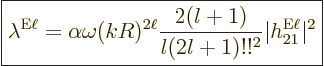 |
(A.178) |
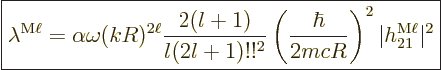 |
(A.179) |
where 
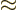 1/137 is again the fine structure constant. The
nondimensional matrix elements in these expressions are
1/137 is again the fine structure constant. The
nondimensional matrix elements in these expressions are
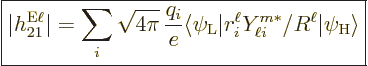 |
(A.180) |
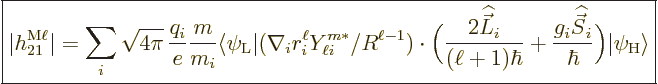 |
(A.181) |
The sum is over the electrons or protons and neutrons, with 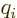 their charge and
their charge and 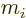 their mass. The reference mass
their mass. The reference mass  would
normally be taken to be the mass of an electron for atoms and of a
proton for nuclei. That means that for the electron or proton the
charge and mass ratios can be set equal to 1. For an electron
would
normally be taken to be the mass of an electron for atoms and of a
proton for nuclei. That means that for the electron or proton the
charge and mass ratios can be set equal to 1. For an electron  is about 2, while for a proton,
is about 2, while for a proton,  would be about 5.6 if the effect
of the neighboring protons and neutrons is ignored. For the neutron,
the (net) charge
would be about 5.6 if the effect
of the neighboring protons and neutrons is ignored. For the neutron,
the (net) charge 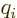 is zero. Therefore the electric matrix element
is zero, and so is the first term in the magnetic one. In the second
term, however, the charge and mass of the proton need to be used,
along with
is zero. Therefore the electric matrix element
is zero, and so is the first term in the magnetic one. In the second
term, however, the charge and mass of the proton need to be used,
along with 

 3.8, assuming again that the effect of
the neighboring protons and neutrons is ignored.
3.8, assuming again that the effect of
the neighboring protons and neutrons is ignored.
A.25.8 Weisskopf and Moszkowski estimates
The Weisskopf and Moszkowski estimates are ballpark spontaneous decay
rates. They are found by ballparking the nondimensional matrix
elements (A.180) and (A.181) given in the
previous subsection. The estimates are primarily intended for nuclei.
However, they can easily be adopted to the hydrogen atom with a few
straightforward changes.
It is assumed that a single proton numbered  makes the transition.
The rest of the nucleus stays unchanged and can therefore be ignored
in the analysis. Note that this does not take into account that the
proton and the rest of the nucleus should move around their common
center of gravity. Correction factors for that can be applied, see
[33] and [11] for more. In a
similar way, the case that a single neutron makes the transition can
be accounted for.
makes the transition.
The rest of the nucleus stays unchanged and can therefore be ignored
in the analysis. Note that this does not take into account that the
proton and the rest of the nucleus should move around their common
center of gravity. Correction factors for that can be applied, see
[33] and [11] for more. In a
similar way, the case that a single neutron makes the transition can
be accounted for.
It is further assumed that the initial and final wave functions of the
proton are of a relatively simple form, In spherical coordinates:
These wave functions are very much like the
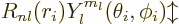 wave functions for the
electron in the hydrogen atom, chapter 4.3. However, for
nuclei, it turns out that you want to combine the orbital and spin
states into states with definite net angular momentum
wave functions for the
electron in the hydrogen atom, chapter 4.3. However, for
nuclei, it turns out that you want to combine the orbital and spin
states into states with definite net angular momentum  and
definite net angular momentum
and
definite net angular momentum 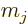 in the chosen
in the chosen
 -direction. Such combinations take the form
-direction. Such combinations take the form
The coefficients 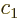 and
and  are of no interest here, but you can
find them in chapter 12.8 2 if needed.
are of no interest here, but you can
find them in chapter 12.8 2 if needed.
In fact even for the hydrogen atom you really want to take the initial
and final states of the electron of the above form. That is due to a
small relativistic effect called “spin-orbit
interaction,” {A.39}. It just so happens that for
nuclei, the spin-orbit effect is much larger. Note however that the
electric matrix element ignores the spin-orbit effect. That is a
significant problem, {N.14}. It will make the
ballparked electric decay rate for nuclei suspect. But there is no
obvious way to fix it.
The nondimensional electric matrix element (A.180) can be
written as an integral over the spherical coordinates of the proton.
It then falls apart into a radial integral and an angular one:
Note that in the angular integral the product of the angular wave
functions implicitly involves inner products between the spin states.
Spin states are orthonormal, so their product is 0 if the spins are
different and 1 if they are the same.
The bottom line is that the square electric matrix element can be
written as a product of a radial factor,
![\begin{displaymath}
f^{\rm rad,\ell}_{\rm LH} \equiv \left[\int R_{\rm {L}}^*(r_i)
(r_i/R)^\ell R_{\rm {H}}(r_i) r_i^2 {\,\rm d}r_i\right]^2 %
\end{displaymath}](img4893.gif) |
(A.182) |
and an angular one,
![\begin{displaymath}
f^{\rm ang,\ell}_{\rm LH} \equiv \left[
\sqrt{4\pi}\! \int...
...m {H}}}
\sin^2\theta_i{\rm d}\theta_i{\rm d}\phi_i\right]^2 %
\end{displaymath}](img4894.gif) |
(A.183) |
As a result, the electric multipole decay rate (A.180)
becomes
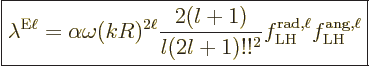 |
(A.184) |
Here the trailing factors represent the square matrix element.
A similar expression can be written for the nondimensional magnetic
matrix element, {D.43.3}: It gives the decay rate
(A.181) as
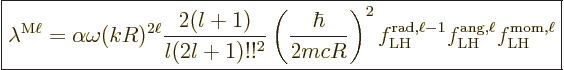 |
(A.185) |
In this case, there is an third factor related to the spin and orbital
angular momentum operators that appear in the magnetic matrix element.
Also, the integrand in the radial factor is one order of  lower
than in the electric element. That is due to the nabla operator
lower
than in the electric element. That is due to the nabla operator
 in the magnetic element. It means that in terms of the
radial electric factor as defined above, the value of
in the magnetic element. It means that in terms of the
radial electric factor as defined above, the value of  to use is
one unit below the actual multipole order.
to use is
one unit below the actual multipole order.
Consider now the values of these factors. The radial factor
(A.182) is the simplest one. The Weisskopf and Moszkowski
estimates use a very crude approximation for this factor. They assume
that the radial wave functions are equal to some constant up to the
nuclear radius  and zero beyond it. (This assumption is not
completely illogical for nuclei, as nuclear densities are fairly
constant until the nuclear edge.) That gives, {D.43.3},
and zero beyond it. (This assumption is not
completely illogical for nuclei, as nuclear densities are fairly
constant until the nuclear edge.) That gives, {D.43.3},
Note that the magnetic decay rate uses  in the denominator
instead of
in the denominator
instead of  because of the lower power of
because of the lower power of  .
.
Table A.1:
Radial integral correction factors for hydrogen atom wave
functions.
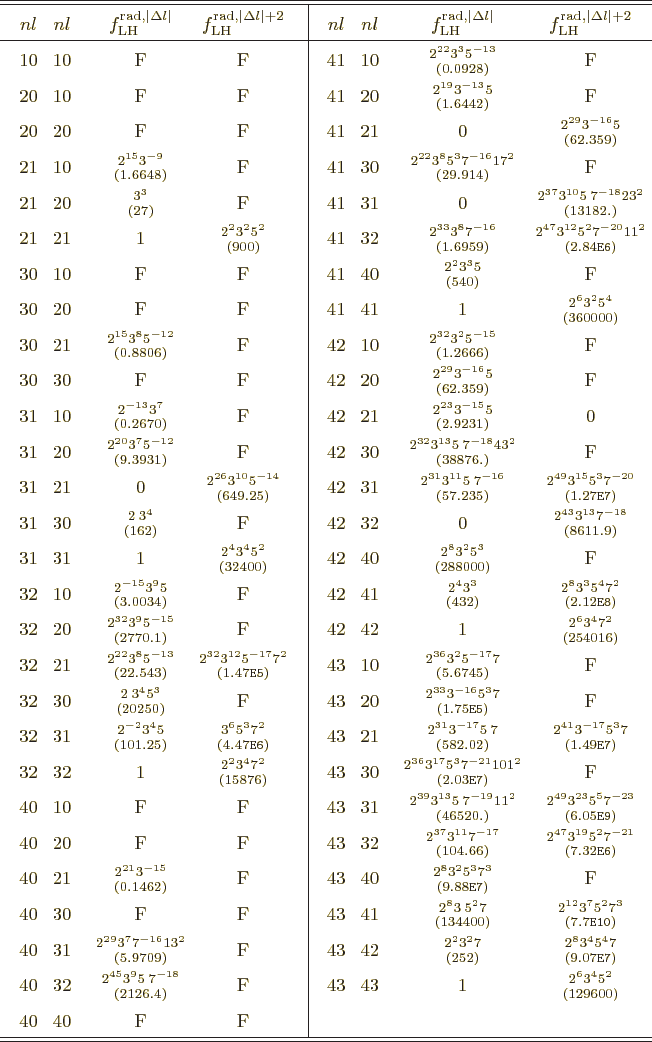 |
More reasonable assumptions for the radial wave functions are
possible. For a hydrogen atom instead of a nucleus, the obvious thing
to do is to use the actual radial wave functions 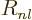 from chapter
4.3. That gives the radial factors listed in table
A.1. These take
from chapter
4.3. That gives the radial factors listed in table
A.1. These take  equal to the Bohr radius. That
explains why some values are so large: the average radial position of
the electron can be much larger than the Bohr radius in various
excited states. In the table,
equal to the Bohr radius. That
explains why some values are so large: the average radial position of
the electron can be much larger than the Bohr radius in various
excited states. In the table,  is the principal quantum number
that gives the energy of the state. Further
is the principal quantum number
that gives the energy of the state. Further  is the azimuthal
quantum number of orbital angular momentum. The two pairs of
is the azimuthal
quantum number of orbital angular momentum. The two pairs of 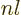 values correspond to those of the initial and final states; in what
order does not make a difference. There are two radial factors listed
for each pair of states. The first value applies to electric and
multipole transitions at the lowest possible multipole order. That is
usually the important one, because normally transition rates decrease
rapidly with multipole order.
values correspond to those of the initial and final states; in what
order does not make a difference. There are two radial factors listed
for each pair of states. The first value applies to electric and
multipole transitions at the lowest possible multipole order. That is
usually the important one, because normally transition rates decrease
rapidly with multipole order.
To understand the given values more clearly, first consider the
relation between multipole order and orbital angular momentum. The
derived matrix elements implicitly assume that the potential of the
proton or electron only depends on its position, not its spin. So
spin does not really affect the orbital motion. That means that the
multipole order for nontrivial transitions is constrained by orbital
angular momentum conservation, [33]:
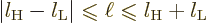 |
(A.186) |
Note that this is a consequence of (A.175) within the
single-particle model. It is just like for the nonrelativistic
hydrogen atom, (7.17). ( transitions that
merely change the direction of the spin, like a
transitions that
merely change the direction of the spin, like a  to
to
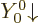 one, are irrelevant since they do not change the energy.
Fermi’s golden rule makes the transition rate for transitions with
no energy change theoretically zero, chapter 7.6.1.)
one, are irrelevant since they do not change the energy.
Fermi’s golden rule makes the transition rate for transitions with
no energy change theoretically zero, chapter 7.6.1.)
The minimum multipole order implied by the left-hand constraint above
corresponds to an electric transition because of parity. However,
this transition may be impossible because of net angular
momentum conservation or because  must be at least 1. That will
make the transition of lowest multipole order a magnetic one. The
magnetic transition still uses the same value for the radial factor
though. The second radial factor in the table is provided since the
next-higher electric multipole order might reasonably compete with the
magnetic one.
must be at least 1. That will
make the transition of lowest multipole order a magnetic one. The
magnetic transition still uses the same value for the radial factor
though. The second radial factor in the table is provided since the
next-higher electric multipole order might reasonably compete with the
magnetic one.
More realistic radial factors for nuclei can be formulated along
similar lines. The simplest physically reasonable assumption is that
the protons and neutrons are contained within an impenetrable sphere
of radius  . A hydrogen-like numbering system of the quantum
states can again be used, figure 14.14, with one
difference. For hydrogen, a given energy level
. A hydrogen-like numbering system of the quantum
states can again be used, figure 14.14, with one
difference. For hydrogen, a given energy level  allows all orbital
momentum quantum numbers
allows all orbital
momentum quantum numbers  up to
up to  . For nuclei,
. For nuclei,  must
be even if
must
be even if  is odd and vice-versa, chapter 14.12.1. Also,
while for the (nonrelativistic) hydrogen atom the energy does not
depend on
is odd and vice-versa, chapter 14.12.1. Also,
while for the (nonrelativistic) hydrogen atom the energy does not
depend on  , for nuclei that is only a rough approximation.
(It assumes that the nuclear potential is like an harmonic oscillator
one, and that is really crude.)
, for nuclei that is only a rough approximation.
(It assumes that the nuclear potential is like an harmonic oscillator
one, and that is really crude.)
Table A.2:
More realistic radial integral correction factors for nuclei.
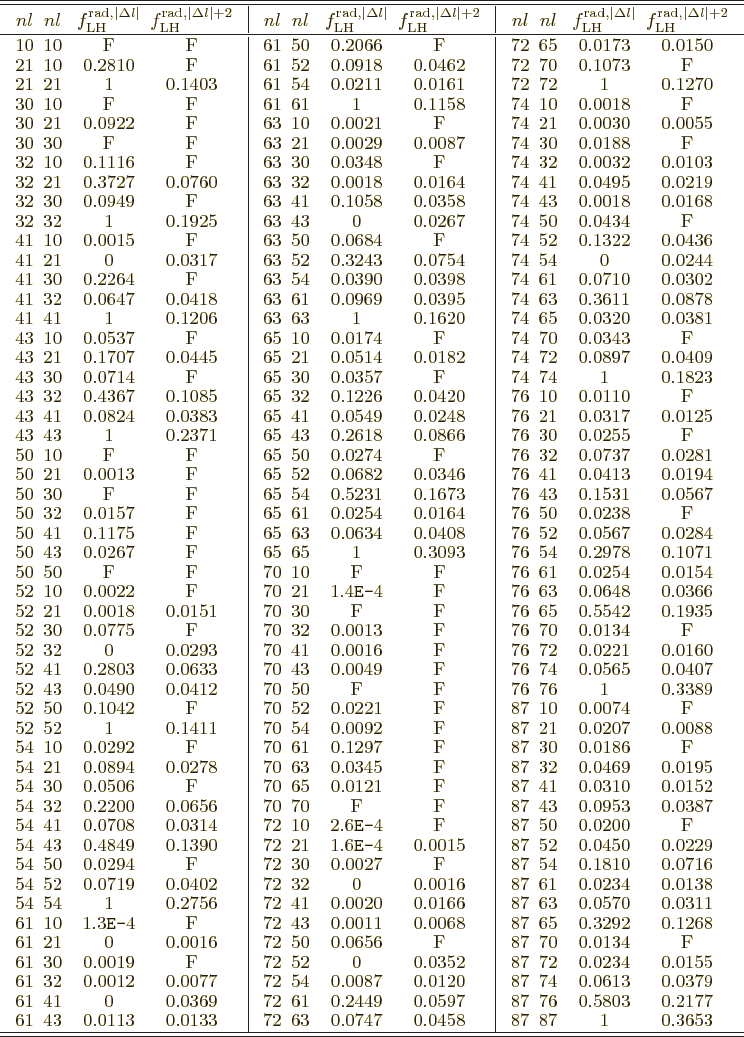 |
Radial factors for the impenetrable-sphere model using this numbering
system are given in table A.2.
These results illustrate the limitations of  transitions in
the single-particle model. Because of the condition (A.186)
above and parity, the orbital quantum number
transitions in
the single-particle model. Because of the condition (A.186)
above and parity, the orbital quantum number  cannot change in
cannot change in
 transitions. A glance at the table then shows that the
radial factor is zero unless the initial and final radial states are
identical. (That is a consequence of the orthonormality of the energy
states.) So
transitions. A glance at the table then shows that the
radial factor is zero unless the initial and final radial states are
identical. (That is a consequence of the orthonormality of the energy
states.) So  transitions cannot change the radial state.
All they can do is change the direction of the orbital angular
momentum or spin of a given state. Obviously that is ho-hum, though
with a spin-orbit term it may still do something. Without a
spin-orbit term, there would be no energy change, and Fermi’s
golden rule would make the theoretical transition rate then zero.
That is similar to the limitation of
transitions cannot change the radial state.
All they can do is change the direction of the orbital angular
momentum or spin of a given state. Obviously that is ho-hum, though
with a spin-orbit term it may still do something. Without a
spin-orbit term, there would be no energy change, and Fermi’s
golden rule would make the theoretical transition rate then zero.
That is similar to the limitation of  transitions for the
nonrelativistic hydrogen atom in chapter 7.4.4.
transitions for the
nonrelativistic hydrogen atom in chapter 7.4.4.
It may be instructive to use the more realistic radial factors of
table A.2 to get a rough idea of the errors in the
Weisskopf ones. The initial comparison will be restricted to changes
in the principal quantum number of no more than one unit. That means
that transitions between widely separated shells will be ignored.
Also, only the lowest possible multipole level will be considered.
That corresponds to the first of each pair of values in the table.
Assuming an electric transition,  is the difference between the
is the difference between the
 values in the table. Consider now the following two simple
approximations of the radial factor:
values in the table. Consider now the following two simple
approximations of the radial factor:
 |
(A.187) |
The coefficient 1.5 comes from a least square approximation of the
data. For  transitions, the exact value 1 should be used.
transitions, the exact value 1 should be used.
For the given data, it turns out that the Weisskopf estimate is on
average too large by a factor 5. In the worst case, the Weisskopf
estimate is too large by a factor 18. The empirical formula is on
average off by a factor 2, and in the worst case by a factor 4.
If any arbitrary change in principal quantum number is allowed, the
possible errors are much larger. In that case the Weisskopf estimates
are off by average factor of 20, and a maximum factor of 4 000. The
empirical estimates are off by an average factor of 8, and a maximum
one of 1 000. Including the next number in table A.2
does not make much of a difference here.
These errors do depend on the change in principal quantum numbers.
For changes in principal quantum number no larger than 2 units, the
empirical estimate is off by a factor no greater that 10. For 3 or 4
unit changes, the estimate is off by a factor no greater than about
100. The absolute maximum error factor of 1 000 occurs for a 5 unit
change in the principal quantum number. For the Weiskopf estimate,
multiply these maximum factors by 4.
These data exclude the  transitions mentioned earlier, for
which the radial factor is either 0 or 1 exactly. The value 0 implies
an infinite error factor for a Weisskopf-type estimate of the radial
factor. But that requires an
transitions mentioned earlier, for
which the radial factor is either 0 or 1 exactly. The value 0 implies
an infinite error factor for a Weisskopf-type estimate of the radial
factor. But that requires an 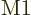 transition with at least a
two unit change in the principal quantum number. In other words, it
requires an
transition with at least a
two unit change in the principal quantum number. In other words, it
requires an 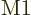 transition with a huge energy change.
transition with a huge energy change.
Consider now the angular factor in the decay rates (A.184)
and (A.185). It arises from integrating the spherical
harmonics, (A.183). But the actual angular factor really
used in the transition rates (A.184) and (A.185)
also involves an averaging over the possible angular orientations of
the initial atom. (This orientation is reflected in its magnetic
quantum number 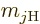 .) And it involves a summation
over the different angular orientations of the final nucleus that can
be decayed to. The reason is that experimentally, there is usually no
control over the orientation of the initial and final nuclei. An
average initial nucleus will have an average orientation. But each
final orientation that can be decayed to is a separate decay process,
and the decay rates add up. (The averaging over the initial
orientations does not really make a difference; all orientations decay
at the same rate, since space has no preferred direction. The
summation over the final orientations is critical.)
.) And it involves a summation
over the different angular orientations of the final nucleus that can
be decayed to. The reason is that experimentally, there is usually no
control over the orientation of the initial and final nuclei. An
average initial nucleus will have an average orientation. But each
final orientation that can be decayed to is a separate decay process,
and the decay rates add up. (The averaging over the initial
orientations does not really make a difference; all orientations decay
at the same rate, since space has no preferred direction. The
summation over the final orientations is critical.)
Table A.3:
Angular integral
correction factors
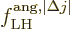 and
and
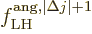 for the Weisskopf electric unit and the Moszkowski magnetic one.
The correction for the Weisskopf magnetic unit is to cross it out
and write in the Moszkowski unit.
for the Weisskopf electric unit and the Moszkowski magnetic one.
The correction for the Weisskopf magnetic unit is to cross it out
and write in the Moszkowski unit.
![\begin{table}\begin{displaymath}
{
\setlength{\arraycolsep}{2.7pt}
\begin{arr...
...[5pt]
% end weisfc2
\hline\hline
\end{array}}
\end{displaymath}
\end{table}](img4910.gif) |
Values for the angular factor are in table A.3. For the
first and second number of each pair respectively:
More generally, the angular factor is given by,
[33, p. 878],
![\begin{displaymath}
\fbox{$\displaystyle
f^{\rm ang,\ell}_{\rm LH} = (2j_{\rm{...
...56ex\hbox{\the\scriptfont0 2}\kern.05em\right\rangle}]^2
$} %
\end{displaymath}](img4912.gif) |
(A.188) |
Here the quantity in square brackets is called a Clebsch-Gordan
coefficient. For small angular momenta, values can be found in figure
12.5. For larger values, refer to {N.13}. The
leading factor is the reason that the values in the table are not the
same if you swap the initial and final states. When the final state
has the higher angular momentum, there are more nuclear orientations
that an atom can decay to.
It may be noted that [11, p. 9-178] gives the above
factor for electric transitions as
Here the array in parentheses is the so-called Wigner 3j symbol and
the one in curly brackets is the Wigner 6j symbol, {N.13}.
The idea is that this expression will take care of the selection rules
automatically. And so it does, if you assume that the
multiply-defined  is
is  , as the author seems to say. Of
course, selection rules might be a lot easier to evaluate than 3j and
6j symbols.
, as the author seems to say. Of
course, selection rules might be a lot easier to evaluate than 3j and
6j symbols.
For magnetic multipole transitions, with 



 , the
same source comes up with
, the
same source comes up with
Here the final array in curly brackets is the Wigner 9j symbol. The
bad news is that the 6j symbol does not allow any transitions of
lowest multipole order to occur! Someone familiar with 6j symbols can
immediately see that from the so-called triangle inequalities that the
coefficients of 6j symbols must satisfy, {N.13}.
Fortunately, it turns out that if you simply leave out the 6j symbol,
you do seem to get the right values and selection rules.
The magnetic multipole matrix element also involves an angular
momentum factor. This factor turns out to be relatively simple,
{D.43.3}:
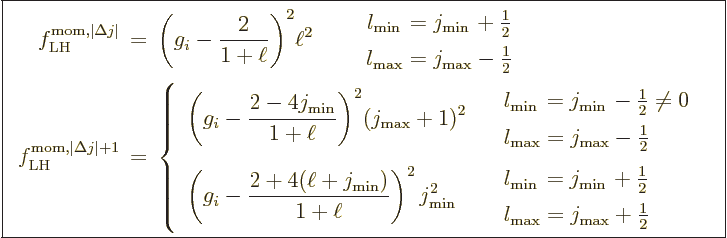 |
(A.189) |
Here min” and “max
refer to whatever is
the smaller, respectively larger, one of the initial and final values.
The stated values of the orbital angular momentum  are the only
ones allowed by parity and the orbital angular momentum conservation
condition (A.186). In particular, consider the first
expression above, for the minimum multipole order
are the only
ones allowed by parity and the orbital angular momentum conservation
condition (A.186). In particular, consider the first
expression above, for the minimum multipole order 

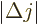 . According to this expression, the change in
orbital angular momentum cannot exceed the change in net angular
momentum. That forbids a lot of magnetic transitions in a shell model
setting, transitions that seem perfectly fine if you only look at net
angular momentum and parity. Add to that the earlier observation that
. According to this expression, the change in
orbital angular momentum cannot exceed the change in net angular
momentum. That forbids a lot of magnetic transitions in a shell model
setting, transitions that seem perfectly fine if you only look at net
angular momentum and parity. Add to that the earlier observation that
 transitions cannot change the radial state at all.
Magnetic transitions are quite handicapped according to the
single-particle model used here.
transitions cannot change the radial state at all.
Magnetic transitions are quite handicapped according to the
single-particle model used here.
Of course, a single-particle model is not exact for multiple-particle
systems. In a more general setting, transitions that in the ideal
model would violate the orbital angular momentum condition can occur.
For example, consider the possibility that the true state picks up
some uncertainty in orbital angular momentum.
Presumably such transitions would be unexpectedly slow compared to
transitions that do not violate any approximate orbital angular
momentum conditions. That makes estimating the magnetic transition
rates much more tricky. After all, for nuclei the net angular
momentum is usually known with some confidence, but the orbital
angular momentum of individual nucleons is not.
Fortunately, for electric transitions orbital angular momentum
conservation does not provide additional limitations. Here the
orbital requirements are already satisfied if net angular momentum and
parity are conserved.
The derived decay estimates are now used to define standard decay
rates. It is assumed that the multipole order is minimal, 

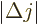 , and that the final angular momentum is
, and that the final angular momentum is
 . As table A.3 shows, that makes the
angular factor equal to 1. The standard electric decay rate is then
. As table A.3 shows, that makes the
angular factor equal to 1. The standard electric decay rate is then
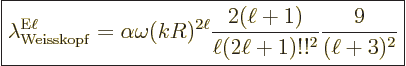 |
(A.190) |
This decay rate is called the “Weisskopf unit” for electric multipole transitions.
It is commonly indicated by W.u.
Measured actual decay rates are compared to this unit to get an idea
whether they are unusually high or low.
Note that the decay rates are typically orders of magnitude off the
mark. That is due to effects that cannot be accounted for. Nucleons
are not independent particles by far. And even if they were, their
radial wave functions would not be constant. The used expression for
the electric matrix element is probably no good, {N.14}.
And especially higher multipole orders depend very sensitively on the
nuclear radius, which is imprecisely defined.
The standard magnetic multipole decay rate becomes under the same
assumptions:
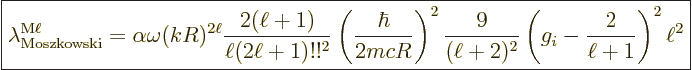 |
(A.191) |
This decay rate is called the “Moszkowski unit” for magnetic multipole transitions.
Finally, it should be mentioned that it is customary to ballpark the
final momentum factor in the Moszkowski unit by 40. That is because
Jesus spent 40 days in the desert. Also, the factor  is
customarily replaced by
is
customarily replaced by 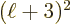 ,
[10, p. 9-49], [36, p. 676],
[5, p. 242], because, hey, anything for a laugh. Other
sources keep the
,
[10, p. 9-49], [36, p. 676],
[5, p. 242], because, hey, anything for a laugh. Other
sources keep the  factor just like it is,
[11, p. 9-178], [31, p. 332], because,
hey, why not? Note that the Handbook of Physics does both, depending
on the author you look at. Taking the most recent of the cited
sources, as well as [[4]], as reference the new and improved
magnetic transition rate may be:
factor just like it is,
[11, p. 9-178], [31, p. 332], because,
hey, why not? Note that the Handbook of Physics does both, depending
on the author you look at. Taking the most recent of the cited
sources, as well as [[4]], as reference the new and improved
magnetic transition rate may be:
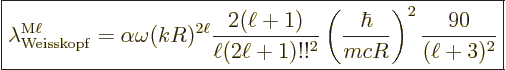 |
(A.192) |
This is called the Weisskopf magnetic unit. Note that the humor
factor has been greatly increased. Whether there is a 2 or 3 in the
final fraction does not make a difference. All analysis is relative
to the perception of the observer. Where one perceives a 2 another
sees a 3. Everthing is relative, as Einstein supposedly said, and
otherwise quantum mechanics definitely did.
Note that the Weisskopf magnetic unit looks exactly like the electric
one, except for the addition of a zero and the additional fraction
between parentheses. That makes it easier to remember, especially for
those who can remember the electric unit. For them the savings in
time is tremendous, because they do not have to look up the correct
expression. That can save a lot of time because many standard
references have the formulae wrong or in some weird system of units.
All that time is much better spend trying to guess whether your
source, or your editor, uses a 2 or a 3.
A.25.9 Errors in other sources
There is a notable amount of errors in descriptions of the Weisskopf
and Moszkowski estimates found elsewhere. That does not even
include not mentioning that the electric multipole rate is likely no
good, {N.14}. Or randomly using  or
or  in
the Weisskopf magnetic unit.
in
the Weisskopf magnetic unit.
These errors are more basic. The first edition of the Handbook of
Physics, [10, p. 9-49], gives both Weisskopf
units wrong. Squares are missing on the  , and so is the
fine structure constant. The other numerical factors are consistent
between the two units, but not right. Probably a strangely normalized
matrix element is given, rather than the stated decay rates
, and so is the
fine structure constant. The other numerical factors are consistent
between the two units, but not right. Probably a strangely normalized
matrix element is given, rather than the stated decay rates
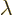 , and in addition the square was forgotten.
, and in addition the square was forgotten.
The same Handbook, [10, p. 9-110], but a different
author, uses 
 2 instead of
2 instead of  in the Moszkowski estimate.
(Even physicists themselves can get confused if sometimes you define
in the Moszkowski estimate.
(Even physicists themselves can get confused if sometimes you define
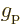 to be 5.6 and sometimes 2.8, which also happens to be the
magnetic moment
to be 5.6 and sometimes 2.8, which also happens to be the
magnetic moment 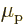 in nuclear magnetons, which is often
used as a
in nuclear magnetons, which is often
used as a nondimensional
unit where 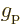 is
really needed, etcetera.) More seriously, this error is carried over
to the given plot of the Moszkowski unit, which is therefore wrong.
Which is in addition to the fact that the nuclear radius used in it is
too large by modern standards, using 1.4 rather than 1.2 in
(A.177).
is
really needed, etcetera.) More seriously, this error is carried over
to the given plot of the Moszkowski unit, which is therefore wrong.
Which is in addition to the fact that the nuclear radius used in it is
too large by modern standards, using 1.4 rather than 1.2 in
(A.177).
The error is corrected in the second edition,
[11, p. 9-178], but the Moszkowski plot has
disappeared. In favor of the Weisskopf magnetic unit, of course.
Think of the scientific way in which the Weisskopf unit has been
deduced! This same reference also gives the erroneous angular factor
for magnetic transitions mentioned in the previous subsection. Of
course an additional 6j symbol that sneaks in is easily overlooked.
No serious errors were observed in [33]. (There is a
readily-fixed error in the conversion formula for when the initial and
final states are swapped.) This source does not list the Weisskopf
magnetic unit. (Which is certainly defensible in view of its
nonsensical assumptions.) Unfortunately non-SI units are used.
The electric dipole matrix element in [36, p. 676]
is missing a factor 1/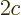 . The claim that this element can be
found by
. The claim that this element can be
found by straightforward calculation
is ludicrous.
Not only is the mathematics convoluted, it also involves the major
assumption that the potentials depend only on position. A square is
missing in the Moszkowski unit, and the table of corresponding widths
are in eV instead of the stated 1/s.
All three units are given incorrectly in [31, p. 332].
There is a factor 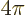 in them that should not be there. And the
magnetic rate is missing a factor
in them that should not be there. And the
magnetic rate is missing a factor  . The constant in the
numerical expression for
. The constant in the
numerical expression for 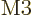 transitions should be 15, not 16.
Of course, the difference is negligible compared to replacing the
parenthetical expression by 40, or compared to the orders of magnitude
that the estimate is commonly off anyway.
transitions should be 15, not 16.
Of course, the difference is negligible compared to replacing the
parenthetical expression by 40, or compared to the orders of magnitude
that the estimate is commonly off anyway.
The Weisskopf units are listed correctly in
[5, p. 242]. Unfortunately non-SI units are used. The
Moszkowski unit is not mentioned. The nonsensical nature of the
Weisskopf magnetic unit is not pointed out. Instead it is claimed
that it is found by a similar calculation as the electric unit.
![]() .
.![]() .
.![]()
![]() :
:![]()
![]()
![]() .
.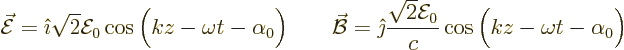
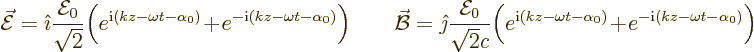
![]() ,
,![]()
![]() .
.![]()
![]()
![]()
![]() ,
,![]() ,
,![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 3
3![]()
![\begin{displaymath}
H_{21,i} = {\left\langle\psi_{\rm {L}}\hspace{0.3pt}\right\...
...i{\widehat S}_{i,y})]
{\left\vert\psi_{\rm {H}}\right\rangle}
\end{displaymath}](img4793.gif)

![\begin{displaymath}
H = H_0 + \sum_i \left[-\frac{q_i}{m_i}\skew3\vec A_i\cdot ...
...\skew2\vec{\cal B}_i \cdot {\skew 6\widehat{\vec S}}_i \right]
\end{displaymath}](img4804.gif)
![]()
![]()
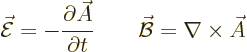

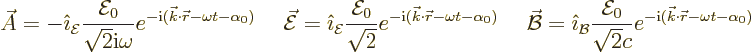
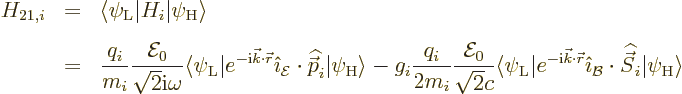
![]() -
-![]() -
-![]() .
.![]()

![]() ,
,![]() .
.![]()
![]() .
.![]()
![]()
![]()
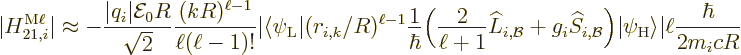
![]() .
.
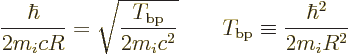
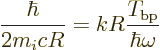
![]()
![]()
![]()
![]() -
-![]() -
-![]() .
.![]() 1
1![]()
![]()
![]()
![]()
![]() .
.![]() 0
0![]() 5
5![]()
![]()
![]()
![]()
![]() 1
1![]() 1
1![]() ,
,![]()
![]()
![]()
![]() -
-![]()
![]()
![]() ,
,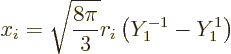
![]()
![]() .
.![]()
![]()
![]()
![]() .
.![]()
![]() .
.![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]() -
-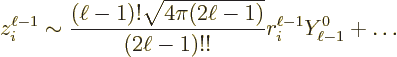
![]() ,
,![]() -
-![]()
![]() .
.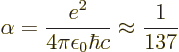
![]()
![]()
![]()
![]()
![]()
![]()
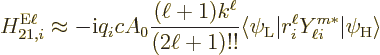
![]()
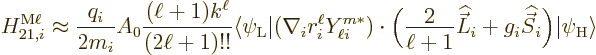
![]()
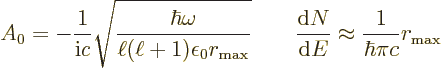
![]() .
.![]()
![]()
![]()
![]()
![]() -
-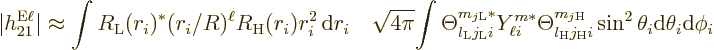
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]() .
.![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![\begin{table}\begin{displaymath}
{
\setlength{\arraycolsep}{2.7pt}
\begin{arr...
...[5pt]
% end weisfc2
\hline\hline
\end{array}}
\end{displaymath}
\end{table}](img4910.gif)
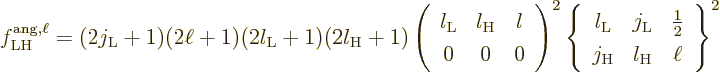
![]()
![]()
![]()
![]()
![]() ,
,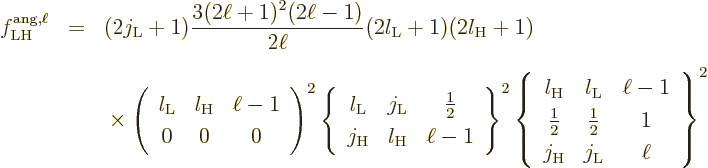
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]() ,
,![]() .
.![]()
![]() ,
,![]()
![]()
![]()
![]() ,
,![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]() .
.![]()