| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
12.3 Ladders
This section starts the quest to figure out everything that the
fundamental commutation relations mean for angular momentum. It will
first be verified that any angular momentum can always be described
using 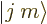 eigenstates with definite values of square angular
momentum
eigenstates with definite values of square angular
momentum 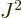 and
and  angular momentum
angular momentum 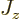 . Then it will be
found that these angular momentum states occur in groups called
. Then it will be
found that these angular momentum states occur in groups called
ladders
.
To start with the first one, the mathematical condition for a complete
set of eigenstates 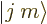 to exist is that the angular momentum
operators
to exist is that the angular momentum
operators  and
and 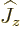 commute. They do; using the commutator
manipulations of chapter 4.5.4), it is easily found
that:
commute. They do; using the commutator
manipulations of chapter 4.5.4), it is easily found
that:
So mathematics says that eigenstates 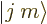 of
of 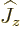 and
and
 exist satisfying
exist satisfying
and that are complete in the sense that any state can be described in
terms of these 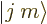 .
.
Unfortunately the eigenstates 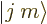 , except for
, except for 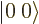 states, do not satisfy relations like (12.2) for
states, do not satisfy relations like (12.2) for  or
or
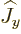 . The problem is that
. The problem is that  and
and 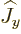 do not commute
with
do not commute
with 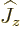 . But
. But  and
and 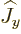 do commute with
do commute with
 , and you might wonder if that is still worth something.
To find out, multiply, say, the zero commutator
, and you might wonder if that is still worth something.
To find out, multiply, say, the zero commutator ![$[{\widehat J}^2,{\widehat J}_x]$](img2646.gif) by
by
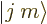 :
:
Now take the second term to the right hand side of the equation,
noting that 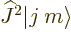

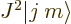 with
with 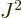 just a number that can
be moved up-front, to get:
just a number that can
be moved up-front, to get:
Looking a bit closer at this equation, it shows that the combination
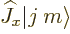 satisfies the same eigenvalue problem for
satisfies the same eigenvalue problem for  as
as
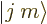 itself. In other words, the multiplication by
itself. In other words, the multiplication by  does
not affect the square angular momentum
does
not affect the square angular momentum 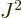 at all.
at all.
To be picky, that is not quite true if 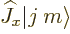 would be zero,
because zero is not an eigenstate of anything. However, such a thing
only happens if there is no angular momentum; (it would make
would be zero,
because zero is not an eigenstate of anything. However, such a thing
only happens if there is no angular momentum; (it would make 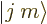 an eigenstate of
an eigenstate of  with eigenvalue zero in addition to an
eigenstate of
with eigenvalue zero in addition to an
eigenstate of 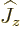 {D.63}). Except for that trivial case,
{D.63}). Except for that trivial case,
 does not affect square angular momentum. And neither does
does not affect square angular momentum. And neither does
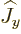 or any combination of the two.
or any combination of the two.
Angular momentum in the  -direction is affected by
-direction is affected by  and
by
and
by 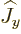 , since they do not commute with
, since they do not commute with 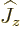 like they do
with
like they do
with  . Nor is it possible to find any linear combination
of
. Nor is it possible to find any linear combination
of  and
and 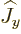 that does commute with
that does commute with 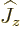 . What is the
next best thing? Well, it is possible to find two
combinations, to wit
. What is the
next best thing? Well, it is possible to find two
combinations, to wit
 |
(12.4) |
that satisfy the “commutator eigenvalue problems”:
These two turn out to be quite remarkable operators.
Like  and
and 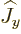 , their combinations
, their combinations 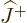 and
and 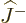 leave
leave 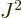 alone. To examine what the operator
alone. To examine what the operator 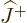 does with the
linear momentum in the
does with the
linear momentum in the  -direction, multiply its commutator relation
above by an eigenstate
-direction, multiply its commutator relation
above by an eigenstate 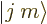 :
:
Or, taking the second term to the right hand side of the equation and
noting that by definition 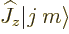

 ,
,
That is a stunning result, as it shows that 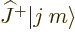 is an
eigenstate with
is an
eigenstate with  angular momentum
angular momentum 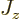

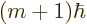 instead
of
instead
of 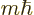 . In other words,
. In other words, 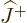 adds exactly one unit
adds exactly one unit
 to the
to the  angular momentum, turning an
angular momentum, turning an 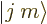 state into a
state into a
 one!
one!
Figure 12.1:
Example bosonic ladders.
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\resizebox{5.6truein}{...
...of\\ [-4pt]
\strut a graviton?}}}
\end{picture}}
\end{picture}}
\end{figure}](img2663.gif) |
Figure 12.2:
Example fermionic ladders.
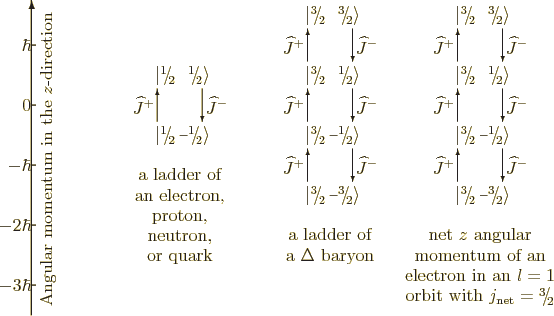 |
If you apply  another time, you get a state of still higher
another time, you get a state of still higher
 angular momentum
angular momentum 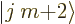 , and so on, like the
rungs on a ladder. This is graphically illustrated for some examples
in figures 12.1 and 12.2. The process
eventually comes to an halt at some top rung
, and so on, like the
rungs on a ladder. This is graphically illustrated for some examples
in figures 12.1 and 12.2. The process
eventually comes to an halt at some top rung 

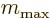 where
where 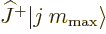
 0. It has to, because the
angular momentum in the
0. It has to, because the
angular momentum in the  -direction cannot just keep growing
forever: the square angular momentum in the
-direction cannot just keep growing
forever: the square angular momentum in the  -direction only must
stay less than the total square angular momentum in all three
directions {N.27}.
-direction only must
stay less than the total square angular momentum in all three
directions {N.27}.
The second ladder operator
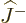 works in much the
same way, but it goes down the ladder; its deducts one unit
works in much the
same way, but it goes down the ladder; its deducts one unit  from the angular momentum in the
from the angular momentum in the  -direction at each application.
-direction at each application.
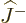 provides the second stile to the ladders, and must terminate at
some bottom rung
provides the second stile to the ladders, and must terminate at
some bottom rung 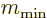 .
.
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() .
.![]()
![]()
![]() .
.![]()
![]()
![]() ,
,![]()
![]() :
:![]()
![]()
![]()
![]()
![]()
![]()
![]() -
-![]()
![]() ,
,![]()
![]() .
.![]()
![]()
![]() .
.![]()
![]() ,
,![]()
![]()
![]()
![]()
![]() -
-![]() :
:![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]() -
-![]() -
-![]()
![]()
![]() -
-![]()
![]() .
.