| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
12.4 Possible values of angular momentum
The fact that the angular momentum ladders of the previous section
must have a top and a bottom rung restricts the possible values that
angular momentum can take. This section will show that the azimuthal
quantum number  can either be a nonnegative whole number or half of
one, but nothing else. And it will show that the magnetic quantum
number
can either be a nonnegative whole number or half of
one, but nothing else. And it will show that the magnetic quantum
number  must range from
must range from 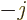 to
to 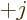 in unit increments. In other
words, the bosonic and fermionic example ladders in figures
12.1 and 12.2 are representative of all that
is possible.
in unit increments. In other
words, the bosonic and fermionic example ladders in figures
12.1 and 12.2 are representative of all that
is possible.
To start, in order for a ladder to end at a top rung
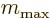 ,
, 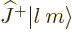 has to be zero for
has to be zero for 

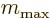 . More specifically, its magnitude
. More specifically, its magnitude
 must be zero. The square magnitude is
given by the inner product with itself:
must be zero. The square magnitude is
given by the inner product with itself:
Now because of the complex conjugate that is used in the left hand
side of an inner product, (see chapter 2.3), 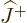

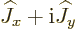 goes to the other side of the product as
goes to the other side of the product as 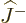

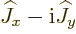 , and you must have
, and you must have
That operator product can be multiplied out:
but  is the square angular momentum
is the square angular momentum  except for
except for
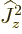 , and the term within the parentheses is the commutator
, and the term within the parentheses is the commutator
![$[{\widehat J}_x,{\widehat J}_y]$](img2680.gif) which is according to the fundamental commutation
relations equal to
which is according to the fundamental commutation
relations equal to  , so
, so
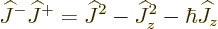 |
(12.5) |
The effect of each of the operators in the left hand side on a state
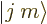 is known and the inner product can be figured out:
is known and the inner product can be figured out:
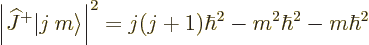 |
(12.6) |
The question where angular momentum ladders end can now be answered:
There are two possible solutions to this quadratic equation for
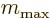 , to wit
, to wit 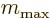

 or
or
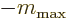

 . The second solution is impossible
since it already would have the square
. The second solution is impossible
since it already would have the square  angular momentum exceed the
total square angular momentum. So unavoidably,
angular momentum exceed the
total square angular momentum. So unavoidably,
That is one of the things this section was supposed to show.
The lowest rung on the ladder goes the same way; you get
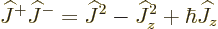 |
(12.7) |
and then
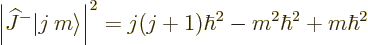 |
(12.8) |
and the only acceptable solution for the lowest rung on the ladders is
It is nice and symmetric; ladders run from 


 up to
up to 

 , as the examples in figures 12.1 and
12.2 already showed.
, as the examples in figures 12.1 and
12.2 already showed.
And in fact, it is more than that; it also limits what the quantum
numbers  and
and  can be. For, since each step on a ladder
increases the magnetic quantum number
can be. For, since each step on a ladder
increases the magnetic quantum number  by one unit, you have
for the total number of steps up from bottom to top:
by one unit, you have
for the total number of steps up from bottom to top:
But the number of steps is a whole number, and so the azimuthal
quantum  must either be a nonnegative integer, such as 0, 1, 2,
..., or half of one, such as
must either be a nonnegative integer, such as 0, 1, 2,
..., or half of one, such as 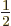 ,
,  ,
...
,
...
Integer  values occur, for example, for the spherical harmonics of
orbital angular momentum and for the spin of bosons like photons.
Half-integer values occur, for example, for the spin of fermions such
as electrons, protons, neutrons, and
values occur, for example, for the spherical harmonics of
orbital angular momentum and for the spin of bosons like photons.
Half-integer values occur, for example, for the spin of fermions such
as electrons, protons, neutrons, and  particles.
particles.
Note that if  is a half-integer, then so are the corresponding
values of
is a half-integer, then so are the corresponding
values of  , since
, since  starts from
starts from 
 and increases in
unit steps. See again figures 12.1 and 12.2
for some examples. Also note that ladders terminate just before
and increases in
unit steps. See again figures 12.1 and 12.2
for some examples. Also note that ladders terminate just before
 -momentum would exceed total momentum.
-momentum would exceed total momentum.
It may also be noted that ladders are distinct. It is not possible to
go up one ladder, like the first 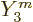 one in figure
12.1 with
one in figure
12.1 with 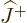 and then come down the second one using
and then come down the second one using
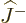 . The reason is that the states
. The reason is that the states 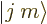 are eigenstates
of the operators
are eigenstates
of the operators 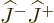 , (12.5), and
, (12.5), and
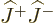 , (12.7), so going up with
, (12.7), so going up with 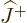 and then
down again with
and then
down again with 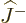 , or vice-versa, returns to the same
state. For similar reasons, if the tops of two ladders are
orthonormal, then so is the rest of their rungs.
, or vice-versa, returns to the same
state. For similar reasons, if the tops of two ladders are
orthonormal, then so is the rest of their rungs.
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]() -
-![]()
![]()
![]() .
.![]()
![]() ,
,![]() ,
,![]()
![]() ,
,