10.6 Nearly-Free Elec­trons

The free-elec­tron en­ergy spec­trum does not have bands. Bands only form when some of the forces that the am­bi­ent solid ex­erts on the elec­trons are in­cluded. In this sec­tion, some of the me­chan­ics of that process will be ex­plored. The only force con­sid­ered will be one given by a pe­ri­odic lat­tice po­ten­tial. The dis­cus­sion will still ig­nore true elec­tron-elec­tron in­ter­ac­tions, time vari­a­tions of the lat­tice po­ten­tial, lat­tice de­fects, etcetera.

In ad­di­tion, to sim­plify the math­e­mat­ics it will be as­sumed that the lat­tice po­ten­tial is weak. That makes the ap­proach here di­a­met­ri­cally op­po­site to the one fol­lowed in the dis­cus­sion of the one-di­men­sion­al crys­tals. There the start­ing point was elec­trons tightly bound to widely spaced atoms; the atom en­ergy lev­els then cor­re­sponded to in­fi­nitely con­cen­trated bands that fanned out when the dis­tance be­tween the atoms was re­duced. Here the start­ing idea is free elec­trons in closely packed crys­tals for which the bands are com­pletely fanned out so that there are no band gaps left. But it will be seen that when a bit of non­triv­ial lat­tice po­ten­tial is added, en­ergy gaps will ap­pear.

The analy­sis will again be based on the Flo­quet en­ergy eigen­func­tions for the elec­trons. As noted in the pre­vi­ous sec­tion, they cor­re­spond to pe­ri­odic bound­ary con­di­tions for pe­ri­ods $2\ell_x$, $2\ell_y$, and $2\ell_z$. In case that the en­ergy eigen­func­tions for con­fined elec­trons are de­sired, they can be ob­tained from the Bloch so­lu­tions to be de­rived in this sec­tion in the fol­low­ing way: Take a Bloch so­lu­tion and flip it over around the $x$ $\vphantom0\raisebox{1.5pt}{$=$}$ 0 plane, i.e. re­place $x$ by $\vphantom{0}\raisebox{1.5pt}{$-$}$$x$. Sub­tract that from the orig­i­nal so­lu­tion, and you have a so­lu­tion that is zero at $x$ $\vphantom0\raisebox{1.5pt}{$=$}$ 0. And be­cause of pe­ri­od­ic­ity and odd sym­me­try, it will also be zero at $x$ $\vphantom0\raisebox{1.5pt}{$=$}$ $\ell_x$. Re­peat these steps in the $y$ and $z$ di­rec­tions. It will pro­duce en­ergy eigen­func­tions for elec­trons con­fined to a box 0 $\raisebox{.3pt}{$<$}$ $x$ $\raisebox{.3pt}{$<$}$ $\ell_x$, 0 $\raisebox{.3pt}{$<$}$ $y$ $\raisebox{.3pt}{$<$}$ $\ell_y$, 0 $\raisebox{.3pt}{$<$}$ $z$ $\raisebox{.3pt}{$<$}$ $\ell_z$. This method works as long as the lat­tice po­ten­tial has enough sym­me­try that it does not change dur­ing the flip op­er­a­tions.

Fig­ure 10.20: The red dot shows the wavenum­ber vec­tor of a sam­ple free elec­tron wave func­tion. It is to be cor­rected for the lat­tice po­ten­tial.

The ap­proach will be to start with the so­lu­tions for force-free elec­trons and see how they change if a small, but nonzero lat­tice po­ten­tial is added to the mo­tion. It will be a “nearly-free elec­tron model.” Con­sider a sam­ple Flo­quet wave num­ber as shown by the red dot in the wave num­ber space fig­ure 10.20. If there is no lat­tice po­ten­tial, the cor­re­spond­ing en­ergy eigen­func­tion is the free-elec­tron one,

$$\pp{{\vec k},0}//// = \frac{1}{\sqrt{8\ell_x\ell_y\ell_z}} e^{{\rm i}(k_x x + k_y y + k_z z)}$$

where the sub­script zero merely in­di­cates that the lat­tice po­ten­tial is zero. (This sec­tion will use the ex­tended zone scheme be­cause it is math­e­mat­i­cally eas­i­est.) If there is a lat­tice po­ten­tial, the eigen­func­tion will change into a Bloch one of the form

$$\pp{{\vec k}}//// = \pp{{\rm p},{\vec k}}//// e^{{\rm i}(k_x x + k_y y + k_z z)}$$

where $\pp{{\rm {p}},{\vec k}}////$ is pe­ri­odic on an atomic scale. If the lat­tice po­ten­tial is weak, as as­sumed here,

$$\pp{{\rm p},{\vec k}}//// \approx \frac{1}{\sqrt{8\ell_x\ell_y\ell_z}}$$

Also, the en­ergy will be al­most the free-elec­tron one:

$${\vphantom' E}^{\rm e}_{\vec k}\approx {\vphantom' E}^{\rm e}_{{\vec k},0} = \frac{\hbar^2}{2m_{\rm e}} k^2$$

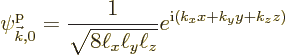
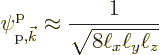
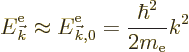
How­ever, that is not good enough. The in­ter­est here is in the changes in the en­ergy due to the lat­tice po­ten­tial, even if they are weak. So the first thing will be to fig­ure out these en­ergy changes.

10.6.1 En­ergy changes due to a weak lat­tice po­ten­tial

Find­ing the en­ergy changes due to a small change in a Hamil­ton­ian can be done by a math­e­mat­i­cal tech­nique called “per­tur­ba­tion the­ory.” A full de­scrip­tion and de­riva­tion are in {A.38} and {D.79}. This sub­sec­tion will sim­ply state the needed re­sults.

The ef­fects of a small change in a Hamil­ton­ian, here be­ing the weak lat­tice po­ten­tial, are given in terms of the so-called Hamil­ton­ian per­tur­ba­tion co­ef­fi­cients de­fined as

$$H_{{\vec k}\underline{\vec k}} \equiv \langle\pp{{\vec k},0}////\vert V\pp{\underline{\vec k},0}////\rangle$$ (10.13)

where $V$ is the lat­tice po­ten­tial, and the $\pp{{\vec k},0}////$ are the free-elec­tron en­ergy eigen­func­tions.

In those terms, the en­ergy of the eigen­func­tion $\psi_{\vec k}$ with Flo­quet wave num­ber ${\vec k}$ is

$${\vphantom' E}^{\rm e}_{\vec k}\approx {\vphantom' E}^{\rm ... ...ne{\vec k},0}-{\vphantom' E}^{\rm e}_{{\vec k},0}} + \ldots %$$ (10.14)

Here ${\vphantom' E}^{\rm e}_{{\vec k},0}$ is the free-elec­tron en­ergy. The dots stand for con­tri­bu­tions that can be ig­nored for suf­fi­ciently weak po­ten­tials.

The first cor­rec­tion to the free-elec­tron en­ergy is the Hamil­ton­ian per­tur­ba­tion co­ef­fi­cient $H_{{\vec k}{\vec k}}$. How­ever, by writ­ing out the in­ner prod­uct, it is seen that this per­tur­ba­tion co­ef­fi­cient is just the av­er­age lat­tice po­ten­tial. Such a con­stant en­ergy change is of no par­tic­u­lar phys­i­cal in­ter­est; it can be elim­i­nated by re­defin­ing the zero level of the po­ten­tial en­ergy.

Fig­ure 10.21: The grid of nonzero Hamil­ton­ian per­tur­ba­tion co­ef­fi­cients and the prob­lem sphere in wave num­ber space.

That makes the sum in (10.14) the phys­i­cally in­ter­est­ing change in en­ergy. Now, un­like it seems from the given ex­pres­sion, it is not re­ally nec­es­sary to sum over all free-elec­tron en­ergy eigen­func­tions $\psi_{\underline{\vec k},0}$. The only Hamil­ton­ian per­tur­ba­tion co­ef­fi­cients that are nonzero oc­cur for the $\underline{\vec k}$ val­ues shown in fig­ure 10.21 as blue stars. They are spaced apart by amounts $J$ in each di­rec­tion, where $J$ is the large num­ber of phys­i­cal lat­tice cells in that di­rec­tion. These claims can be ver­i­fied by writ­ing the lat­tice po­ten­tial as a Fourier se­ries and then in­te­grat­ing the in­ner prod­uct. More el­e­gantly, you can use the ob­ser­va­tion from ad­den­dum {A.38.3} that the only eigen­func­tions that need to be con­sid­ered are those with the same eigen­val­ues un­der dis­place­ment over the prim­i­tive vec­tors of the lat­tice. (Since the pe­ri­odic lat­tice po­ten­tial is the same af­ter such dis­place­ments, these dis­place­ment op­er­a­tors com­mute with the Hamil­ton­ian.)

The cor­rect ex­pres­sion for the en­ergy change has there­fore now been iden­ti­fied. There is one caveat in the whole story, though. The above analy­sis is not jus­ti­fied if there are eigen­func­tions $\pp{\underline{\vec k},0}////$ on the grid of blue stars that have the same free-elec­tron en­ergy ${\vphantom' E}^{\rm e}_{{\vec k},0}$ as the eigen­func­tion $\pp{{\vec k},0}////$. You can in­fer the prob­lem from (10.14); you would be di­vid­ing by zero if that hap­pened. You would have to fix the prob­lem by us­ing so-called “sin­gu­lar per­tur­ba­tion the­ory,” which is much more elab­o­rate.

For­tu­nately, since the grid is so widely spaced, the prob­lem oc­curs only for rel­a­tively few en­ergy eigen­func­tions $\pp{\vec k}////$. In par­tic­u­lar, since the free-elec­tron en­ergy ${\vphantom' E}^{\rm e}_{{\vec k},0}$ equals $\hbar^2k^2$$\raisebox{.5pt}{$/$}$​$2m_{\rm e}$, the square mag­ni­tude of $\underline{\vec k}$ would have to be the same as that of ${\vec k}$. In other words, $\underline{\vec k}$ would have to be on the same spher­i­cal sur­face around the ori­gin as point ${\vec k}$. So, as long as the grid has no points other than ${\vec k}$ on the spher­i­cal sur­face, all is OK.

10.6.2 Dis­cus­sion of the en­ergy changes

The pre­vi­ous sub­sec­tion de­ter­mined how the en­ergy changes from the free-elec­tron gas val­ues due to a small lat­tice po­ten­tial. It was found that an en­ergy level ${\vphantom' E}^{\rm e}_{{\vec k},0}$ with­out lat­tice po­ten­tial changes due to the lat­tice po­ten­tial by an amount:

$$\Delta{\vphantom' E}^{\rm e}_{{\vec k}} = - \sum_{\underlin... ...\underline{\vec k},0} - {\vphantom' E}^{\rm e}_{{\vec k},0}} %$$ (10.15)

where the $H_{{\vec k}\underline{\vec k}}$ were co­ef­fi­cients that de­pend on the de­tails of the lat­tice po­ten­tial; ${\vec k}$ was the wave num­ber vec­tor of the con­sid­ered free-elec­tron gas so­lu­tion, shown as a red dot in the wavenum­ber space fig­ure 10.21, $\underline{\vec k}$ was an sum­ma­tion in­dex over the blue grid points of that fig­ure, and ${\vphantom' E}^{\rm e}_{\underline{\vec k},0}$ and ${\vphantom' E}^{\rm e}_{{\vec k},0}$ were pro­por­tional to the square dis­tances from the ori­gin to points $\underline{\vec k}$, re­spec­tively ${\vec k}$. ${\vphantom' E}^{\rm e}_{{\vec k},0}$ is also the en­ergy level of the eigen­func­tion with­out lat­tice po­ten­tial.

The ex­pres­sion above for the en­ergy change is not valid when ${\vphantom' E}^{\rm e}_{\underline{\vec k},0}$ $\vphantom0\raisebox{1.5pt}{$=$}$ ${\vphantom' E}^{\rm e}_{{\vec k},0}$, in which case it would in­cor­rectly give in­fi­nite change in en­ergy. How­ever, it is does ap­ply when ${\vphantom' E}^{\rm e}_{\underline{\vec k},0}$ $\vphantom0\raisebox{1.1pt}{$\approx$}$ ${\vphantom' E}^{\rm e}_{{\vec k},0}$, in which case it pre­dicts un­usu­ally large changes in en­ergy. The con­di­tion ${\vphantom' E}^{\rm e}_{\underline{\vec k},0}$ $\vphantom0\raisebox{1.1pt}{$\approx$}$ ${\vphantom' E}^{\rm e}_{{\vec k},0}$ means that a blue star $\underline{\vec k}$ on the grid in fig­ure 10.21 is al­most the same dis­tance from the ori­gin as the red point ${\vec k}$ it­self.

Fig­ure 10.22: Tear­ing apart of the wave num­ber space en­er­gies.

One case for which this hap­pens is when the wave num­ber vec­tor ${\vec k}$ is right next to one of the bound­aries of the Wigner-Seitz cell around the ori­gin. When­ever a ${\vec k}$ is on the verge of leav­ing this cell, one of its lat­tice points is on the verge of get­ting in. As an ex­am­ple, fig­ure 10.22 shows two neigh­bor­ing states ${\vec k}$ strad­dling the right-hand ver­ti­cal plane of the cell, as well as their lat­tice $\underline{\vec k}$ val­ues that cause the un­usu­ally large en­ergy changes.

For the left of the two states, ${\vphantom' E}^{\rm e}_{\underline{\vec k},0}$ is just a bit larger than ${\vphantom' E}^{\rm e}_{{\vec k}.0}$, so the en­ergy change (10.15) due to the lat­tice po­ten­tial is large and neg­a­tive. All en­ergy de­creases will be rep­re­sented graph­i­cally by mov­ing the points to­wards the ori­gin, in or­der that the dis­tance from the ori­gin con­tin­ues to in­di­cate the en­ergy of the state. That means that the left state will move strongly to­wards the ori­gin. Con­sider now the other state just to the right; ${\vphantom' E}^{\rm e}_{\underline{\vec k},0}$ for that state is just a bit less than ${\vphantom' E}^{\rm e}_{{\vec k},0}$, so the en­ergy change of this state will be large and pos­i­tive; graph­i­cally, this point will move strongly away from the ori­gin. The re­sult is that the en­ergy lev­els are torn apart along the sur­face of the Wigner-Seitz cell.

Fig­ure 10.23: Ef­fect of a lat­tice po­ten­tial on the en­ergy. The en­ergy is rep­re­sented by the square dis­tance from the ori­gin, and is rel­a­tive to the en­ergy at the ori­gin.

That is il­lus­trated for an ar­bi­trar­ily cho­sen ex­am­ple lat­tice po­ten­tial in fig­ure 10.23. It is an­other rea­son why the Wigner-Seitz cell around the ori­gin, i.e. the first Bril­louin zone, is par­tic­u­larly im­por­tant. For dif­fer­ent lat­tices than the sim­ple cu­bic one con­sid­ered here, it is still the dis­tance from the ori­gin that is the de­cid­ing fac­tor, so in gen­eral, it is the Wigner-Seitz cell, rather than some par­al­lelepiped-shaped prim­i­tive cell along whose sur­faces the en­er­gies get torn apart.

Fig­ure 10.24: Bragg planes seen in wave num­ber space cross sec­tion.

But no­tice in fig­ure 10.23 that the en­ergy lev­els get torn apart along many more sur­faces than just the sur­face of the first Bril­louin zone. In gen­eral, it can be seen that tears oc­cur in wave num­ber space along all the per­pen­dic­u­lar bi­sec­tor planes, or Bragg planes, be­tween the points of the rec­i­p­ro­cal lat­tice and the ori­gin. Fig­ure 10.24 shows their in­ter­sec­tions with the cross sec­tion $k_z$ $\vphantom0\raisebox{1.5pt}{$=$}$ 0 as thin black lines. The $k_x$ and $k_y$ axes were left away to clar­ify that they do not hide any lines.

Re­call that the Bragg planes are also the bound­aries of the frag­ments that make up the var­i­ous Bril­louin zones. In fact the first Bril­louin zone is the cube or Wigner-Seitz cell around the ori­gin; (the square around the ori­gin in the cross sec­tion fig­ure 10.24). The sec­ond zone con­sists of six pyra­mid-shaped re­gions whose bases are the faces of the cube; (the four tri­an­gles shar­ing a side with the square in the cross sec­tion fig­ure 10.24). They can be pushed into the first Bril­louin zone us­ing the fun­da­men­tal trans­la­tion vec­tors to com­bine into a Wigner-Seitz cell shape.

Fig­ure 10.25: Oc­cu­pied states for the en­er­gies of fig­ure 10.23 if there are two va­lence elec­trons per lat­tice cell. Left: en­ergy. Right: wave num­bers.

Fig­ure 10.26: Smaller lat­tice po­ten­tial. From top to bot­tom shows one, two and three va­lence elec­trons per lat­tice cell. Left: en­ergy. Right: wave num­bers.

For a suf­fi­ciently strong lat­tice po­ten­tial like the one in fig­ure 10.23, the en­ergy lev­els in the first Bril­louin zone, the cen­ter patch, are every­where lower than in the re­main­ing ar­eas. Elec­trons will then oc­cupy these states first, and since there are $J\times{J}\times{J}$ spa­tial states in the zone, two va­lence elec­trons per phys­i­cal lat­tice cell will just fill it, fig­ure 10.25. That pro­duces an in­su­la­tor whose elec­trons are stuck in a filled va­lence band. The elec­trons must jump an fi­nite en­ergy gap to reach the out­ly­ing re­gions if they want to do any­thing non­triv­ial. Since no par­tic­u­lar re­quire­ments were put onto the lat­tice po­ten­tial, the form­ing of bands is self-ev­i­dently a very gen­eral process.

The wave num­ber space in the right half of fig­ure 10.25 also il­lus­trates that a lat­tice po­ten­tial can change the Flo­quet wave num­ber vec­tors that get oc­cu­pied. For the free-elec­tron gas, the oc­cu­pied states formed a spher­i­cal re­gion in terms of the wave num­ber vec­tors, as shown in the mid­dle of fig­ure 10.17, but here the oc­cu­pied states have be­come a cube, the Wigner-Seitz cell around the ori­gin. The Fermi sur­face seen in the ex­tended zone scheme is now no longer a spher­i­cal sur­face, but con­sists of the six faces of this cell.

But do not take this ex­am­ple too lit­er­ally: the small-​per­tur­ba­tion analy­sis is in­valid for the strong po­ten­tial re­quired for an in­su­la­tor, and the real pic­ture would look quite dif­fer­ent. In par­tic­u­lar, the roll-over of the states at the edge of the first Bril­louin zone in the en­ergy plot is a clear in­di­ca­tion that the ac­cu­racy is poor. The er­ror in the per­tur­ba­tion analy­sis is the largest for states im­me­di­ately next to the Bragg planes. The ex­am­ple is given just to il­lus­trate that the nearly-free elec­tron model can in­deed de­scribe band gaps if taken far enough.

The nearly-free elec­tron model is more rea­son­able for the smaller lat­tice forces ex­pe­ri­enced by va­lence elec­trons in met­als. For ex­am­ple, at re­duced strength, the same po­ten­tial as be­fore pro­duces fig­ure 10.26. Now the elec­trons have no trou­ble find­ing states of slightly higher en­ergy, as it should be for a metal. Note, in­ci­den­tally, that the Fermi sur­faces in the right-hand graphs seem to meet the Bragg planes much more nor­mally than the spher­i­cal free-elec­tron sur­face. That leads to smooth­ing out of the cor­ners of the sur­face seen in the pe­ri­odic zone scheme. For ex­am­ple, imag­ine the cen­ter zone of the one va­lence elec­tron wave num­ber space pe­ri­od­i­cally con­tin­ued.