| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
Subsections
A.38 Perturbation Theory
Most of the time in quantum mechanics, exact solution of the
Hamiltonian eigenvalue problem of interest is not possible. To deal
with that, approximations are made.
Perturbation theory can be used when the Hamiltonian 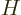 consists of
two parts
consists of
two parts  and
and 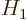 , where the problem for
, where the problem for  can be
solved and where
can be
solved and where 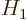 is small. The idea is then to adjust the found
solutions for the
is small. The idea is then to adjust the found
solutions for the unperturbed Hamiltonian
 so
that they become approximately correct for
so
that they become approximately correct for 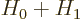 .
.
This addendum explains how perturbation theory works. It also gives a
few simple but important examples: the helium atom and the Zeeman and
Stark effects. Addendum,{A.39} will use the approach to
study relativistic effects on the hydrogen atom.
A.38.1 Basic perturbation theory
To use perturbation theory, the eigenfunctions and eigenvalues of the
unperturbed Hamiltonian  must be known. These eigenfunctions
will here be indicated as
must be known. These eigenfunctions
will here be indicated as  and the corresponding
eigenvalues by
and the corresponding
eigenvalues by 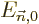 . Note the use of the generic
. Note the use of the generic  to indicate the quantum numbers of the eigenfunctions. If the basic
system is an hydrogen atom, as is often the case in textbook examples,
and spin is unimportant,
to indicate the quantum numbers of the eigenfunctions. If the basic
system is an hydrogen atom, as is often the case in textbook examples,
and spin is unimportant,  would likely stand for the set of
quantum numbers
would likely stand for the set of
quantum numbers  ,
,  , and
, and  . But for a
three-dimensional harmonic oscillator,
. But for a
three-dimensional harmonic oscillator,  might stand for the quantum
numbers
might stand for the quantum
numbers 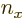 ,
,  , and
, and 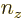 . In a three-dimensional
problem with one spinless particle, it takes three quantum numbers to
describe an energy eigenfunction. However, which three depends on the
problem and your approach to it. The additional subscript 0 in
. In a three-dimensional
problem with one spinless particle, it takes three quantum numbers to
describe an energy eigenfunction. However, which three depends on the
problem and your approach to it. The additional subscript 0 in
 and
and 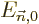 indicates that they ignore the
perturbation Hamiltonian
indicates that they ignore the
perturbation Hamiltonian 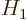 . They are called the unperturbed
wave functions and energies.
. They are called the unperturbed
wave functions and energies.
The key to perturbation theory are the “Hamiltonian perturbation coefficients” defined as
 |
(A.239) |
If you can evaluate these for every pair of energy eigenfunctions, you
should be OK. Note that evaluating inner products is just summation
or integration; it is generally a lot simpler than trying to solve the
eigenvalue problem 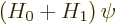

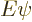 .
.
In the application of perturbation theory, the idea is to pick one
unperturbed eigenfunction  of
of  of interest and then
correct it to account for
of interest and then
correct it to account for 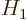 , and especially correct its
energy
, and especially correct its
energy 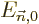 . Caution! If the energy
. Caution! If the energy 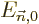 is
degenerate, i.e. there is more than one unperturbed eigenfunction
is
degenerate, i.e. there is more than one unperturbed eigenfunction
 of
of  with that energy, you must use a
with that energy, you must use a
good
eigenfunction to correct the energy. How to do
that will be discussed in subsection A.38.3.
For now just assume that the energy is not degenerate or that you
picked a good eigenfunction  . Then a first
correction to the energy
. Then a first
correction to the energy 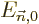 to account for the perturbation
to account for the perturbation
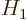 is very simple, {D.79}; just add the corresponding
Hamiltonian perturbation coefficient:
is very simple, {D.79}; just add the corresponding
Hamiltonian perturbation coefficient:
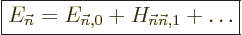 |
(A.240) |
This is a quite user-friendly result, because it only involves the
selected energy eigenfunction  . The other energy
eigenfunctions are not involved. In a numerical solution, you might
only have computed one state, say the ground state of
. The other energy
eigenfunctions are not involved. In a numerical solution, you might
only have computed one state, say the ground state of  .
Then you can use this result to correct the ground state energy for a
perturbation even if you do not have data about any other energy
states of
.
Then you can use this result to correct the ground state energy for a
perturbation even if you do not have data about any other energy
states of  .
.
Unfortunately, it does happen quite a lot that the above correction
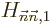 is zero because of some symmetry or the other.
Or it may simply not be accurate enough. In that case, to find the
energy change you have to use what is called “second order perturbation theory:”
is zero because of some symmetry or the other.
Or it may simply not be accurate enough. In that case, to find the
energy change you have to use what is called “second order perturbation theory:”
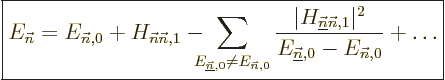 |
(A.241) |
Now all eigenfunctions of  will be needed, which makes second
order theory a lot nastier. Then again, even if the “first
order” correction
will be needed, which makes second
order theory a lot nastier. Then again, even if the “first
order” correction 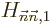 to the energy is
nonzero, the second order formula will likely give a much more
accurate result.
to the energy is
nonzero, the second order formula will likely give a much more
accurate result.
Sometimes you may also be interested in what happens to the energy
eigenfunctions, not just the energy eigenvalues. The corresponding
formula is
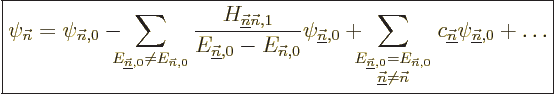 |
(A.242) |
That is the first order result. The second sum is zero if the problem
is not degenerate. Otherwise its coefficients
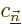 are determined by considerations found in
derivation {D.79}.
are determined by considerations found in
derivation {D.79}.
In some cases, instead of using second order theory as above, it may
be simpler to compute the first order wave function perturbation and
the second order energy change from
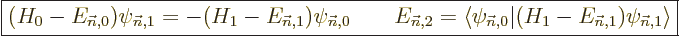 |
(A.243) |
Eigenfunction  must be good. The good news is that
this does not require all the unperturbed eigenfunctions. The bad
news is that it requires solution of a nontrivial equation involving
the unperturbed Hamiltonian instead of just integration. It may be
the best way to proceed for a perturbation of a numerical solution.
must be good. The good news is that
this does not require all the unperturbed eigenfunctions. The bad
news is that it requires solution of a nontrivial equation involving
the unperturbed Hamiltonian instead of just integration. It may be
the best way to proceed for a perturbation of a numerical solution.
One application of perturbation theory is the “Hellmann-Feynman theorem.” Here the perturbation Hamiltonian is
an infinitesimal change  in the unperturbed Hamiltonian
caused by an infinitesimal change in some parameter that it depends
on. If the parameter is called
in the unperturbed Hamiltonian
caused by an infinitesimal change in some parameter that it depends
on. If the parameter is called 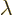 , perturbation theory
says that the first order energy change is
, perturbation theory
says that the first order energy change is
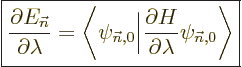 |
(A.244) |
when divided by the change in parameter  . If
you can figure out the inner product, you can figure out the change in
energy. But more important is the reverse: if you can find the
derivative of the energy with respect to the parameter, you have the
inner product. For example, the Hellmann-Feynman theorem is helpful
for finding the expectation value of 1
. If
you can figure out the inner product, you can figure out the change in
energy. But more important is the reverse: if you can find the
derivative of the energy with respect to the parameter, you have the
inner product. For example, the Hellmann-Feynman theorem is helpful
for finding the expectation value of 1
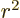 for the hydrogen atom, a
nasty problem, {D.83}. Of course, always make sure
the eigenfunction
for the hydrogen atom, a
nasty problem, {D.83}. Of course, always make sure
the eigenfunction  is a good one for the derivative of
the Hamiltonian.
is a good one for the derivative of
the Hamiltonian.
A.38.2 Ionization energy of helium
One prominent deficiency in the approximate analysis of the heavier
atoms in chapter 5.9 was the poor ionization energy that
it gave for helium. The purpose of this example is to derive a much
more reasonable value using perturbation theory.
Exactly speaking, the ionization energy is the difference between the
energy of the helium atom with both its electrons in the ground state
and the helium ion with its second electron removed. Now the energy
of the helium ion with electron 2 removed is easy; the Hamiltonian for
the remaining electron 1 is
where the first term represents the kinetic energy of the electron and
the second its attraction to the two-proton nucleus. The helium
nucleus normally also contains two neutrons, but they do not attract
the electron.
This Hamiltonian is exactly the same as the one for the hydrogen atom
in chapter 4.3, except that it has 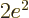 where the hydrogen
one, with just one proton in its nucleus, has
where the hydrogen
one, with just one proton in its nucleus, has 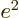 . So the
solution for the helium ion is simple: just take the hydrogen
solution, and everywhere where there is an
. So the
solution for the helium ion is simple: just take the hydrogen
solution, and everywhere where there is an 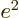 in that solution,
replace it by
in that solution,
replace it by 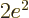 . In particular, the Bohr radius
. In particular, the Bohr radius  for
the helium ion is half the Bohr radius
for
the helium ion is half the Bohr radius 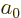 for hydrogen,
for hydrogen,
and so its energy and wave function become
where 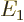

 13.6 eV is the energy of the hydrogen atom.
13.6 eV is the energy of the hydrogen atom.
It is interesting to see that the helium ion has four times the energy
of the hydrogen atom. The reasons for this much higher energy are
both that the nucleus is twice as strong, and that the electron is
twice as close to it: the Bohr radius is half the size. More
generally, in heavy atoms the electrons that are poorly shielded from
the nucleus, which means the inner electrons, have energies that scale
with the square of the nuclear strength. For such electrons,
relativistic effects are much more important than they are for the
electron in a hydrogen atom.
The neutral helium atom is not by far as easy to analyze as the ion.
Its Hamiltonian is, from (5.34):
The first two terms are the kinetic energy and nuclear attraction of
electron 1, and the next two the same for electron 2. The final term
is the electron to electron repulsion, the curse of quantum mechanics.
This final term is the reason that the ground state of helium cannot
be found analytically.
Note however that the repulsion term is qualitatively similar to the
nuclear attraction terms, except that there are four of these nuclear
attraction terms versus a single repulsion term. So maybe then, it
may work to treat the repulsion term as a small perturbation, call it
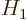 , to the Hamiltonian
, to the Hamiltonian  given by the first four terms?
Of course, if you ask mathematicians whether 25% is a small amount,
they are going to vehemently deny it; but then, so they would for any
amount if there is no limit process involved, so just don’t ask
them, OK?
given by the first four terms?
Of course, if you ask mathematicians whether 25% is a small amount,
they are going to vehemently deny it; but then, so they would for any
amount if there is no limit process involved, so just don’t ask
them, OK?
The solution of the eigenvalue problem 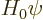

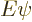 is simple:
since the electrons do not interact with this Hamiltonian, the ground
state wave function is the product of the ground state wave functions
for the individual electrons, and the energy is the sum of their
energies. And the wave functions and energies for the separate
electrons are given by the solution for the ion above, so
is simple:
since the electrons do not interact with this Hamiltonian, the ground
state wave function is the product of the ground state wave functions
for the individual electrons, and the energy is the sum of their
energies. And the wave functions and energies for the separate
electrons are given by the solution for the ion above, so
According to this result, the energy of the atom is 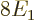 while the
ion had
while the
ion had 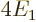 , so the ionization energy would be
, so the ionization energy would be
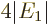 , or 54.4 eV. Since the experimental value is 24.6 eV,
this is no better than the 13.6 eV chapter 5.9 came up
with.
, or 54.4 eV. Since the experimental value is 24.6 eV,
this is no better than the 13.6 eV chapter 5.9 came up
with.
To get a better ionization energy, try perturbation theory. According
to first order perturbation theory, a better value for the energy of
the hydrogen atom should be
or substituting in from above,
The inner product of the final term can be written out as
This integral can be done analytically. Try it, if you are so
inclined; integrate 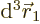 first, using spherical coordinates
with
first, using spherical coordinates
with 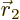 as their axis and doing the azimuthal and polar angles
first. Be careful,
as their axis and doing the azimuthal and polar angles
first. Be careful, 

 , not
, not
 , so you will have to integrate
, so you will have to integrate 
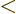
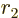 and
and


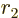 separately in the final integration over
separately in the final integration over
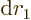 . Then integrate
. Then integrate 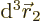 .
.
The result of the integration is
Therefore, the helium atom energy increases by 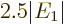 due to the
electron repulsion, and with it, the ionization energy decreases to
due to the
electron repulsion, and with it, the ionization energy decreases to
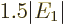 , or 20.4 eV. It is not 24.6 eV, but it is clearly
much more reasonable than 54 or 13.6 eV were.
, or 20.4 eV. It is not 24.6 eV, but it is clearly
much more reasonable than 54 or 13.6 eV were.
The second order perturbation result should give a much more accurate
result still. However, if you did the integral above, you may feel
little inclination to try the ones involving all possible products of
hydrogen energy eigenfunctions.
Instead, the result can be improved using a variational approach, like
the ones that were used earlier for the hydrogen molecule and
molecular ion, and this requires almost no additional work. The idea
is to accept the hint from perturbation theory that the wave function
of helium can be approximated as 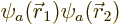 where
where
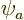 is the hydrogen ground state wave function using a modified
Bohr radius
is the hydrogen ground state wave function using a modified
Bohr radius  instead of
instead of 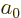 :
:
However, instead of accepting the perturbation theory result that  should be half the normal Bohr radius
should be half the normal Bohr radius 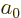 , let
, let  be
optimized to make the expectation energy for the ground state
be
optimized to make the expectation energy for the ground state
as small as possible. This will produce the most accurate ground
state energy possible for a ground state wave function of this form,
guaranteed no worse than assuming that 

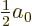 ,
and probably better.
,
and probably better.
No new integrals need to be done to evaluate the inner product above.
Instead, noting that for the hydrogen atom according to the virial
theorem of chapter 7.2 the expectation kinetic energy
equals 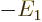

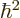

 and the potential energy
equals
and the potential energy
equals  , two of the needed integrals can be inferred from
the hydrogen solution: chapter 4.3,
, two of the needed integrals can be inferred from
the hydrogen solution: chapter 4.3,
and this subsection added
Using these results with the helium Hamiltonian, the expectation
energy of the helium atom can be written out to be
Setting the derivative with respect to  to zero locates the minimum
at
to zero locates the minimum
at 

 , rather than
, rather than 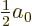 .
Then the corresponding expectation energy is
.
Then the corresponding expectation energy is



 , or
, or 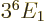

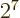 .
Putting in the numbers, the ionization energy is now found as 23.1 eV,
in quite good agreement with the experimental 24.6 eV.
.
Putting in the numbers, the ionization energy is now found as 23.1 eV,
in quite good agreement with the experimental 24.6 eV.
A.38.3 Degenerate perturbation theory
Energy eigenvalues are degenerate if there is more than one
independent eigenfunction with that energy. Now, if you try to use
perturbation theory to correct a degenerate eigenvalue of a
Hamiltonian  for a perturbation
for a perturbation 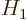 , there may be a
problem. Assume that there are
, there may be a
problem. Assume that there are 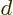
 1 independent eigenfunctions
with energy
1 independent eigenfunctions
with energy 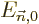 and that they are numbered as
and that they are numbered as
Then as far as  is concerned, any combination
is concerned, any combination
with arbitrary coefficients 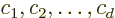 , (not all zero,
of course), is just as good an eigenfunction with energy
, (not all zero,
of course), is just as good an eigenfunction with energy 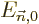 as any other.
as any other.
Unfortunately, the full Hamiltonian 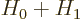 is not likely to agree
with
is not likely to agree
with  about that. As far as the full Hamiltonian is concerned,
normally only very specific combinations are acceptable, the
about that. As far as the full Hamiltonian is concerned,
normally only very specific combinations are acceptable, the
good
eigenfunctions. It is said that the perturbation
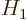
breaks the degeneracy
of the energy eigenvalue.
The single energy eigenvalue splits into several eigenvalues of
different energy. Only good combinations will show up these changed
energies; the bad ones will pick up uncertainty in energy that hides
the effect of the perturbation.
The various ways of ensuring good eigenfunctions are illustrated in
the following subsections for example perturbations of the energy
levels of the hydrogen atom. Recall that the unperturbed energy
eigenfunctions of the hydrogen atom electron, as derived in chapter
4.3, and also including spin, are given as 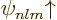 and
and 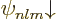 . They are highly degenerate: all the
eigenfunctions with the same value of
. They are highly degenerate: all the
eigenfunctions with the same value of  have the same energy
have the same energy
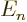 , regardless of what is the value of the azimuthal quantum
number 0
, regardless of what is the value of the azimuthal quantum
number 0 


 corresponding to the square orbital
angular momentum
corresponding to the square orbital
angular momentum 

 ; regardless of what
is the magnetic quantum number
; regardless of what
is the magnetic quantum number 

 corresponding to the
orbital angular momentum
corresponding to the
orbital angular momentum 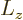

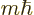 in the
in the  -direction;
and regardless of what is the spin quantum number
-direction;
and regardless of what is the spin quantum number 

 corresponding to the spin angular momentum
corresponding to the spin angular momentum 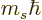 in
the
in
the  -direction. In particular, the ground state energy level
-direction. In particular, the ground state energy level 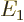 is two-fold degenerate, it is the same for both
is two-fold degenerate, it is the same for both 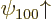 ,
i.e.
,
i.e. 

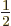 and
and 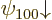 ,
, 

 . The next energy level
. The next energy level  is eight-fold
degenerate, it is the same for
is eight-fold
degenerate, it is the same for 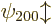 ,
,
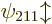 ,
, 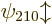 , and
, and
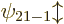 , and so on for higher values of
, and so on for higher values of  .
.
There are two important rules to identify the good eigenfunctions,
{D.79}:
-
1.
- Look for good quantum numbers. The quantum numbers that make
the energy eigenfunctions of the unperturbed Hamiltonian
 unique correspond to the eigenvalues of additional operators besides
the Hamiltonian. If the perturbation Hamiltonian
unique correspond to the eigenvalues of additional operators besides
the Hamiltonian. If the perturbation Hamiltonian 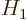 commutes
with one of these additional operators, the corresponding quantum
number is good. You do not need to combine eigenfunctions with
different values of that quantum number.
commutes
with one of these additional operators, the corresponding quantum
number is good. You do not need to combine eigenfunctions with
different values of that quantum number.
In particular, if the perturbation Hamiltonian commutes with all
additional operators that make the eigenfunctions of  unique,
stop worrying: every eigenfunction is good already.
unique,
stop worrying: every eigenfunction is good already.
For example, for the usual hydrogen energy eigenfunctions
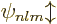 , the quantum numbers
, the quantum numbers  ,
,  ,
and
,
and  make the eigenfunctions at a given unperturbed energy
level
make the eigenfunctions at a given unperturbed energy
level  unique. They correspond to the operators
unique. They correspond to the operators 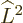 ,
,
 , and
, and  . If the perturbation Hamiltonian
. If the perturbation Hamiltonian
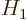 commutes with any one of these operators, the corresponding
quantum number is good. If the perturbation commutes with all
three, all eigenfunctions are good already.
commutes with any one of these operators, the corresponding
quantum number is good. If the perturbation commutes with all
three, all eigenfunctions are good already.
-
2.
- Even if some quantum numbers are bad because the perturbation
does not commute with that operator, eigenfunctions are still good
if there are no other eigenfunctions with the same unperturbed
energy and the same good quantum numbers.
Otherwise linear algebra is required. For each set of energy
eigenfunctions
with the same unperturbed energy and the same good quantum numbers,
but different bad ones, form the matrix of Hamiltonian perturbation
coefficients
The eigenvalues of this matrix are the first order energy
corrections. Also, the coefficients 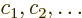 of each good
eigenfunction
of each good
eigenfunction
must be an eigenvector of the matrix.
Unfortunately, if the eigenvalues of this matrix are not all
different, the eigenvectors are not unique, so you remain unsure
about what are the good eigenfunctions. In that case, if the second
order energy corrections are needed, the detailed analysis of
derivation {D.79} will need to be followed.
If you are not familiar with linear algebra at all, in all cases
mentioned here the matrices are just two by two, and you can find
that solution spelled out in the notations under
eigenvector.
The following, related, practical observation can also be made:
Hamiltonian perturbation coefficients can only be nonzero if all the
good quantum numbers are the same.
A.38.4 The Zeeman effect
If you put an hydrogen atom in an external magnetic field
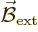 , the energy levels of the electron change.
That is called the
, the energy levels of the electron change.
That is called the Zeeman effect.
If for simplicity a coordinate system is used with its  -axis
aligned with the magnetic field, then according to chapter
13.4, the Hamiltonian of the hydrogen atom acquires an
additional term
-axis
aligned with the magnetic field, then according to chapter
13.4, the Hamiltonian of the hydrogen atom acquires an
additional term
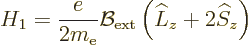 |
(A.245) |
beyond the basic hydrogen atom Hamiltonian  of chapter
4.3.1. Qualitatively, it expresses that a spinning charged
particle is equivalent to a tiny electromagnet, and a magnet wants to
align itself with a magnetic field, just like a compass needle aligns
itself with the magnetic field of earth.
of chapter
4.3.1. Qualitatively, it expresses that a spinning charged
particle is equivalent to a tiny electromagnet, and a magnet wants to
align itself with a magnetic field, just like a compass needle aligns
itself with the magnetic field of earth.
For this perturbation, the  energy eigenfunctions are
already good ones, because
energy eigenfunctions are
already good ones, because 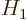 commutes with all of
commutes with all of 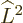 ,
,
 and
and  . So, according to perturbation theory, the
energy eigenvalues of an hydrogen atom in a magnetic field are
approximately
. So, according to perturbation theory, the
energy eigenvalues of an hydrogen atom in a magnetic field are
approximately
Actually, this is not approximate at all; it is the exact eigenvalue
of 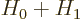 corresponding to the exact eigenfunction
corresponding to the exact eigenfunction
 .
.
The Zeeman effect can be seen in an experimental spectrum. Consider
first the ground state. If there is no electromagnetic field, the two
ground states 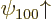 and
and 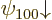 would have exactly
the same energy. Therefore, in an experimental spectrum, they would
show up as a single line. But with the magnetic field, the two energy
levels are different,
would have exactly
the same energy. Therefore, in an experimental spectrum, they would
show up as a single line. But with the magnetic field, the two energy
levels are different,
so the single line splits into two! Do note that the energy change
due to even an extremely strong magnetic field of 100 Tesla is only
0.006 eV or so, chapter 13.4, so it is not like the
spectrum would become unrecognizable. The single spectral line of the
eight 
L
shell states will similarly
split in five closely spaced but separate lines, corresponding to the
five possible values  2,
2,  1, 0, 1 and 2 for the factor
1, 0, 1 and 2 for the factor
 above.
above.
Some disclaimers should be given here. First of all, the 2 in
 is only equal to 2 up to about 0.1% accuracy. More
importantly, even in the absence of a magnetic field, the energy
levels at a given value of
is only equal to 2 up to about 0.1% accuracy. More
importantly, even in the absence of a magnetic field, the energy
levels at a given value of  do not really form a single line in the
spectrum if you look closely enough. There are small errors in the
solution of chapter 4.3 due to relativistic effects, and so
the theoretical lines are already split. That is discussed in
addendum {A.39}. The description given above is a good one
for the
do not really form a single line in the
spectrum if you look closely enough. There are small errors in the
solution of chapter 4.3 due to relativistic effects, and so
the theoretical lines are already split. That is discussed in
addendum {A.39}. The description given above is a good one
for the strong
Zeeman effect, in which the magnetic
field is strong enough to swamp the relativistic errors.
A.38.5 The Stark effect
If an hydrogen atom is placed in an external electric field
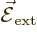 instead of the magnetic one of the previous
subsection, its energy levels will change too. That is called the
instead of the magnetic one of the previous
subsection, its energy levels will change too. That is called the
Stark effect.
Of course a Zeeman, Dutch for sea-man,
would be most interested in magnetic fields. A Stark, maybe in a
spark? (Apologies.)
If the  -axis is taken in the direction of the electric field, the
contribution of the electric field to the Hamiltonian is given by:
-axis is taken in the direction of the electric field, the
contribution of the electric field to the Hamiltonian is given by:
 |
(A.246) |
It is much like the potential energy  of gravity, with the
electron charge
of gravity, with the
electron charge 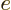 taking the place of the mass
taking the place of the mass  ,
,
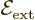 that of the gravity strength
that of the gravity strength  , and
, and  that
of the height
that
of the height 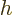 .
.
Since the typical magnitude of  is of the order of a Bohr radius
is of the order of a Bohr radius
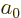 , you would expect that the energy levels will change due
to the electric field by an amount of rough size
, you would expect that the energy levels will change due
to the electric field by an amount of rough size
 . A strong laboratory electric field might
have
. A strong laboratory electric field might
have  of the order of 0.000 5 eV,
[25, p. 339]. That is really small compared to the
typical electron energy levels.
of the order of 0.000 5 eV,
[25, p. 339]. That is really small compared to the
typical electron energy levels.
And additionally, it turns out that for many eigenfunctions, including
the ground state, the first order correction to the energy is zero.
To get the energy change in that case, you need to compute the second
order term, which is a pain. And that term will be much smaller still
than even  for reasonable field strengths.
for reasonable field strengths.
Now first suppose that you ignore the warnings on good eigenfunctions,
and just compute the energy changes using the inner product
 . You will then
find that this inner product is zero for whatever energy eigenfunction
you take:
. You will then
find that this inner product is zero for whatever energy eigenfunction
you take:
The reason is that negative  values integrate away against positive
ones. (The inner products are integrals of
values integrate away against positive
ones. (The inner products are integrals of  times
times
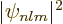 , and
, and 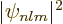 is the same at opposite
sides of the nucleus while
is the same at opposite
sides of the nucleus while  changes sign, so the contributions of
opposite sides to the inner product pairwise cancel.)
changes sign, so the contributions of
opposite sides to the inner product pairwise cancel.)
So, since all first order energy changes that you compute are zero,
you would naturally conclude that to first order approximation none of
the energy levels of a hydrogen atom changes due to the electric
field. But that conclusion is wrong for anything but the ground state
energy. And the reason it is wrong is because the good eigenfunctions
have not been used.
Consider the operators 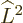 ,
,  , and
, and 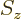 that make
the energy eigenfunctions
that make
the energy eigenfunctions 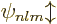 unique. If
unique. If 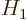

 commuted with them all, the
commuted with them all, the 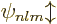 would
be good eigenfunctions. Unfortunately, while
would
be good eigenfunctions. Unfortunately, while  commutes with
commutes with  and
and 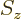 , it does not commute with
, it does not commute with 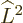 , see chapter
4.5.4. The quantum number
, see chapter
4.5.4. The quantum number  is bad.
is bad.
Still, the two states 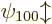 with the ground state energy
are good states, because there are no states with the same energy and
a different value of the bad quantum number
with the ground state energy
are good states, because there are no states with the same energy and
a different value of the bad quantum number  . Really, spin
has nothing to do with the Stark problem. If you want, you can find
the purely spatial energy eigenfunctions first, then for every spatial
eigenfunction, there will be one like that with spin up and one with
spin down. In any case, since the two eigenfunctions
. Really, spin
has nothing to do with the Stark problem. If you want, you can find
the purely spatial energy eigenfunctions first, then for every spatial
eigenfunction, there will be one like that with spin up and one with
spin down. In any case, since the two eigenfunctions 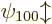 are both good, the ground state energy does indeed not change to first
order.
are both good, the ground state energy does indeed not change to first
order.
But now consider the eight-fold degenerate 
 2 energy level.
Each of the four eigenfunctions
2 energy level.
Each of the four eigenfunctions 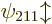 and
and
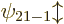 is a good one because for each of them, there is
no other
is a good one because for each of them, there is
no other 
 2 eigenfunction with a different value of the bad
quantum number
2 eigenfunction with a different value of the bad
quantum number  . The energies corresponding to these good
eigenfunctions too do indeed not change to first order.
. The energies corresponding to these good
eigenfunctions too do indeed not change to first order.
However, the remaining two 
 2 spin-up states
2 spin-up states  and
and 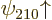 have different values for the bad quantum number
have different values for the bad quantum number
 , and they have the same values
, and they have the same values 
 0 and
0 and 

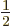 for the good quantum numbers of orbital and spin
for the good quantum numbers of orbital and spin
 -momentum. These eigenfunctions are bad and will have to be
combined to produce good ones. And similarly the remaining two
spin-down states
-momentum. These eigenfunctions are bad and will have to be
combined to produce good ones. And similarly the remaining two
spin-down states  and
and 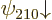 are bad and will
have to be combined.
are bad and will
have to be combined.
It suffices to just analyze the spin up states, because the spin down
ones go exactly the same way. The coefficients 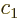 and
and  of the
good combinations
of the
good combinations  must be
eigenvectors of the matrix
must be
eigenvectors of the matrix
The diagonal
elements of this matrix (top left corner
and bottom right corner) are zero because of cancellation of negative
and positive  values as discussed above. And the top right and
bottom left elements are complex conjugates, (2.16), so only
one of them needs to be actually computed. And the spin part of the
inner product produces one and can therefore be ignored. What is left
is a matter of finding the two spatial eigenfunctions involved
according to (4.36), looking up the spherical harmonics in
table 4.2 and the radial functions in table 4.4, and
integrating it all against
values as discussed above. And the top right and
bottom left elements are complex conjugates, (2.16), so only
one of them needs to be actually computed. And the spin part of the
inner product produces one and can therefore be ignored. What is left
is a matter of finding the two spatial eigenfunctions involved
according to (4.36), looking up the spherical harmonics in
table 4.2 and the radial functions in table 4.4, and
integrating it all against  . The resulting
matrix is
. The resulting
matrix is
The eigenvectors of this matrix are simple enough to guess; they have
either equal or opposite coefficients 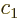 and
and  :
:
If you want to check these expressions, note that the product of a
matrix times a vector is found by taking dot products between the rows
of the matrix and the vector. It follows that the good combination
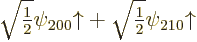 has a first
order energy change
has a first
order energy change 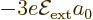 , and the good
combination
, and the good
combination 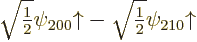 has
has 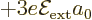 . The same applies for the spin down
states. It follows that to first order the
. The same applies for the spin down
states. It follows that to first order the 
 2 level splits
into three, with energies
2 level splits
into three, with energies 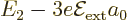 ,
,
 , and
, and 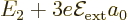 , where the value
, where the value
 applies to the eigenfunctions
applies to the eigenfunctions 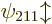 and
and
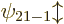 that were already good. The conclusion, based on
the wrong eigenfunctions, that the energy levels do not change was all
wrong.
that were already good. The conclusion, based on
the wrong eigenfunctions, that the energy levels do not change was all
wrong.
Remarkably, the good combinations of 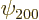 and
and 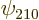 are
the
are
the sp
hybrids of carbon fame, as described in chapter
5.11.4. Note from figure 5.13 in that section
that these hybrids do not have the same magnitude at opposite
sides of the nucleus. They have an intrinsic “electric dipole
moment,” with the charge shifted towards one side of the atom,
and the electron then wants to align this dipole moment with the
ambient electric field. That is much like in Zeeman splitting, where
electron wants to align its orbital and spin magnetic dipole moments
with the ambient magnetic field.
The crucial thing to take away from all this is: always, always, check
whether the eigenfunction is good before applying perturbation theory.
It is obviously somewhat disappointing that perturbation theory did
not give any information about the energy change of the ground state
beyond the fact that it is second order, i.e. very small compared to
 . You would like to know approximately what
it is, not just that it is very small. Of course, now that it is
established that
. You would like to know approximately what
it is, not just that it is very small. Of course, now that it is
established that 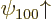 is a good state with
is a good state with 
 0 and
0 and


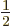 , you could think about evaluating the
second order energy change (A.241), by integrating
, you could think about evaluating the
second order energy change (A.241), by integrating
 for all
values of
for all
values of  and
and  . But after refreshing your memory about
the analytical expression (D.8) for the
. But after refreshing your memory about
the analytical expression (D.8) for the 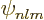 ,
you might think again.
,
you might think again.
It is however possible to find the perturbation in the wave function
from the alternate approach (A.243), {D.80}.
In that way the second order ground state energy is found to be
Note that the atom likes an electric field: it lowers its ground state
energy. Also note that the energy change is indeed second order; it
is proportional to the square of the electric field strength. You can
think of the attraction of the atom to the electric field as a
two-stage process: first the electric field polarizes the atom by
distorting its initially symmetric charge distribution. Then it
interacts with this polarized atom in much the same way that it
interacts with the sp hybrids. But since the polarization is now only
proportional to the field strength, the net energy drop is
proportional to the square of the field strength.
Finally, note that the typical value of 0.000 5 eV or so for
 quoted earlier is very small compared to the
about 100 eV for
quoted earlier is very small compared to the
about 100 eV for 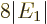 , making the fraction in the expression
above very small. So, indeed the second order change in the ground
state energy
, making the fraction in the expression
above very small. So, indeed the second order change in the ground
state energy 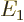 is much smaller than the first order energy changes
is much smaller than the first order energy changes
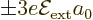 in the
in the  energy level.
energy level.
A weird prediction of quantum mechanics is that the electron will
eventually escape from the atom, leaving it ionized. The reason is
that the potential is linear in  , so if the electron goes out
far enough in the
, so if the electron goes out
far enough in the  -direction, it will eventually encounter
potential energies that are lower than the one it has in the atom. Of
course, to get at such large values of
-direction, it will eventually encounter
potential energies that are lower than the one it has in the atom. Of
course, to get at such large values of  , the electron must
pass positions where the required energy far exceeds the
, the electron must
pass positions where the required energy far exceeds the  13.6 eV it
has available, and that is impossible for a classical particle.
However, in quantum mechanics the position of the electron is
uncertain, and the electron does have some miniscule chance of
13.6 eV it
has available, and that is impossible for a classical particle.
However, in quantum mechanics the position of the electron is
uncertain, and the electron does have some miniscule chance of
tunneling out
of the atom through the energy barrier,
chapter 7.12.2. Realistically, though, for even strong
experimental fields like the one mentioned above, the “life
time” of the electron in the atom before it has a decent chance
of being found outside it far exceeds the age of the universe.
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]() .
.![]()
![]()
![]() .
.![]()
![]()
![]() ,
,![]() ,
,![]() .
.![]()
![]() ,
,![]() ,
,![]() .
.![]()
![]()
![]() .
.![]()
![]()
![]() ,
,![]() .
.![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]() ,
,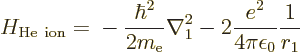
![]()
![]() .
.![]()
![]() .
.![]()
![]()


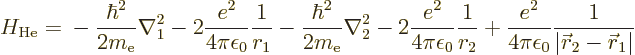
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]() ,
,![]() ,
,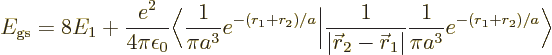
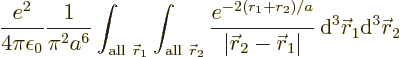
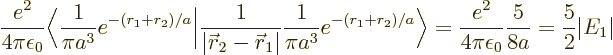
![]()
![]()
![]()
![]() :
: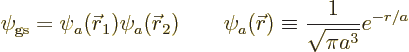
![]()
![]()
![]()
![]()
![]()
![]() ,
,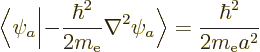
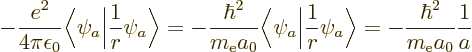
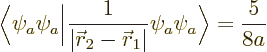
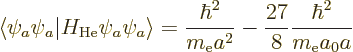
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]() ;
;![]()
![]()
![]()
![]()
![]()
![]()
![]() -
-![]()
![]()
![]()
![]()
![]() -
-![]()
![]() ,
,![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() .
.![]()
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.![]()
![]() ,
,![]() ,
,![]() ,
,![]()
![]()
![]() ,
,![]() ,
,![]() .
.![]()
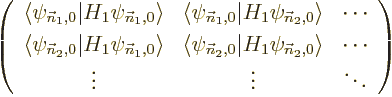
![]() ,
,![]() -
-![]()
![]()
![]() ,
,![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]() -
-![]()
![]() ,
,![]() .
.![]()
![]()
![]() .
.![]() ,
,![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]() ,
,![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]() -
-![]()
![]()
![]()
![]()
![]()
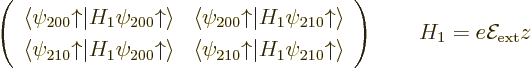

![]()
![]() :
: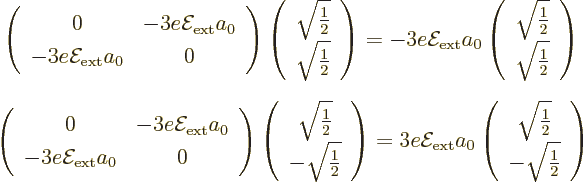
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() .
.![]() ,
,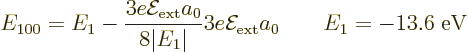
![]()
![]() ,
,![]()
![]()
![]()
![]() ,
,![]() -
-![]() ,
,![]() 1
1