|
|
|
|
|
Next: 11. Basic and Quantum Thermodynamics |
|
This section mentions a couple of additional very basic issues in the quantum mechanics of solids.
Magnetism in all its myriad forms and complexity is far beyond the scope of this book. But there is one very important fundamental quantum mechanics issue associated with ferromagnetism that has not yet been introduced.
Ferromagnetism is the plain variety of magnetism, like in refrigerator magnets. Ferromagnetic solids like iron are of great engineering interest. They can significantly increase a magnetic field and can stay permanently magnetized even in the absence of a field. The fundamental quantum mechanics issue has to do with why they produce magnetic fields in the first place.
The source of the ferromagnetic field is the electrons. Electrons
have spin, and just like a classical charged particle that is spinning
around in a circle produces a magnetic field, so do electrons act as
little magnets. A free iron atom has 26 electrons, each with spin
![]() .
.
However, iron has a final six electrons in 3d states, and the 3d states can accommodate ten electrons, five for each spin direction. So only two out of the six electrons need to enter the same spatial state as a zero spin singlet. The other four electrons can each go into their private spatial state. And the electrons do want to do so, since by going into different spatial states, they can stay farther away from each other, minimizing their mutual Coulomb repulsion energy.
According to the simplistic model of noninteracting electrons that was used to describe atoms in chapter 5.9, these last four electrons can then have equal or opposite spin, whatever they like. But that is wrong. The four electrons interact through their Coulomb repulsion, and it turns out that they achieve the smallest energy when their spatial wave function is antisymmetric under particle exchange.
(This is just the opposite of the conclusion for the hydrogen molecule, where the symmetric spatial wave function had the lowest energy. The difference is that for the hydrogen molecule, the dominant effect is the reduction of the kinetic energy that the symmetric state achieves, while for the single-atom states, the dominant effect is the reduction in electron to electron Coulomb repulsion that the antisymmetric wave function achieves. In the antisymmetric spatial wave function, the electrons stay further apart on average.)
If the spatial wave function of the four electrons takes care of the antisymmetrization requirement, then their spin state cannot change under particle exchange; they all must have the same spin. This is known as “Hund’s first rule:” electron interaction makes the net spin as big as the exclusion principle allows. The four unpaired 3d electrons in iron minimize their Coulomb energy at the price of having to align all four of their spins. Which means their spin magnetic moments add up rather than cancel each other. {A.34}.
Hund’s second rule says that the electrons will next maximize their orbital angular momentum as much as is still possible. And according to Hund’s third rule, this orbital angular momentum will add to the spin angular momentum since the ten 3d states are more than half full. It turns out that iron’s 3d electrons have the same amount of orbital angular momentum as spin, however, orbital angular momentum is only about half as effective at creating a magnetic dipole.
In addition, the magnetic properties of orbital angular momentum are readily messed up when atoms are brought together in a solid, and more so for transition metals like iron than for the lanthanoid series, whose unfilled 4f states are buried much deeper inside the atoms. In most of the common ferromagnets, the orbital contribution is negligible small, though in some rare earths there is an appreciable orbital contribution.
Guessing just the right amounts of net spin angular momentum, net
orbital angular momentum, and net combined angular momentum for an
atom can be tricky. So, in an effort make quantum mechanics as
readily accessible as possible, physicists provide the data in an
intuitive hieroglyph. For example
On to the solid. The atoms act as little magnets because of their four aligned electron spins and net orbital angular momentum, but why would different atoms want to align their magnetic poles in the same direction in a solid? If they don’t, there is not going to be any macroscopically significant magnetic field. The logical reason for the electron spins of different atoms to align would seem to be that it minimizes the magnetic energy. However, if the numbers are examined, any such aligning force is far too small to survive random heat motion at normal temperatures.
The primary reason is without doubt again the same weird quantum mechanics as for the single atom. Nature does not care about magnetic alignment or not; it is squirming to minimize its Coulomb energy under the massive constraints of the antisymmetrization requirement. By aligning electron spins globally, it achieves that electrons can stay farther apart spatially. {N.22}.
It is a fairly small effect; among the pure elements, it really only works under normal operating temperatures for cobalt and its immediate neighbors in the periodic table, iron and nickel. And alignment is normally not achieved throughout a bulk solid, but only in microscopic zones, with different zones having different alignment. But any electrical engineer will tell you it is a very important effect anyway. For one since the zones can be manipulated with a magnetic field.
And it clarifies that nature does not necessarily select singlet states of opposite spin to minimize the energy, despite what the hydrogen molecule and helium atom might suggest. Much of the time, aligned spins are preferred.
You may wonder how so much is known about the crystal structure of solids in view of the fact that the atoms are much too small to be seen with visible light. In addition, because of the fact that the energy levels get smeared out into bands, like in figure 10.11, solids do not have those tell-tale line spectra that are so useful for analyzing atoms and molecules.
To be precise, while the energy levels of the outer electrons of the atoms get smeared out, those of the inner electrons do not do so significantly, and these do produce line spectra. But since the energy levels of the inner electrons are very high, transitions involving inner electrons do not produce visible light, but X-rays.
There is a very powerful other technique for studying the crystal structure of atoms, however, and it also involves X-rays. In this technique, called X-ray diffraction, an X-ray is trained on a crystal from various angles, and the way the crystal scatters the X-ray is determined.
There is no quantum mechanics needed to describe how this works, but a brief description may be of value anyway. If you want to work in nano-technology, you will inevitably run up against experimental work, and X-ray diffraction is a key technique. Having some idea of how it works and what it can do can be useful.
First a very basic understanding is needed of what is an X-ray. An X-ray is a propagating wave of electromagnetic radiation just like a beam of visible light. The only difference between them is that an X-ray is much more energetic. Whether it is light or an X-ray, an electromagnetic wave is physically a combination of electric and magnetic fields that propagate in a given direction with the speed of light.
Figure 10.27 gives a sketch of how the strength of the electric field varies along the propagation direction of a simple monochromatic wave; the magnetic field is similar, but 90 degrees out of phase. Above that, a sketch is given how such rays will be visualized in this subsection: the positive maxima will be indicated by encircled plus signs, and the negative minima by encircled minus signs. Both these maxima and minima propagate along the line with the speed of light; the picture is just a snapshot at an arbitrary time.
The distance between two successive maxima is called the wave length
![]() .
.
The wave number ![]()
![]() :
:![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
Next consider a plane of atoms in a crystal, and imagine that it forms a perfectly flat mirror, as in figure 10.28. No, there are no physical examples of flat atoms known to science. But just imagine there would be, OK? Now shine an X-ray from the left onto this crystal layer and examine the diffracted wave that comes back from it. Assume Huygens’ principle that the scattered rays come off in all directions, and that the scattering is elastic, meaning that the energy, hence wave length, stays the same.
Under those conditions, a detector A, placed at a position to catch
the rays scattered to the same angle as the angle ![]()
![]()
Detector B, at a position where the angle of reflection is unequal to the angle of incidence, receives similar rays, but both positive and negative values of the electric field arrive at B at the same time, killing each other off. So detector B will not see an observable signal. That is the law of reflection: there is only a detectable diffracted wave at a position where the angle of reflection equals the angle of incidence. (Those angles are usually measured from the normal to the surface instead of from the surface itself, but not in Bragg diffraction.)
For visible light, this is actually a quite reasonable analysis of a mirror, since an atom-size surface roughness is negligible compared to the wave length of visible light. For X-rays, it is not so hot, partly because a layer of atoms is not flat on the scale of the wave length of the X-ray. But worse, a single layer of atoms does not reflect an X-ray by any appreciable amount. That is the entire point of medical X-rays; they can penetrate millions of layers of atoms to show what is below. A single layer is nothing to them.
For X-rays to be diffracted in an appreciable amount, it must be done
by many parallel layers of atoms, not just one, as in figure
10.29. The layers must furthermore have a very specific
spacing ![]()
The spacing between planes needed to get a decent combined signal
strength at the detector is known to satisfy the Bragg law:
The above story is, of course, not very satisfactory. For one, layers of atoms are not flat planes on the scale of the required X-ray wave lengths. And how come that in one direction the atoms have continuous positions and in another discrete? Furthermore, it is not obvious what to make of the results. Observing a refracted X-ray at some angular location may suggest that there is some reflecting plane in the crystal at an angle deducible from the law of reflection, but many different planes of atoms exist in a crystal. If a large number of measurements are done, typically by surrounding the specimen by detectors and rotating it while shining an X-ray on it, how is the crystal structure to be deduced from that overwhelming amount of information?
Clearly, a mathematical analysis is needed, and actually it is not
very complicated. First a mathematical expression is needed for the
signal along the ray; it can be taken to be a complex exponential
So, how much is the phase factor ![]() ?
?![]() .
.![]()
![]() .
.![]() :
:
The net result is then that the phase factor with which the ray from P
arrives at the detector compared to the ray from O is
First of all, for the law of reflection of figure 10.28,
the positions of the scattering points P vary continuously through the
horizontal plane. That means that the phase factor of the rays
received at the detector will normally also vary continuously from
positive to negative back to positive etcetera, leading to large-scale
cancelation of the net signal. The one exception is when
![]()
![]()
![]()
![]()
Next for Bragg’s law of figure 10.29, the issue is the
phase difference between successive crystal planes. So the vector
![]()
![]()
![]()
![]() .
.![]() ,
,![]()
![]() .
.![]() .
.![]()
![]()
![]() .
.
Now how about diffraction from a real crystal? Well, assume
that every location in the crystal elastically scatters the incoming
wave by a small amount that is proportional to the electron density
![]()
![]()
![]()
![]()
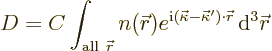
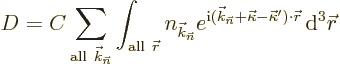
| (10.17) |
So the changes in the x-ray wave number vector ![]()
![]()
![]()
One interesting additional issue has to do with what incoming wave
vectors ![]()
![]()
![]()
![]()
| (10.18) |
Historically, Bragg diffraction was important to show that particles are indeed
associated with wave functions, as de Broglie had surmised. When
Davisson and Germer bombarded a crystal with a beam of single-momentum
electrons, they observed Bragg diffraction just like for
electromagnetic waves. Assuming for simplicity that the momentum of
the electrons is in the ![]() -
-![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]() -
-![]()
![]()
![]()
![]()