9.2 The Born-Op­pen­heimer Ap­prox­i­ma­tion

Ex­act so­lu­tions in quan­tum me­chan­ics are hard to come by. In al­most all cases, ap­prox­i­ma­tion is needed. The Born-Op­pen­heimer ap­prox­i­ma­tion in par­tic­u­lar is a key part of real-life quan­tum analy­sis of atoms and mol­e­cules and the like. The ba­sic idea is that the un­cer­tainty in the nu­clear po­si­tions is too small to worry about when you are try­ing to find the wave func­tion for the elec­trons. That was al­ready as­sumed in the ear­lier ap­prox­i­mate so­lu­tions for the hy­dro­gen mol­e­cule and mol­e­c­u­lar ion. This sec­tion dis­cusses the ap­prox­i­ma­tion, and how it can be used, in more depth.

9.2.1 The Hamil­ton­ian

The gen­eral prob­lem to be dis­cussed in this sec­tion is that of a num­ber of elec­trons around a num­ber of nu­clei. You first need to know what is the true prob­lem to be solved, and for that you need the Hamil­ton­ian.

This dis­cus­sion will be re­stricted to the strictly non­rel­a­tivis­tic case. Cor­rec­tions for rel­a­tivis­tic ef­fects on en­ergy, in­clud­ing those in­volv­ing spin, can in prin­ci­ple be added later, though that is well be­yond the scope of this book. The phys­i­cal prob­lem to be ad­dressed is that there are a fi­nite num­ber $I$ of elec­trons around a fi­nite num­ber $J$ of nu­clei in oth­er­wise empty space. That de­scribes ba­sic sys­tems of atoms and mol­e­cules, but mod­i­fi­ca­tions would have to be made for am­bi­ent elec­tric and mag­netic fields and elec­tro­mag­netic waves, or for the in­fi­nite sys­tems of elec­trons and nu­clei used to de­scribe solids.

The elec­trons will be num­bered us­ing an in­dex $i$, and when­ever there is a sec­ond elec­tron in­volved, its in­dex will be called ${\underline i}$. Sim­i­larly, the nu­clei will be num­bered with an in­dex $j$, or ${\underline j}$ where needed. The nu­clear charge of nu­cleus num­ber $j$, i.e. the num­ber of pro­tons in that nu­cleus, will be in­di­cated by $Z_j$, and the mass of the nu­cleus by $m^{\rm n}_j$. Roughly speak­ing, the mass $m^{\rm n}_j$ will be the sum of the masses of the pro­tons and neu­trons in the nu­cleus; how­ever, in­ter­nal nu­clear en­er­gies are big enough that there are no­tice­able rel­a­tivis­tic de­vi­a­tions in to­tal nu­clear rest mass from what you would think. All the elec­trons have the same mass $m_{\rm e}$ since rel­a­tivis­tic mass changes due to mo­tion are ig­nored.

Un­der the stated as­sump­tions, the Hamil­ton­ian of the sys­tem con­sists of a num­ber of con­tri­bu­tions that will be looked at one by one. First there is the ki­netic en­ergy of the elec­trons, the sum of the ki­netic en­ergy op­er­a­tors of the in­di­vid­ual elec­trons:

$${\widehat T}^{\rm E} = - \sum_{i=1}^I \frac{\hbar^2}{2m_{\... ...{2i}}^2} + \frac{\partial^2}{\partial {r_{3i}}^2} \right). %$$ (9.4)

where ${\skew0\vec r}_i$ $\vphantom0\raisebox{1.5pt}{$=$}$ $(r_{1i},r_{2i},r_{3i})$ is the po­si­tion of elec­tron num­ber $i$. Note the use of $(r_1,r_2,r_3)$ as the no­ta­tion for the com­po­nents of po­si­tion, rather than $(x,y,z)$. For more elab­o­rate math­e­mat­ics, the in­dex no­ta­tion $(r_1,r_2,r_3)$ is of­ten more con­ve­nient, since you can in­di­cate any generic com­po­nent by the sin­gle ex­pres­sion $r_\alpha$, (with the un­der­stand­ing that $\alpha$ $\vphantom0\raisebox{1.5pt}{$=$}$ 1, 2, or 3,) in­stead of writ­ing them out all three sep­a­rately.

Sim­i­larly, there is the ki­netic en­ergy of the nu­clei,

$${\widehat T}^{\rm N} = - \sum_{j=1}^J \frac{\hbar^2}{2m^{\... ... + \frac{\partial^2}{\partial {r^{\rm n}_{3j}}^2} \right). %$$ (9.5)

where ${\skew0\vec r}^{\,\rm {n}}_j$ $\vphantom0\raisebox{1.5pt}{$=$}$ $(r^{\rm n}_{1j},r^{\rm n}_{2j},r^{\rm n}_{3j})$ is the po­si­tion of nu­cleus num­ber $j$.

Next there is the po­ten­tial en­ergy due to the at­trac­tion of the $I$ elec­trons by the $J$ nu­clei. That po­ten­tial en­ergy is, sum­ming over all elec­trons and over all nu­clei:

$$V^{\rm NE}= - \sum_{i=1}^I \sum_{j=1}^J \frac{Z_j e^2}{4\pi\epsilon_0} \frac{1}{r_{ij}} %$$ (9.6)

where $r_{ij}\equiv\vert{\skew0\vec r}_i-{\skew0\vec r}^{\,\rm {n}}_j\vert$ is the dis­tance be­tween elec­tron num­ber $i$ and nu­cleus num­ber $j$, and $\epsilon_0$ $\vphantom0\raisebox{1.5pt}{$=$}$ 8.85 10$\POW9,{-12}$ C$\POW9,{2}$/J m is the per­mit­tiv­ity of space.

Next there is the po­ten­tial en­ergy due to the elec­tron-elec­tron re­pul­sions:

$$V^{\rm EE}= {\textstyle\frac{1}{2}} \sum_{i=1}^I \sum_{\t... ...^I \frac{e^2}{4\pi\epsilon_0} \frac{1}{r_{i{\underline i}}} %$$ (9.7)

where $r_{i{\underline i}}\equiv\vert{\skew0\vec r}_i-{\skew0\vec r}_{\underline i}\vert$ is the dis­tance be­tween elec­tron num­ber $i$ and elec­tron num­ber ${\underline i}$. Half of this re­pul­sion en­ergy will be at­trib­uted to elec­tron $i$ and half to elec­tron ${\underline i}$, ac­count­ing for the fac­tor $\frac12$.

Fi­nally, there is the po­ten­tial en­ergy due to the nu­cleus-nu­cleus re­pul­sions,

$$V^{\rm NN}= {\textstyle\frac{1}{2}} \sum_{j=1}^J \sum_{\te... ...erline j}e^2}{4\pi\epsilon_0} \frac{1}{r_{j{\underline j}}}, %$$ (9.8)

where $r_{j{\underline j}}\equiv\vert{\skew0\vec r}^{\,\rm n}_j-{\skew0\vec r}^{\,\rm {n}}_{\underline j}\vert$ is the dis­tance be­tween nu­cleus num­ber $j$ and nu­cleus num­ber ${\underline j}$.

Solv­ing the full quan­tum prob­lem for this sys­tem of elec­trons and nu­clei ex­actly would in­volve find­ing the eigen­func­tions $\psi$ to the Hamil­ton­ian eigen­value prob­lem

$$\left[{\widehat T}^{\rm E}+ {\widehat T}^{\rm N}+ V^{\rm NE}+ V^{\rm EE}+ V^{\rm NN}\right] \psi = E \psi %$$ (9.9)

Here $\psi$ is a func­tion of the po­si­tion and spin co­or­di­nates of all the elec­trons and all the nu­clei, in other words:

$$\psi=\psi( {\skew0\vec r}_1,S_{z1}, {\skew0\vec r}_2,S_{z2... ...n}_{z2}, \ldots, {\skew0\vec r}^{\,\rm n}_J,S^{\rm n}_{zJ}) %$$ (9.10)

You might guess solv­ing this prob­lem is a tall or­der, and you would be per­fectly right. It can only be done an­a­lyt­i­cally for the very sim­plest case of one elec­tron and one nu­cleus. That is the hy­dro­gen atom so­lu­tion, us­ing an ef­fec­tive elec­tron mass to in­clude the nu­clear mo­tion. For any de­cent size sys­tem, an ac­cu­rate nu­mer­i­cal so­lu­tion is a for­mi­da­ble task too.

9.2.2 Ba­sic Born-Op­pen­heimer ap­prox­i­ma­tion

The gen­eral idea of the Born-Op­pen­heimer ap­prox­i­ma­tion is sim­ple. First note that the nu­clei are thou­sands of times heav­ier than the elec­trons. A pro­ton is al­most two thou­sand times heav­ier than an elec­tron, and that does not even count any neu­trons in the nu­clei.

So, if you take a look at the ki­netic en­ergy op­er­a­tors of the two,

$$\begin{eqnarray*} && {\widehat T}^{\rm E} = - \sum_{i=1}^I \frac{\hbar^2}{2m_{... ...}}^2} + \frac{\partial^2}{\partial {r^{\rm n}_{3j}}^2} \right) \end{eqnarray*}$$

then what would seem more rea­son­able than to ig­nore the ki­netic en­ergy ${\widehat T}^{\rm N}$ of the nu­clei? It has those heavy masses in the bot­tom.

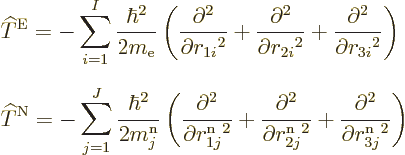
An al­ter­na­tive, and bet­ter, way of phras­ing the as­sump­tion that ${\widehat T}^{\rm N}$ can be ig­nored is to say that you ig­nore the un­cer­tainty in the po­si­tions of the nu­clei. For ex­am­ple, vi­su­al­ize the hy­dro­gen mol­e­cule, fig­ure 5.2. The two pro­tons, the nu­clei, have pretty well de­fined po­si­tions in the mol­e­cule, while the elec­tron wave func­tion ex­tends over the en­tire re­gion like a big blob of pos­si­ble mea­sur­able po­si­tions. So how im­por­tant could the un­cer­tainty in po­si­tion of the nu­clei re­ally be?

As­sum­ing that the nu­clei do not suf­fer from quan­tum un­cer­tainty in po­si­tion is re­ally equiv­a­lent to putting $\hbar$ to zero in their ki­netic en­ergy op­er­a­tor above, mak­ing the op­er­a­tor dis­ap­pear, be­cause $\hbar$ is na­ture’s mea­sure of un­cer­tainty. And with­out a ki­netic en­ergy term for the nu­clei, there is noth­ing left in the math­e­mat­ics to force them to have un­cer­tain po­si­tions. In­deed, you can now just guess nu­mer­i­cal val­ues for the po­si­tions of the nu­clei, and solve the ap­prox­i­mated eigen­value prob­lem $H\psi$ $\vphantom0\raisebox{1.5pt}{$=$}$ $E\psi$ for those as­sumed val­ues.

That thought is the Born-Op­pen­heimer ap­prox­i­ma­tion in a nut­shell. Just do the elec­trons, as­sum­ing suit­able po­si­tions for the nu­clei a pri­ori. The so­lu­tions that you get do­ing so will be called $\psi^{\rm E}$ to dis­tin­guish them from the true so­lu­tions $\psi$ that do not use the Born-Op­pen­heimer ap­prox­i­ma­tion. Math­e­mat­i­cally $\psi^{\rm E}$ will still be a func­tion of the elec­tron and nu­clear po­si­tions:

$$\psi^{\rm E}=\psi^{\rm E}( {\skew0\vec r}_1,S_{z1}, {\skew... ...}_{z2}, \ldots, {\skew0\vec r}^{\,\rm n}_J,S^{\rm n}_{zJ}). %$$ (9.11)

But phys­i­cally it will be a quite dif­fer­ent thing: it de­scribes the prob­a­bil­ity of find­ing the elec­trons, given the po­si­tions of the nu­clei. That is why there is a semi-colon be­tween the elec­tron po­si­tions and the nu­clear po­si­tions. The nu­clear po­si­tions are here as­sumed po­si­tions, while the elec­tron po­si­tions are po­ten­tial po­si­tions, for which the square mag­ni­tude of the wave func­tion $\psi^{\rm E}$ gives the prob­a­bil­ity. This is an elec­tron wave func­tion only.

In ap­pli­ca­tion, it is usu­ally most con­ve­nient to write the Hamil­ton­ian eigen­value prob­lem for the elec­tron wave func­tion as

$$\left[{\widehat T}^{\rm E}+ V^{\rm NE}+ V^{\rm EE}+ V^{\rm NN}\right] \psi^{\rm E} = (E^{\rm E}+ V^{\rm NN}) \psi^{\rm E},$$

which just means that the eigen­value is called $E^{\rm E}+V^{\rm NN}$ in­stead of sim­ply $E^{\rm E}$. The rea­son is that you can then get rid of $V^{\rm NN}$, and ob­tain the elec­tron wave func­tion eigen­value prob­lem in the more con­cise form

$$\fbox{$\displaystyle \left[{\widehat T}^{\rm E}+ V^{\rm NE}+ V^{\rm EE}\right] \psi^{\rm E}= E^{\rm E}\psi^{\rm E} $} %$$ (9.12)

Af­ter all, for given nu­clear co­or­di­nates, $V^{\rm NN}$ is just a both­er­some con­stant in the so­lu­tion of the elec­tron wave func­tion that you may just as well get rid of.

Of course, af­ter you com­pute your elec­tron eigen­func­tions, you want to get some­thing out of the re­sults. Maybe you are look­ing for the ground state of a mol­e­cule, like was done ear­lier for the hy­dro­gen mol­e­cule and mol­e­c­u­lar ion. In that case, the sim­plest ap­proach is to try out var­i­ous nu­clear po­si­tions and for each likely set of nu­clear po­si­tions com­pute the elec­tronic ground state en­ergy $E^{\rm E}_{\rm {gs}}$, the low­est eigen­value of the elec­tronic prob­lem (9.12) above.

For dif­fer­ent as­sumed nu­clear po­si­tions, you will get dif­fer­ent val­ues for the elec­tronic ground state en­ergy, and the nu­clear po­si­tions cor­re­spond­ing to the ac­tual ground state of the mol­e­cule will be the ones for which the to­tal en­ergy is least:

$$\fbox{$\displaystyle \mbox{nominal ground state condition: } E^{\rm E}_{\rm gs}+V^{\rm NN} \mbox{ is minimal} $} %$$ (9.13)

This is what was used to solve the hy­dro­gen mol­e­cule cases dis­cussed in ear­lier chap­ters; a com­puter pro­gram was writ­ten to print out the en­ergy $E^{\rm E}_{\rm {gs}}+V^{\rm NN}$ for a lot of dif­fer­ent spac­ings be­tween the nu­clei, al­low­ing the spac­ing that had the low­est to­tal en­ergy to be found by skim­ming down the print-out. That iden­ti­fied the ground state. The biggest er­ror in those cases was not in us­ing the Born-Op­pen­heimer ap­prox­i­ma­tion or the nom­i­nal ground state con­di­tion above, but in the crude way in which the elec­tron wave func­tion for given nu­clear po­si­tions was ap­prox­i­mated.

For more ac­cu­rate work, the nom­i­nal ground state con­di­tion (9.13) above does have big lim­i­ta­tions, so the next sub­sec­tion dis­cusses a more ad­vanced ap­proach.

9.2.3 Go­ing one bet­ter

Solv­ing the wave func­tion for elec­trons only, given po­si­tions of the nu­clei is def­i­nitely a big sim­pli­fi­ca­tion. But iden­ti­fy­ing the ground state as the po­si­tion of the nu­clei for which the elec­tron en­ergy plus nu­clear re­pul­sion en­ergy is min­i­mal is much less than ideal.

Such a pro­ce­dure ig­nores the mo­tion of the nu­clei, so it is no use for fig­ur­ing out any mol­e­c­u­lar dy­nam­ics be­yond the ground state. And even for the ground state, it is re­ally wrong to say that the nu­clei are at the po­si­tion of min­i­mum en­ergy, be­cause the un­cer­tainty prin­ci­ple does not al­low pre­cise po­si­tions for the nu­clei.

In­stead, the nu­clei be­have much like the par­ti­cle in a har­monic os­cil­la­tor. They are stuck in an elec­tron blob that wants to push them to their nom­i­nal po­si­tions. But un­cer­tainty does not al­low that, and the wave func­tion of the nu­clei spreads out a bit around the nom­i­nal po­si­tions, adding both ki­netic and po­ten­tial en­ergy to the mol­e­cule. One ex­am­ple ef­fect of this “zero point en­ergy” is to lower the re­quired dis­so­ci­a­tion en­ergy a bit from what you would ex­pect oth­er­wise.

It is not a big ef­fect, maybe on the or­der of tenths of elec­tron volts, com­pared to typ­i­cal elec­tron en­er­gies de­scribed in terms of mul­ti­ple elec­tron volts (and much more for the in­ner elec­trons in all but the light­est atoms.) But it is not as small as might be guessed based on the fact that the nu­clei are at least thou­sands of times heav­ier than the elec­trons.

More­over, though rel­a­tively small in en­ergy, the mo­tion of the nu­clei may ac­tu­ally be the one that is phys­i­cally the im­por­tant one. One rea­son is that the elec­trons tend to get stuck in sin­gle en­ergy states. That may be be­cause the dif­fer­ences be­tween elec­tron en­ergy lev­els tend to be so large com­pared to a typ­i­cal unit $\frac12kT$ of ther­mal en­ergy, about one hun­dredth of an elec­tron volt, or oth­er­wise be­cause they tend to get stuck in states for which the next higher en­ergy lev­els are al­ready filled with other elec­trons. The in­ter­est­ing phys­i­cal ef­fects then be­come due to the seem­ingly mi­nor nu­clear mo­tion.

For ex­am­ple, the heat ca­pac­ity of typ­i­cal di­atomic gases, like the hy­dro­gen mol­e­cule or air un­der nor­mal con­di­tions, is not in any di­rect sense due to the elec­trons; it is ki­netic en­ergy of trans­la­tion of the mol­e­cules plus a com­pa­ra­ble en­ergy due to an­gu­lar mo­men­tum of the mol­e­cule; read, an­gu­lar mo­tion of the nu­clei around their mu­tual cen­ter of grav­ity. The heat ca­pac­ity of solids too is largely due to nu­clear mo­tion, as is the heat con­duc­tion of non met­als.

For all those rea­sons, you would re­ally, re­ally, like to ac­tu­ally com­pute the mo­tion of the nu­clei, rather than just claim they are at fixed points. Does that mean that you need to go back and solve the com­bined wave func­tion for the com­plete sys­tem of elec­trons plus nu­clei any­way? Throw away the Born-Op­pen­heimer ap­prox­i­ma­tion re­sults?

For­tu­nately, the an­swer is mostly no. It turns out that na­ture is quite co­op­er­a­tive here, for a change. Af­ter you have done the elec­tronic struc­ture com­pu­ta­tions for all rel­e­vant po­si­tions of the nu­clei, you can pro­ceed with com­put­ing the mo­tion of nu­clei as a sep­a­rate prob­lem. For ex­am­ple, if you are in­ter­ested in the ground state nu­clear mo­tion, it is gov­erned by the Hamil­ton­ian eigen­value prob­lem

$$\left[{\widehat T}^{\rm N}+ V^{\rm NN}+ E^{\rm E}_1\right] \psi^{\rm N}_1 = E \psi^{\rm N}_1$$

where $\psi^{\rm N}_1$ is a wave func­tion in­volv­ing the nu­clear co­or­di­nates only, not any elec­tronic ones. The trick is in the po­ten­tial en­ergy to use in such a com­pu­ta­tion; it is not just the po­ten­tial en­ergy of nu­cleus to nu­cleus re­pul­sions, but you must in­clude an ad­di­tional en­ergy $E^{\rm E}_1$.

So, what is this $E^{\rm E}_1$? Easy, it is the elec­tronic ground state en­ergy $E^{\rm E}_{\rm {gs}}$ that you com­puted for as­sumed po­si­tions of the nu­clei. So it will de­pend on where the nu­clei are, but it does not de­pend on where the elec­trons are. You can just com­puted $E^{\rm E}_1$ for a suf­fi­cient num­ber of rel­e­vant nu­clear po­si­tions, tab­u­late the re­sults some­how, and in­ter­po­late them as needed. $E^{\rm E}_1$ is then a known func­tion func­tion of the nu­clear po­si­tions and so is $V^{\rm NN}$. Pro­ceed to solve for the wave func­tion for the nu­clei $\psi^{\rm N}_1$ as a prob­lem not di­rectly in­volv­ing any elec­trons.

And it does not nec­es­sar­ily have to be just to com­pute the ground state. You might want to study ther­mal mo­tion or what­ever. As long as the elec­trons are not kicked strongly enough to raise them to the next en­ergy level, you can as­sume that they are in their ground state, even if the nu­clei are not. The usual way to ex­plain this is to say some­thing like that the elec­trons “move so fast com­pared to the slow nu­clei that they have all the time in the world to ad­just them­selves to what­ever the elec­tronic ground state is for the cur­rent nu­clear po­si­tions.“

You might even de­cide to use clas­si­cal mol­e­c­u­lar dy­nam­ics based on the po­ten­tial $V^{\rm NN}+E^{\rm E}_1$ in­stead of quan­tum me­chan­ics. It would be much faster and eas­ier, and the re­sults are of­ten good enough.

So what if you are in­ter­ested in what your mol­e­cule is do­ing when the elec­trons are at an el­e­vated en­ergy level, in­stead of in their ground state? Can you still do it? Sure. If the elec­trons are in an el­e­vated en­ergy level $E^{\rm E}_n$, (for sim­plic­ity, it will be as­sumed that the elec­tron en­ergy lev­els are num­bered with a sin­gle in­dex $n$,) just solve

$$\fbox{$\displaystyle \left[{\widehat T}^{\rm N}+ V^{\rm NN}+ E^{\rm E}_n\right] \psi^{\rm N}_n = E \psi^{\rm N}_n $} %$$ (9.14)

or equiv­a­lent.

Note that for a dif­fer­ent value of $n$, this is truly a dif­fer­ent mo­tion prob­lem for the nu­clei, since the po­ten­tial en­ergy will be dif­fer­ent. If you are a vi­sual sort of per­son, you might vaguely vi­su­al­ize the po­ten­tial en­ergy for a given value of $n$ plot­ted as a sur­face in some high-di­men­sion­al space, and the state of the nu­clei mov­ing like a roller-coaster along that po­ten­tial en­ergy sur­face, speed­ing up when the sur­face goes down, slow­ing down if it goes up. There is one such sur­face for each value of $n$. Any­way. The bot­tom line is that peo­ple re­fer to these dif­fer­ent po­ten­tial en­er­gies as “po­ten­tial en­ergy sur­faces.” They are also called “adi­a­batic sur­faces” be­cause adi­a­batic nor­mally means processes suf­fi­ciently fast that heat trans­fer can be ig­nored. So, some quan­tum physi­cists fig­ured that it would be a good idea to use the same term for quan­tum processes that are so slow that quasi-equi­lib­rium con­di­tions per­sist through­out, and that have noth­ing to do with heat trans­fer.

Of course, any ap­prox­i­ma­tion can fail. It is pos­si­ble to get into trou­ble solv­ing your prob­lem for the nu­clei as ex­plained above. The dif­fi­cul­ties arise if two elec­tron en­ergy lev­els, call them $E^{\rm E}_n$ and $E^{\rm E}_{\underline n}$, be­come al­most equal, and in par­tic­u­lar when they cross. In sim­ple terms, the dif­fi­culty is that if en­ergy lev­els are equal, the en­ergy eigen­func­tions are not unique, and the slight­est thing can throw you from one eigen­func­tion to the com­pletely dif­fer­ent one.

You might now get alarmed, be­cause for ex­am­ple the hy­dro­gen mol­e­c­u­lar ion does have two dif­fer­ent ground state so­lu­tions with the same en­ergy. Its sin­gle elec­tron can be in ei­ther the spin-up state or the spin down state, and it does not make any dif­fer­ence for the en­ergy be­cause the as­sumed Hamil­ton­ian does not in­volve spin. In fact, all sys­tems with an odd num­ber of elec­trons will have a sec­ond so­lu­tion with all spins re­versed and the same en­ergy {D.50}. There is no need to worry, though; these re­versed-spin so­lu­tions go their own way and do not af­fect the va­lid­ity of (9.14). It is spa­tial, rather than spin nonunique­ness that is a con­cern.

There is a de­riva­tion of the nu­clear eigen­value prob­lem (9.14) in de­riva­tion {D.51}, show­ing what the ig­nored terms are and why they can usu­ally be ig­nored.