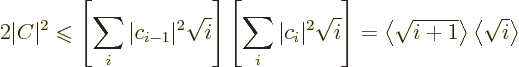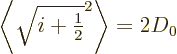| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.40 Quantization of radiation derivations
This gives various derivations for the addendum of the same name.
It is to be shown first that
To see that, note from (A.157) that
so the left-hand integral becomes
Now the curl, 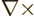 , is Hermitian,
{D.10}, so the second curl can be pushed in front of
the first curl. Then curl curl acts as
, is Hermitian,
{D.10}, so the second curl can be pushed in front of
the first curl. Then curl curl acts as 
 because
because
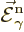 is solenoidal and the standard vector identity
(D.1). And the eigenvalue problem turns
is solenoidal and the standard vector identity
(D.1). And the eigenvalue problem turns 
 into
into 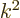 .
.
Note incidentally that the additional surface integral in
{D.10} is zero even for the photon modes of definite
angular momentum, {A.21.7}, because for them either
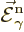 is zero on the surface or
is zero on the surface or


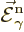 is. Also note that the integrals
become equal instead of opposite if you push complex conjugates on the
first factors in the integrands.
is. Also note that the integrals
become equal instead of opposite if you push complex conjugates on the
first factors in the integrands.
Now the Hamiltonian can be worked out. Using Using (A.152)
and (A.162), it is
When that is multiplied out and integrated, the 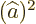 and
and 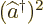 terms drop out because of (1). The remaining multiplied-out terms in
the Hamiltonian produce the stated Hamiltonian after noting the wave
function normalization (A.158).
terms drop out because of (1). The remaining multiplied-out terms in
the Hamiltonian produce the stated Hamiltonian after noting the wave
function normalization (A.158).
The final issue is to identify the relationships between the
coefficients 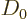 ,
, 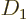 and
and 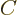 as given in the text. The
most important question is here under what circumstances
as given in the text. The
most important question is here under what circumstances 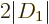 and
and
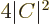 can get very close to the larger value
can get very close to the larger value 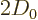 .
.
The coefficient 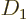 was defined as
was defined as
To estimate this, consider the infinite-dimensional vectors 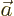 and
and 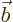 with coefficients
with coefficients
Note that 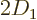 above is the inner product of these two vectors. And
an inner product is less in magnitude than the product of the lengths
of the vectors involved.
above is the inner product of these two vectors. And
an inner product is less in magnitude than the product of the lengths
of the vectors involved.
By changing the notations for the summation indices, (letting
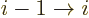 and
and 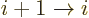 ), the sums become the expectation values
of
), the sums become the expectation values
of  , respectively
, respectively  . So
. So
The final equality is by the definition of 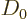 . The second
inequality already implies that
. The second
inequality already implies that 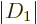 is always smaller than
is always smaller than
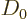 . However, if the expectation value of
. However, if the expectation value of  is large, it
does not make much of a difference.
is large, it
does not make much of a difference.
In that case, the bigger problem is the inner product between the
vectors 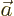 and
and 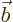 . Normally it is smaller than
the product of the lengths of the vectors. For it to become equal,
the two vectors have to be proportional. The coefficients of
. Normally it is smaller than
the product of the lengths of the vectors. For it to become equal,
the two vectors have to be proportional. The coefficients of
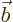 must be some multiple, call it
must be some multiple, call it 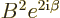 , of
those of
, of
those of 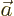 :
:
For larger values of  the square roots are about the same. Then
the above relationship requires an exponential decay of the
coefficients. For small values of
the square roots are about the same. Then
the above relationship requires an exponential decay of the
coefficients. For small values of  , obviously the above
relation cannot be satisfied. The needed values of
, obviously the above
relation cannot be satisfied. The needed values of 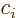 for negative
for negative
 do not exist. To reduce the effect of this
do not exist. To reduce the effect of this
start-up
problem, significant coefficients will have
to exist for a considerable range of  values.
values.
In addition to the above conditions, the coefficient 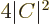 has to
be close to
has to
be close to 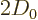 . Here the coefficient
. Here the coefficient 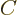 was defined as
was defined as
Using the same manipulations as for 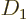 , but with
, but with
gives
To bound this further, define
By expanding the square root in a Taylor series,
where 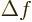 is the expectation value of the linear term in the
Taylor series; the inequalities express that a square root function
has a negative second order derivative. Multiplying these two
expressions shows that
is the expectation value of the linear term in the
Taylor series; the inequalities express that a square root function
has a negative second order derivative. Multiplying these two
expressions shows that
Since it has already been shown that the expectation value of  must
be large, this inequality will be almost an equality, anyway.
must
be large, this inequality will be almost an equality, anyway.
In any case,
This is less than
The big question is now how much it is smaller. To answer that,
use the shorthand
where  is the expectation value of the square root and
is the expectation value of the square root and  is
the deviation from the average. Then, noting that the expectation
value of
is
the deviation from the average. Then, noting that the expectation
value of  is zero,
is zero,
The second-last term is the bound for 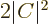 as obtained above. So,
the only way that
as obtained above. So,
the only way that 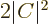 can be close to
can be close to 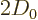 is if the final term
is relatively small. That means that the deviation from the
expectation square root must be relatively small. So the coefficients
is if the final term
is relatively small. That means that the deviation from the
expectation square root must be relatively small. So the coefficients
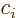 can only be significant in some limited range around an average
value of
can only be significant in some limited range around an average
value of  . In addition, for the vectors
. In addition, for the vectors 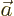 and
and
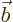 in the earlier estimate for
in the earlier estimate for 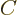 to be almost proportional,
to be almost proportional,
where 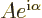 is some constant. That again means an
exponential dependence, like for the condition on
is some constant. That again means an
exponential dependence, like for the condition on 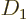 . And
. And
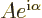 will have to be approximately
will have to be approximately  .
And
.
And  will have to be about 1, because otherwise start and end
effects will dominate the exponential part. That gives the situation
as described in the text.
will have to be about 1, because otherwise start and end
effects will dominate the exponential part. That gives the situation
as described in the text.
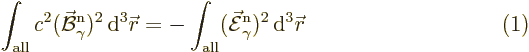
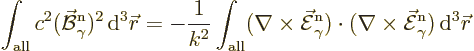
![]()
![]()
![]()
![]()
![\begin{displaymath}
H = {\textstyle\frac{1}{4}} \epsilon_0 \int_{\rm all} \left...
...cal B}_\gamma^{\rm {n}*})^2
\right] {\,\rm d}^3{\skew0\vec r}
\end{displaymath}](img6659.gif)
![]() ,
,![]()
![]()
![]()
![]()
![]() .
.![]()
![\begin{displaymath}
\vert 2D_1\vert = \vert{\left\langle\vec a\right.\hspace{-\...
...}\vert^2i\right]\left[\sum_i \vert c_{i+1}\vert^2(i+1)\right]}
\end{displaymath}](img6668.gif)
![]()
![]() .
.![]()
![]() ,
,![]() :
:![]()
![]() .
.![]()