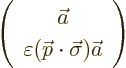| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.70 Emergence of spin from relativity
This note will give a (relatively) simple derivation of the Dirac
equation to show how relativity naturally gives rise to spin. The
equation will be derived without ever mentioning the word spin while
doing it, just to prove it can be done. Only Dirac’s assumption
that Einstein's square root disappears,
will be used and a few other assumptions that have nothing to do with
spin.
The conditions on the coefficient matrices 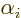 for the linear
combination to equal the square root can be found by squaring both
sides in the equation above and then comparing sides. They turn out to be:
for the linear
combination to equal the square root can be found by squaring both
sides in the equation above and then comparing sides. They turn out to be:
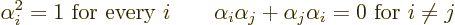 |
(D.45) |
Now assume that the matrices 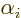 are Hermitian, as appropriate
for measurable energies, and choose to describe the wave function
vector in terms of the eigenvectors of matrix
are Hermitian, as appropriate
for measurable energies, and choose to describe the wave function
vector in terms of the eigenvectors of matrix 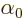 . Under
those conditions
. Under
those conditions 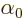 will be a diagonal matrix, and its
diagonal elements must be
will be a diagonal matrix, and its
diagonal elements must be  for its square to be the unit matrix.
So, choosing the order of the eigenvectors suitably,
for its square to be the unit matrix.
So, choosing the order of the eigenvectors suitably,
where the sizes of the positive and negative unit matrices in
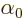 are still undecided; one of the two could in principle be
of zero size.
are still undecided; one of the two could in principle be
of zero size.
However, since  must be zero for
the three other Hermitian
must be zero for
the three other Hermitian 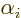 matrices, it is seen from
multiplying that out that they must be of the form
matrices, it is seen from
multiplying that out that they must be of the form
The 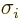 matrices, whatever they are, must be square in size
or the
matrices, whatever they are, must be square in size
or the 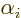 matrices would be singular and could not square to
one. This then implies that the positive and negative unit matrices
in
matrices would be singular and could not square to
one. This then implies that the positive and negative unit matrices
in 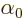 must be the same size.
must be the same size.
Now try to satisfy the remaining conditions on 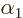 ,
,
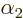 , and
, and 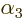 using just complex numbers, rather
than matrices, for the
using just complex numbers, rather
than matrices, for the 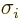 . By multiplying out the
conditions (D.45), you see that
. By multiplying out the
conditions (D.45), you see that
The first condition above would require each 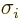 to be a number
of magnitude one, in other words, a number that can be written as
to be a number
of magnitude one, in other words, a number that can be written as
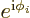 for some real angle
for some real angle 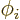 . The second
condition is then according to the Euler formula (2.5)
equivalent to the requirement that
. The second
condition is then according to the Euler formula (2.5)
equivalent to the requirement that
this implies that all three angles would have to be 90 degrees apart.
That is impossible: if 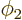 and
and  are each 90 degrees apart
from
are each 90 degrees apart
from 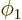 , then
, then 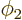 and
and  are either the same or
apart by 180 degrees; not by 90 degrees.
are either the same or
apart by 180 degrees; not by 90 degrees.
It follows that the components 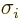 cannot be numbers, and must
be matrices too. Assume, reasonably, that they correspond to some
measurable quantity and are Hermitian. In that case the conditions
above on the
cannot be numbers, and must
be matrices too. Assume, reasonably, that they correspond to some
measurable quantity and are Hermitian. In that case the conditions
above on the 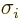 are the same as those on the
are the same as those on the 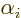 ,
with one critical difference: there are only three
,
with one critical difference: there are only three 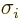 matrices, not four. And so the analysis repeats.
matrices, not four. And so the analysis repeats.
Choose to describe the wave function in terms of the eigenvectors of
the 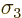 matrix; this does not conflict with the earlier choice
since all half wave function vectors are eigenvectors of the positive
and negative unit matrices in
matrix; this does not conflict with the earlier choice
since all half wave function vectors are eigenvectors of the positive
and negative unit matrices in 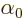 . So you have
. So you have
and the other two matrices must then be of the form
But now the components 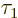 and
and 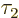 can indeed be just
complex numbers, since there are only two, and two angles can be apart
by 90 degrees. You can take
can indeed be just
complex numbers, since there are only two, and two angles can be apart
by 90 degrees. You can take 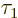

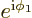 and then
and then
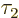

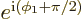 or
or
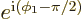 . The existence of two possibilities for
. The existence of two possibilities for
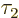 implies that on the wave function level, nature is not mirror
symmetric; momentum in the positive
implies that on the wave function level, nature is not mirror
symmetric; momentum in the positive  -direction interacts
differently with the
-direction interacts
differently with the  and
and  momenta than in the opposite
direction.
Since the observable effects are mirror symmetric, do not worry about
it and just take the first possibility.
momenta than in the opposite
direction.
Since the observable effects are mirror symmetric, do not worry about
it and just take the first possibility.
So, the goal of finding a formulation in which Einstein's square root
falls apart has been achieved. However, you can clean up some more,
by redefining the value of 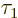 away. If the four-dimensional wave
function vector takes the form
away. If the four-dimensional wave
function vector takes the form 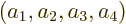 , define
, define
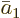

 ,
, 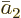

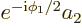 and similar for
and similar for 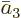 and
and
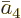 .
.
In that case, the final cleaned-up  matrices are
matrices are
 |
(D.46) |
The s
word has not been mentioned even once in this
derivation. So, now please express audible surprise that the
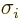 matrices turn out to be the Pauli (it can now be said) spin
matrices of chapter 12.10.
matrices turn out to be the Pauli (it can now be said) spin
matrices of chapter 12.10.
But there is more. Suppose you define a new coordinate system rotated
90 degrees around the  -axis. This turns the old
-axis. This turns the old  -axis into a
new
-axis into a
new  -axis. Since
-axis. Since 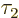 has an additional factor
has an additional factor
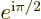 , to get the normalized coefficients, you must
include an additional factor
, to get the normalized coefficients, you must
include an additional factor 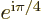 in
in 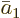 ,
which by the fundamental definition of angular momentum discussed in
addendum {A.19} means that it describes a state with
angular momentum
,
which by the fundamental definition of angular momentum discussed in
addendum {A.19} means that it describes a state with
angular momentum  . Similarly
. Similarly  corresponds
to a state with angular momentum
corresponds
to a state with angular momentum  and
and  and
and 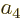 to ones with
to ones with 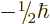 .
.
For nonzero momentum, the relativistic evolution of spin and momentum
becomes coupled. But still, if you look at the eigenstates of positive
energy, they take the form:
where  is a small number in the nonrelativistic limit and
is a small number in the nonrelativistic limit and
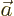 is the two-component vector
is the two-component vector  . The operator
corresponding to rotation of the coordinate system around the momentum
vector commutes with
. The operator
corresponding to rotation of the coordinate system around the momentum
vector commutes with 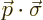 , hence the entire
four-dimensional vector transforms as a combination of a spin
, hence the entire
four-dimensional vector transforms as a combination of a spin
 state and a spin
state and a spin 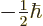 state for rotation
around the momentum vector.
state for rotation
around the momentum vector.
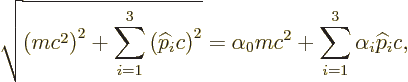
![]()
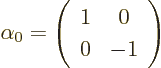
![]()
![]()
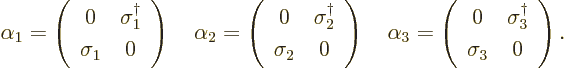
![]() ,
,![]() ,
,![]()
![]() .
.![]()
![]()
![]() ,
,![]()
![]()
![]() .
.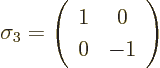
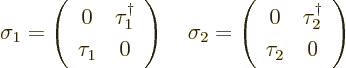
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]() .
.![]()

![]() -
-![]() -
-![]() -
-![]()
![]() ,
,![]()
![]() ,
,![]() .
.![]()
![]()
![]()
![]()
![]() .
.