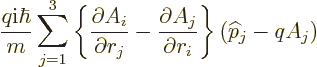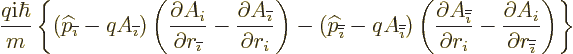| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.71 Electromagnetic commutators
The purpose of this note is to identify the two commutators of chapter
13.1; the one that produces the velocity (or rather,
the rate of change in expectation position), and the one that produces
the force (or rather the rate of change in expectation linear
momentum). All basic properties of commutators used in the
derivations below are described in chapter 4.5.4.
The Hamiltonian is
when the dot product is written out in index notation.
The rate of change in the expectation value of a position vector
component 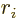 is according to chapter 7.2 given by
is according to chapter 7.2 given by
so you need the commutator
Now the term 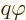 can be dropped, since functions of position
commute with each other. On the remainder, use the fact that each of
the two factors
can be dropped, since functions of position
commute with each other. On the remainder, use the fact that each of
the two factors 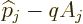 comes out at its own side of the
commutator, to give
comes out at its own side of the
commutator, to give
and then again, since the vector potential is just a function of
position too, the 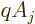 can be dropped from the commutators. What is
left is zero unless
can be dropped from the commutators. What is
left is zero unless  is the same as
is the same as  , since different
components of position and momentum commute, and when
, since different
components of position and momentum commute, and when 

 , it is minus the canonical commutator, (minus since the
order of
, it is minus the canonical commutator, (minus since the
order of 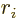 and
and 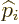 is inverted), and the canonical commutator
has value
is inverted), and the canonical commutator
has value 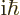 , so
, so
Plugging this in the time derivative of the expectation value of
position, you get
so the normal momentum 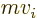 is indeed given by the operator
is indeed given by the operator
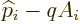 .
.
On to the other commutator! The  -th component of
Newton’s second law in expectation form,
-th component of
Newton’s second law in expectation form,
requires the commutator
The easiest is the term 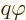 , since both
, since both  and
and
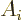 are functions of position and commute. And the commutator with
are functions of position and commute. And the commutator with
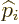 is the generalized fundamental operator of chapter
4.5.4,
is the generalized fundamental operator of chapter
4.5.4,
and plugging that into Newton’s equation, you can verify that the
electric field term of the Lorentz law has already been obtained.
In what is left of the desired commutator, again take each factor
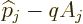 to its own side of the commutator:
to its own side of the commutator:
Work out the simpler commutator appearing here first:
the first equality because momentum operators and functions commute,
and the second equality is again the generalized fundamental
commutator.
Note that by assumption the derivatives of  are constants, so
the side of
are constants, so
the side of 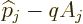 that this result appears is not relevant and
what is left of the Hamiltonian becomes
that this result appears is not relevant and
what is left of the Hamiltonian becomes
Now let 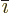 be the index following
be the index following  in the sequence
in the sequence
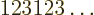 and
and 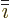 the one preceding it (or the second
following). Then the sum above will have a term where
the one preceding it (or the second
following). Then the sum above will have a term where 

 , but that term is seen to be zero, a term where
, but that term is seen to be zero, a term where 

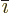 , and a term where
, and a term where 

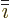 . The total is
then:
. The total is
then:
and that is
and the expression in brackets is the  -th component of
-th component of


 and produces the
and produces the
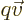

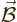 term in Newton’s equation provided that
term in Newton’s equation provided that
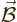



 .
.
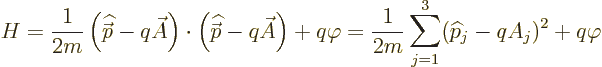
![]()
![\begin{displaymath}
\frac{{\rm d}\langle r_i \rangle}{{\rm d}t} =
\left\langle \frac{{\rm i}}{\hbar} [H,r_i] \right\rangle
\end{displaymath}](img7392.gif)
![\begin{displaymath}[H,r_i]= \left[\frac{1}{2m}\sum_{j=1}^3({\widehat p}_j-qA_j)^2+q\varphi,r_i\right]
\end{displaymath}](img7393.gif)
![\begin{displaymath}[H,r_i]= \frac{1}{2m}\sum_{j=1}^3
\bigg\{
({\widehat p}_j-q...
...r_i] + [{\widehat p}_j-qA_j,r_i]({\widehat p}_j-qA_j)
\bigg\}
\end{displaymath}](img7395.gif)
![]() -
-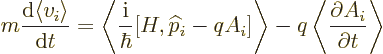
![\begin{displaymath}[H,{\widehat p}_i-qA_i]=
\left[\frac{1}{2m}\sum_{j=1}^3({\widehat p}_j-qA_j)^2+q\varphi,p_i-qA_i\right]
\end{displaymath}](img7401.gif)
![]() ,
,![]()
![]()
![]()
![\begin{displaymath}[q\varphi,p_i]={\rm i}\hbar q\frac{\partial\varphi}{\partial r_i}
\end{displaymath}](img7403.gif)
![]()
![\begin{displaymath}
\frac{1}{2m}
\sum_{j=1}^3
\bigg\{
({\widehat p}_j-qA_j)[...
...]+[{\widehat p}_j-qA_j,p_i-qA_i]({\widehat p}_j-qA_j)
\bigg\}
\end{displaymath}](img7404.gif)
![\begin{displaymath}[{\widehat p}_j-qA_j,p_i-qA_i]= - q [p_j,A_i] -q[A_j,p_i]
=
...
...artial r_j}
- {\rm i}\hbar q\frac{\partial A_j}{\partial r_i}
\end{displaymath}](img7405.gif)
![]()
![]()