|
|
|
|
|
Next: 6.21 Intro to Band Structure |
|
Some of the basic physics of electrical conduction in metals can be understood using a very simple model. That model is a free-electron gas, i.e. noninteracting electrons, in a periodic box.
The classical definition of electric current is moving charges. That can readily be converted to quantum terms for noninteracting electrons in a periodic box. The single-particle energy states for these electrons have definite velocity. That velocity is given by the linear momentum divided by the mass.
Consider the possibility of an electric current in a chosen
![]() -
-![]()
![]()
![]() -
-![]()
![]()
![]()
![]() -
-
In the system ground state, shown to the left in figure
6.18, no current will flow, because there are just as many
electrons that move toward negative ![]()
![]() .
.![]() -
-![]() -
-![]() -
-![]() -
-![]()
![]()
Note that the electrons must pick up a bit of additional energy when they are moved from states with negative velocity to states with positive velocity. That is because the Pauli exclusion principle forbids the electrons from entering the lower energy states of positive velocity that are already filled with electrons.
However, the required energy is small. You might just briefly turn on an external voltage source to produce an electric field that gets the electrons moving. Then you can turn off the voltage source again, because once set into motion, the noninteracting electrons will keep moving forever.
In physical terms, it is not really that just a few electrons make a
big velocity change from negative to positive due to the applied
voltage. In quantum mechanics electrons are completely
indistinguishable, and all the electrons are involved equally in the
changes of state. It is better to say that all electrons acquire a
small additional drift velocity ![]()
![]() -
-
The net result is still the energy versus velocity distribution shown to the right in figure 6.18. Electrons at the highest energy levels with positive velocities go up a bit in energy. Electrons at the highest energy levels with negative velocities go down a bit in energy. The electrons at lower energy levels move along to ensure that there is no more than one electron in each quantum state. The fact remains that the system of electrons picks up a bit of additional energy. (The last subsection of derivation {D.45} discusses the effect of the applied voltage in more detail.)
Conduction electrons in an actual metal wire behave similar to free
electrons. However, they must move around the metal atoms, which are
normally arranged in some periodic pattern called the crystal
structure. The conduction electrons will periodically get scattered
by thermal vibrations of the crystal structure, (in quantum terms, by
phonons), and by crystal structure imperfections and impurities. That
kills off their organized drift velocity ![]() ,
,collisions,
is called
the “free path” length ![]() .
.
Of course, that does not make much sense from a classical point of view. Common sense says that a point-size classical electron in a solid should pretty much bounce off every atom it encounters. Therefore the free path of the electrons should be of the order of a single atomic spacing, not thousands of atoms or much more still. However, in quantum mechanics electrons are not particles with a definite position. Electrons are described by a wave function. It turns out that electron waves can propagate through perfect crystals without scattering, much like electromagnetic waves can. The free-electron gas wave functions adapt to the crystal structure, allowing the electrons to flow past the atoms without reflection.
It is of some interest to compare the quantum picture of conduction to
that of a classical, nonquantum, description. In the classical
picture, all conduction electrons would have a random thermal motion.
The average velocity ![]()
![]() ,
,![]()
![]()
![]()
![]()
![]() -
-
Based on this picture, a ballpark expression for the classical
conductivity can be written down. First, by definition the current
density ![]()
![]() ,
,![]()
![]()
![]()
![]() -
-
| (6.30) |
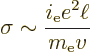 |
(6.31) |
For metals, things are a bit different because of quantum effects. In
metals random collisions are restricted to a small fraction of
electrons at the highest energy levels. These energy levels are
characterized by the Fermi energy, the highest occupied energy level
in the spectrum to the left in figure 6.18. Electrons of
lower energies do not have empty states nearby to be randomly
scattered into. The velocity of electrons near the Fermi energy is
much larger than the thermal value ![]() ,
,![]()
![]()
![]()
The classical picture works much better for semiconductors, since these have much less conduction electrons than would be needed to fill all the quantum states available at thermal energies. The mass correction remains required.
Key Points
- The free-electron gas can be used to understand conduction in metals in simple terms.
- In the absence of a net current the electrons are in states with velocities in all directions. The net electron motion therefore averages out to zero.
- A net current is achieved by giving the electrons an additional small organized motion.
- The energy needed to do this is small.
- In real metals, the electrons lose their organized motion due to collisions with phonons and crystal imperfections. Therefore a small permanent voltage must be applied to maintain the net motion. That means that there is electrical resistance. However, it is very small for typical metals.