6.22 Electrons in Crystals

A meaningful discussion of semiconductors requires some background on how electrons move through solids. The free-electron gas model simply assumes that the electrons move through an empty periodic box. But of course, to describe a real solid the box should really be filled with the countless atoms around which the conduction electrons move.

This subsection will explain how the motion of electrons gets modified by the atoms. To keep things simple, it will still be assumed that there is no direct interaction between the electrons. It will also be assumed that the solid is crystalline, which means that the atoms are arranged in a periodic pattern. The atomic period should be assumed to be many orders of magnitude shorter than the size of the periodic box. There must be many atoms in each direction in the box.

**Figure 6.21:** Potential energy seen by an electron along a line of nuclei. The potential energy is in green, the nuclei are in red.
$\begin{figure}\centering \epsffile{bwpotclmb.eps} \end{figure}$

The effect of the crystal is to introduce a periodic potential energy for the electrons. For example, figure 6.21 gives a sketch of the potential energy seen by an electron along a line of nuclei. Whenever the electron is right on top of a nucleus, its potential energy plunges. Close enough to a nucleus, a very strong attractive Coulomb potential is seen. Of course, on a line that does not pass exactly through nuclei, the potential will not plunge that low.

**Figure 6.22:** Potential energy seen by an electron in the one-dimensional simplified model of Kronig & Penney.
$\begin{figure}\centering \setlength{\unitlength}{1pt} \begin{picture}(380,53... ...-1,0){184}} \put(0,-10){\makebox(0,0)[b]{$\ell_x$}} \end{picture} \end{figure}$

Kronig & Penney developed a very simple one-dimensional model that explains much of the motion of electrons through crystals. It assumes that the potential energy seen by the electrons is periodic on some atomic-scale period

. It also assumes that this potential consists of square dips, like in figure 6.22. You might think of the regions of lowered potential energy as the immediate vicinity of the nuclei. This is the model that will be examined. The atomic period

is assumed to be much smaller than the periodic box size $\ell_x$ , i.e. the size of the complete crystal. In particular, the box should contain a large and whole number of atomic periods.

Three-dimensional Kronig & Penney quantum states can be formed as products of one-dimensional ones, compare chapter 3.5.8. However, such states are limited to potentials that are sums of one-dimensional ones. In any case, this section will restrict itself mostly to the one-dimensional case.

6.22.1 Bloch waves

This subsection examines the single-particle quantum states, or energy eigenfunctions, of electrons in one-dimensional solids.

For free electrons, the energy eigenfunctions were given in section 6.18. In one dimension they are:

$\begin{displaymath} \pp{n_x}/x/// = C e^{{\rm i}k_x x} \end{displaymath}$

To find the equivalent one-dimensional energy eigenfunctions $\pp{n_x}/x///$ in the presence of a crystal potential

is messy. It requires solution of the one-dimensional Hamiltonian eigenvalue problem

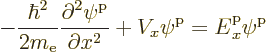
$\begin{displaymath} -\frac{\hbar^2}{2m_{\rm e}} \frac{\partial^2\psi^{\rm p}}{\... ...2} + V_x \psi^{\rm p} = {\vphantom' E}^{\rm p}_x \psi^{\rm p} \end{displaymath}$

However, it can be shown that the eigenfunctions can always be written in the form:

$\begin{displaymath} \fbox{$\displaystyle \pp{n_x}/x/// = \pp{{\rm p},n_x}/x/// e^{{\rm i}k_x x} $} % \end{displaymath}$

(6.32)

Energy eigenfunctions of the form (6.32) are called “Bloch waves.” It may be pointed out that this form of the energy eigenfunctions was discovered by Floquet, not Bloch. However, Floquet was a mathematician. In naming the solutions after Bloch instead of Floquet, physicists celebrate the physicist who could do it too, just half a century later.

The reason why the energy eigenfunctions take this form, and what it means for the electron motion are discussed further in chapter 7.10.5. There are only two key points of interest for now. First, the possible values of the wave number

are exactly the same as for the free-electron gas, given in (6.28). Otherwise the eigenfunction would not be periodic on the period of the box. Second, the electron velocity can be found by differentiating the single particle energy ${\vphantom' E}^{\rm p}_x$ with respect to the “crystal momentum” $p_{{\rm {cm}},x}$ $\vphantom0\raisebox{1.5pt}{$=$}$ ${\hbar}k_x$ . That is the same as for the free-electron gas. If you differentiate the one-dimensional free-electron gas kinetic energy ${\vphantom' E}^{\rm p}_x$ $\vphantom0\raisebox{1.5pt}{$=$}$ $({\hbar}k_x)^2$ $\raisebox{.5pt}{$/$}$ $2m_{\rm e}$ with respect to

$\vphantom0\raisebox{1.5pt}{$=$}$ ${\hbar}k_x$ , you get the velocity.

6.22.2 Example spectra

As the previous section discussed, the difference between metals and insulators is due to differences in their energy spectra. The one-dimensional Kronig & Penney model can provide some insight into it.

**Figure 6.23:** Example Kronig & Penney spectra.
$\begin{figure}\centering \setlength{\unitlength}{1pt} \begin{picture}(405,20... ...tor}} \put(135,0){\makebox(0,0)[b]{free electrons}} \end{picture} \end{figure}$

Finding the energy eigenvalues is not difficult on a computer, {N.9}. A couple of example spectra are shown in figure 6.23. The vertical coordinate is the single-electron energy, as usual. The horizontal coordinate is the electron velocity. (So the free electron example is the one-dimensional version of the spectrum in figure 6.18, but the axes are much more compressed here.) Quantum states occupied by electrons are again in red.

The example to the left in figure 6.23 tries to roughly model a metal like lithium. The depth of the potential drops in figure 6.22 was chosen so that for lone atoms, (i.e. for widely spaced potential drops), there is one bound spatial state and a second marginally bound state. You might think of the bound state as holding lithium’s two inner 1s electrons, and the marginally bound state as holding its loosely bound single 2s valence electron.

Note that the 1s state is just a red dot in the lower part of the left spectrum in figure 6.23. The energy of the inner electrons is not visibly affected by the neighboring atoms. Also, the velocity does not budge from zero; electrons in the inner states would hardly move even if there were unfilled states. These two observations are related, because as mentioned earlier, the velocity is the derivative of the energy with respect to the crystal momentum. If the energy does not vary, the velocity is zero.

The second energy level has broadened into a half-filled conduction band. Like for the free-electron gas in figure 6.18, it requires little energy to move some Fermi-level electrons in this band from negative to positive velocities to achieve net electrical conduction.

The spectrum in the middle of figure 6.23 tries to roughly model an insulator like diamond. (The one-dimensional model is too simple to model an alkaline metal with two valence electrons like beryllium. The spectra of these metals involve different energy bands that merge together, and merging bands do not occur in the one-dimensional model.) The voltage drops have been increased a bit to make the second energy level for lone atoms more solidly bound. And it has been assumed that there are now four electrons per atom, so that the second band is completely filled.

Now the only way to achieve net electrical conduction is to move some electrons from the filled valence band to the empty conduction band above it. That requires much more energy than a normal applied voltage could provide. So the crystal is an insulator.

The reasons why the spectra look as shown in figure 6.23 are not obvious. Note {N.9} explains by example what happens to the free-electron gas energy eigenfunctions when there is a crystal potential. A much shorter explanation that hits the nail squarely on the head is “That is just the way the Schrödinger equation is.”

6.22.3 Effective mass

The spectrum to the right in figure 6.23 shows the one-dimensional free-electron gas. The relationship between velocity and energy is given by the classical expression for the kinetic energy in the

-direction:

$\begin{displaymath} {\vphantom' E}^{\rm p}_x = {\textstyle\frac{1}{2}} m_{\rm e}{v^{\rm p}_x}^2 \end{displaymath}$

It is interesting to compare this spectrum to that of the metal to the left in figure 6.23. The occupied part of the conduction band of the metal is approximately parabolic just like the free-electron gas spectrum. To a fair approximation, in the occupied part of the conduction band

$\begin{displaymath} {\vphantom' E}^{\rm p}_x - {\vphantom' E}^{\rm p}_{{\rm c},x} = {\textstyle\frac{1}{2}} m_{{\rm eff},x} {v^{\rm p}_x}^2 \end{displaymath}$

This illustrates that conduction band electrons in metals behave much like free electrons. And the similarity to free electrons becomes even stronger if you define the zero level of energy to be at the bottom of the conduction band and replace the true electron mass by an effective mass. For the metal shown in figure 6.23, the effective mass is 61% of the true electron mass. That makes the parabola somewhat flatter than for the free-electron gas. For electrons that reach the conduction band of the insulator in figure 6.23, the effective mass is only 18% of the true mass.

In previous sections, the valence electrons in metals were repeatedly approximated as free electrons to derive such properties as degeneracy pressure and thermionic emission. The justification was given that the forces on the valence electrons tend to come from all directions and average out. But as the example above now shows, that approximation can be improved upon by replacing the true electron mass by an effective mass. For the valence electrons in copper, the appropriate effective mass is about one and a half times the true electron mass, [42, p. 257]. So the use of the true electron mass in the examples was not dramatically wrong.

And the agreement between conduction band electrons and free electrons is even deeper than the similarity of the spectra indicates. You can also use the density of states for the free-electron gas, as given in section 6.3, if you substitute in the effective mass.

To see why, assume that the relationship between the energy ${\vphantom' E}^{\rm p}_x$ and the velocity $v^{\rm {p}}_x$ is the same as that for a free-electron gas whose electrons have the appropriate effective mass. Then so is the relationship between the energy ${\vphantom' E}^{\rm p}_x$ and the wave number

the same as for that electron gas. That is because the velocity is merely the derivative of ${\vphantom' E}^{\rm p}_x$ with respect to ${\hbar}k_x$ . You need the same ${\vphantom' E}^{\rm p}_x$ versus

relation to get the same velocity. (This assumes that you measure both the energy and the wave number from the location of minimum conduction band energy.) And if the ${\vphantom' E}^{\rm p}_x$ versus

relation is the same as for the free-electron gas, then so is the density of states. That is because the quantum states have the same wave number spacing regardless of the crystal potential.

It should however be pointed out that in three dimensions, things get messier. Often the effective masses are different in different crystal directions. In that case you need to define some suitable average to use the free-electron gas density of states. In addition, for typical semiconductors the energy structure of the holes at the top of the valence band is highly complex.

6.22.4 Crystal momentum

The crystal momentum of electrons in a solid is not the same as the linear momentum of free electrons. However, it is similarly important. It is related to optical properties such as the difference between direct and indirect gap semiconductors. Because of this importance, spectra are usually plotted against the crystal momentum, rather than against the electron velocity. The Kronig & Penney model provides a simple example to explain some of the ideas.

**Figure 6.24:** Spectrum against wave number in the extended zone scheme.
$\begin{figure}\centering \setlength{\unitlength}{1pt} \begin{picture}(400,20... ...tor}} \put(100,0){\makebox(0,0)[b]{free electrons}} \end{picture} \end{figure}$

Figure 6.24 shows the single-electron energy plotted against the crystal momentum. Note that this is equivalent to a plot against the wave number

; the crystal momentum is just a simple multiple of the wave number, $p_{{\rm {cm}},x}$ $\vphantom0\raisebox{1.5pt}{$=$}$ ${\hbar}k_x$ . The figure has nondimensionalized the wave number by multiplying it by the atomic period

. Both the example insulator and the free-electron gas are shown in the figure.

$\begin{displaymath} \pp{n_x}/x/// = \pp{{\rm p},n_x}/x/// e^{{\rm i}k_x x} \end{displaymath}$

Therefore there is a problem with how to define a unique value of

. There are different solutions to this problem. Figure 6.24 follows the so-called “extended zone scheme.” It takes the wave number to be zero at the minimum energy and then keeps increasing the magnitude with energy. This is a good scheme for the free-electron gas. It also works nicely if the potential is so weak that the energy states are almost the free-electron gas ones.

**Figure 6.25:** Spectrum against wave number in the reduced zone scheme.
$\begin{figure}\centering \setlength{\unitlength}{1pt} \begin{picture}(400,20... ...tor}} \put(100,0){\makebox(0,0)[b]{free electrons}} \end{picture} \end{figure}$

A second approach is much more common, though. It uses the indeterminacy in

to shift it into the range $\vphantom{0}\raisebox{1.5pt}{$-$}$ $\pi$ $\raisebox{-.3pt}{$\leqslant$}$

$\raisebox{-.3pt}{$\leqslant$}$ $\pi$ . That range is called the “first Brillouin zone.” Restricting the wave numbers to the first Brillouin zone produces figure 6.25. This is called the “reduced zone scheme.” Esthetically, it is clearly an improvement in case of a nontrivial crystal potential.

But it is much more than that. For one, the different energy curves in the reduced zone scheme can be thought of as modified atomic energy levels of lone atoms. The corresponding Bloch waves can be thought of as modified atomic states, modulated by a relatively slowly varying exponential $e^{{{\rm i}}k_xx}$ .

Second, the reduced zone scheme is important for optical applications of semiconductors. In particular,

To see why that is important, suppose that you want to use a semiconductor to create light. To achieve that, you need to somehow excite electrons from the valence band to the conduction band. How to do that will be discussed in section 6.27.7. The question here is what happens next. The excited electrons will eventually drop back into the valence band. If all is well, they will emit the energy they lose in doing so as a photon. Then the semiconductor will emit light.

**Figure 6.26:** Some one-dimensional energy bands for a few basic semiconductors.
$\begin{figure}\centering \setlength{\unitlength}{1pt} \begin{picture}(405,10... ...10,55){\line(0,1){4}} \put(351,55){\line(-1,0){41}} \end{picture} \end{figure}$

It turns out that the excited electrons are mostly in the lowest energy states in the conduction band. For various reasons. that tends to be true despite the absence of thermal equilibrium. They are created there or evolve to it. Also, the holes that the excited electrons leave behind in the valence band are mostly at the highest energy levels in that band.

Now consider the energy bands of some actual semiconductors shown to the left in figure 6.26. In particular, consider the spectrum of gallium arsenide. The excited electrons are at the lowest point of the conduction band. That is at zero crystal momentum. The holes are at the highest point in the valence band, which is also at zero crystal momentum. Therefore, the excited electrons can drop vertically down into the holes. The crystal momentum does not change, it stays zero. There is no problem. In fact, the first patent for a light emitting diode was for a gallium arsenide one, in 1961. The energy of the emitted photons is given by the band gap of gallium arsenide, somewhat less than 1.5 eV. That is slightly below the visible range, in the near infrared. It is suitable for remote controls and other nonvisible applications.

But now consider germanium in figure 6.26. The highest point of the valence band is still at zero crystal momentum. But the lowest point of the conduction band is now at maximum crystal momentum in the reduced zone scheme. When the excited electrons drop back into the holes, their crystal momentum changes. Since crystal momentum is conserved, something else must account for the difference. And the photon does not have any crystal momentum to speak of. It is a phonon of crystal vibration that must carry off the difference in crystal momentum. Or supply the difference, if there are enough pre-existing thermal phonons. The required involvement of a phonon in addition to the photon makes the entire process much more cumbersome. Therefore the energy of the electron is much more likely to be released through some alternate mechanism that produces heat instead of light.

The situation for silicon is like that for germanium. However, the lowest energy in the conduction band occurs for a different direction of the crystal momentum. The spectrum for that direction of the crystal momentum is shown to the right in figure 6.26. It still requires a change in crystal momentum.

At the time of writing, there is a lot of interest in improving the light emission of silicon. The reason is its prevalence in semiconductor applications. If silicon itself can be made to emit light efficiently, there is no need for the complications of involving different materials to do it. One trick is to minimize processes that allow electrons to drop back into the valence band without emitting photons. Another is to use surface modification techniques that promote absorption of photons in solar cell applications. The underlying idea is that at least in thermal equilibrium, the best absorbers of electromagnetic radiation are also the best emitters, section 6.8.

Gallium arsenide is called a “direct-gap semiconductor” because the electrons can fall straight down into the holes. Silicon and germanium are called “indirect-gap semiconductors” because the electrons must change crystal momentum. Note that these terms are accurate and understandable, a rarity in physics.

Conservation of crystal momentum does not just affect the emission of light. It also affects its absorption. Indirect-gap semiconductors do not absorb photons very well if the photons have little more energy than the band gap. They absorb photons with enough energy to induce vertical electron transitions a lot better.

It may be noted that conservation of crystal momentum is often called “conservation of wave vector.” It is the same thing of course, since the crystal momentum is simply $\hbar$ times the wave vector. However, those pesky new students often have a fairly good understanding of momentum conservation, and the term momentum would leave them insufficiently impressed with the brilliance of the physicist using it.

(If you wonder why crystal momentum is preserved, and how it even can be if the crystal momentum is not unique, the answer is in the discussion of conservation laws in chapter 7.3 and its note. It is not really momentum that is conserved, but the product of the single-particle eigenvalues $e^{{{\rm i}}k_xd_x}$ of the operator that translates the system involved over a distance

. These eigenvalues do not change if the wave numbers change by a whole multiple of $2\pi$ $\raisebox{.5pt}{$/$}$

, so there is no violation of the conservation law if they do. For a system of particles in free space, the potential is trivial; then you can take

equal to zero to eliminate the ambiguity in

and so in the momentum. But for a nontrivial crystal potential,

is fixed. Also, since a photon moves so fast, its wave number is almost zero on the atomic scale, giving it negligible crystal momentum. At least it does for the photons in the eV range that are relevant here.)

**Figure 6.27:** Spectrum against wave number in the periodic zone scheme.
$\begin{figure}\centering \setlength{\unitlength}{1pt} \begin{picture}(300,20... ...{\rm p}_x$}} \put(0,0){\makebox(0,0)[b]{insulator}} \end{picture} \end{figure}$

Returning to the possible ways to plot spectra, the so-called “periodic zone scheme” takes the reduced zone scheme and extends it periodically, as in figure 6.27. That makes for very esthetic pictures, especially in three dimensions.

Of course, in three dimensions there is no reason for the spectra in the

and

directions to be the same as the one in the

-direction. Each can in principle be completely different from the other two. Regardless of the differences, valid three-dimensional Kronig & Penney energy eigenfunctions are obtained as the product of the

and

eigenfunctions, and their energy is the sum of the eigenvalues.

Similarly, typical spectra for real solids have to show the spectrum versus wave number for more than one crystal direction to be comprehensive. One example was for silicon in figure 6.26. A more complete description of the one-dimensional spectra of real semiconductors is given in the next subsection.

6.22.5 Three-dimensional crystals

A complete description of the theory of three-dimensional crystals is beyond the scope of the current discussion. Chapter 10 provides a first introduction. However, because of the importance of semiconductors such as silicon, germanium, and gallium arsenide, it may be a good idea to explain a few ideas already.

**Figure 6.28:** Schematic of the zinc blende (ZnS) crystal relevant to important semiconductors including silicon.
$\begin{figure}\centering \setlength{\unitlength}{1pt} \begin{picture}(400,21... ...,0)[bl]{Ga}} \put(-119,41){\makebox(0,0)[r]{As}} } \end{picture} \end{figure}$

Consider first a gallium arsenide crystal. Gallium arsenide has the same crystal structure as zinc sulfide, in the form known as zinc blende or sphalerite. The crystal is sketched in figure 6.28. The larger spheres represent the nuclei and inner electrons of the gallium atoms. The smaller spheres represent the nuclei and inner electrons of the arsenic atoms. Because arsenic has a more positively charged nucleus, it holds its electrons more tightly. The figure exaggerates the effect to keep the atoms visually apart.

The grey gas between these atom cores represents the valence electrons. Each gallium atom contributes 3 valence electrons and each arsenic atom contributes 5. That makes an average of 4 valence electrons per atom.

As the figure shows, each gallium atom core is surrounded by 4 arsenic ones and vice-versa. The grey sticks indicate the directions of the covalent bonds between these atom cores. You can think of these bonds as somewhat polar sp $\POW9,{3}$ hybrids. They are polar since the arsenic atom is more electronegative than the gallium one.

It is customary to think of crystals as being build up out of simple building blocks called “unit cells.” The conventional unit cells for the zinc blende crystal are the little cubes outlined by the thicker red lines in figure 6.28. Note in particular that you can find gallium atoms at each corner of these little cubes, as well as in the center of each face of them. That makes zinc blende an example of what is called a “face-centered cubic” lattice. For obvious reasons, everybody abbreviates that to FCC.

You can think of the unit cells as subdivided further into 8 half-size cubes, as indicated by the thinner red lines. There is an arsenic atom in the center of every other of these smaller cubes.

The simple one-dimensional Kronig & Penney model assumed that the crystal was periodic with a period

. For real three-dimensional crystals, there is not just one period, but three. More precisely, there are three so-called “primitive translation vectors” $\vec{d}_1$ , $\vec{d}_2$ , and $\vec{d}_3$ . A set of primitive translation vectors for the FCC crystal is shown in figure 6.28. If you move around by whole multiples of these vectors, you arrive at points that look identical to your starting point.

For example, if you start at the center of a gallium atom, you will again be at the center of a gallium atom. And you can step to whatever gallium atom you like in this way. At least as long as the whole multiples are allowed to be both positive and negative. In particular, suppose you start at the gallium atom with the Ga label in figure 6.28. Then $\vec{d}_1$ allows you to step to any other gallium atom on the same line going towards the right and left. Vector $\vec{d}_2$ allows you to step to the next or previous line in the same horizontal plane. And vector $\vec{d}_3$ allows you to step to the next higher or lower horizontal plane.

The choice of primitive translation vectors is not unique. In particular, many sources prefer to draw the vector $\vec{d}_1$ towards the gallium atom in the front face center rather than to the one at the right. That is more symmetric, but moving around with them gets harder to visualize. Then you would have to step over $\vec{d}_1$ , $\vec{d}_2$ , and $-\vec{d}_3$ just to reach the atom to the right.

You can use the primitive translation vectors also to mentally create the zinc blende crystal. Consider the pair of atoms with the Ga and As labels in figure 6.28. Suppose that you put a copy of this pair at every point that you can reach by stepping around with the primitive translation vectors. Then you get the complete zinc blende crystal. The pair of atoms is therefore called a “basis” of the zinc blende crystal.

This also illustrates another point. The choice of unit cell for a given crystal structure is not unique. In particular, the parallelepiped with the primitive translation vectors as sides can be used as an alternative unit cell. Such a unit cell has the smallest possible volume, and is called a primitive cell.

The crystal structure of silicon and germanium, as well as diamond, is identical to the zinc blende structure, but all atoms are of the same type. This crystal structure is appropriately called the diamond structure. The basis is still a two-atom pair, even if the two atoms are now the same. Interestingly enough, it is not possible to create the diamond crystal by distributing copies of a single atom. Not as long as you step around with only three primitive translation vectors.

For the one-dimensional Kronig & Penney model, there was only a single wave number

that characterized the quantum states. For a three-dimensional crystal, there is a three-dimensional wave number vector ${\vec k}$ with components

, and

. That is just like for the free-electron gas in three dimensions as discussed in earlier sections.

In the Kronig & Penney model, the wave numbers could be reduced to a finite interval

$\begin{displaymath} - \frac{\pi}{d_x} \mathrel{\raisebox{-.7pt}{$\leqslant$}}k_x < \frac{\pi}{d_x} \end{displaymath}$

**Figure 6.29:** First Brillouin zone of the FCC crystal.
$\begin{figure}\centering \setlength{\unitlength}{1pt} \begin{picture}(200,17... ...51){$k_z$} \put(70,62){$k_x$} \put(-22,154){$k_y$} \end{picture} \end{figure}$

In three dimensions, the first Brillouin zone is no longer a one-dimensional interval but a three-dimensional volume. And the separations over which wave number vectors are equivalent are no longer so simple. Instead of simply taking an inverse of the period

, as in $2\pi$ $\raisebox{.5pt}{$/$}$

, you have to take an inverse of the matrix formed by the three primitive translation vectors $\vec{d}_1$ , $\vec{d}_2$ , and $\vec{d}_3$ . Next you have to identify the wave number vectors closest to the origin that are enough to describe all quantum states. If you do all that for the FCC crystal, you will end up with the first Brillouin zone shown in figure 6.29. It is shaped like a cube with its 8 corners cut off.

The shape of the first Brillouin zone is important for understanding graphs of three-dimensional spectra. Every single point in the first Brillouin zone corresponds to multiple Bloch waves, each with its own energy. To plot all those energies is not possible; it would require a four-dimensional plot. Instead, what is done is plot the energies along representative lines. Such plots will here be indicated as one-dimensional energy bands. Note however that they are one-dimensional bands of true three-dimensional crystals. They are not just Kronig & Penney model bands.

Typical points between which one-dimensional bands are drawn are indicated in figure 6.29. You and I would probably name such points something like F (face), E (edge), and C (corner), with a clarifying subscript as needed. However, physicists come up with names like K, L, W, and X, and declare them standard. The center of the Brillouin zone is the origin, where the wave number vector is zero. Normal people would therefore indicate it as O or 0. However, physicists are not normal people. They indicate the origin by $\Gamma$ because the shape of this Greek letter reminds them of a gallows. Physicists just love gallows humor.

**Figure 6.30:** Sketch of a more complete spectrum of germanium. (Based on results of the VASP 5.2 commercial computer code.)
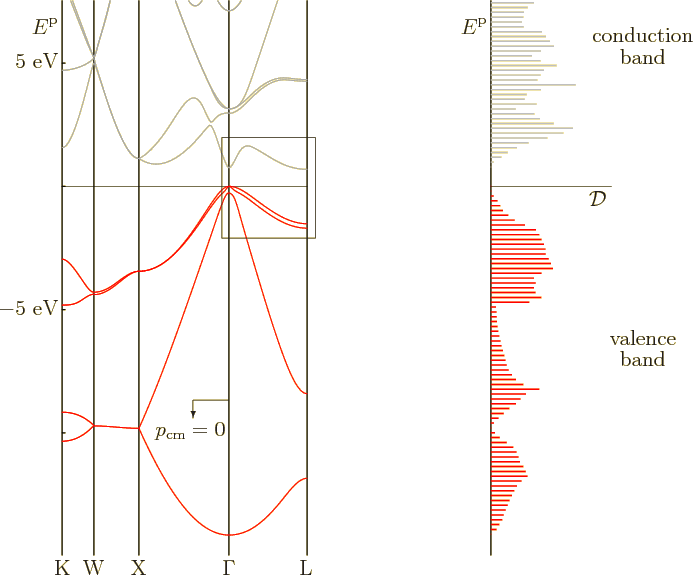$\begin{figure}\centering \setlength{\unitlength}{1pt} \begin{picture}(405,32... ...x(0,0){valence}} \put(170,110){\makebox(0,0){band}} \end{picture} \end{figure}$

Computed one-dimensional energy bands between the various points in the Brillouin zone can be found in the plot to the left in figure 6.30. The plot is for germanium. The zero level of energy was chosen as the top of the valence band. The various features of the plot agree well with other experimental and computational data.

The earlier spectrum for germanium in figure 6.26 showed only the part within the little frame in figure 6.30. That part is for the line between zero wave number and the point L in figure 6.29. Unlike figure 6.30, the earlier spectrum figure 6.26 showed both negative and positive wave numbers, as its left and right halves. On the other hand, the earlier spectrum showed only the highest one-dimensional valence band and the lowest one-dimensional conduction band. It was sufficient to show the top of the valence band and the bottom of the conduction band, but little else. As figure 6.30 shows, there are actually four different types of Bloch waves in the valence band. The energy range of each of the four is within the range of the combined valence band.

The complete valence band, as well as the lower part of the conduction band, is sketched in the spectrum to the right in figure 6.30. It shows the energy plotted against the density of states ${\cal D}$ . Note that the computed density of states for the conduction electrons is a mess when seen over its complete range. It is nowhere near parabolic as it would be for electrons in empty space, figure 6.1. Similarly the density of states applicable to the valence band holes is nowhere near an inverted parabola over its complete range. However, typically only about 1/40th of an eV below the top of the valence band and above the bottom of the conduction band is relevant for applications. That is very small on the scale of the figure.

An interesting feature of figure 6.30 is that two different energy bands merge at the top of the valence band. These two bands have the same energy at the top of the valence band, but very different curvature. And according to the earlier subsection 6.22.3, that means that they have different effective mass. Physicists therefore speak of light holes and heavy holes to keep the two types of quantum states apart. Typically even the heavy holes have effective masses less than the true electron mass, [29, pp. 214-216]. Diamond is an exception.

The spectrum of silicon is not that different from germanium. However, the bottom of the conduction band is now on the line from the origin $\Gamma$ to the point X in figure 6.29.