| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
Subsections
9.3 The Hartree-Fock Approximation
Many of the most important problems that you want to solve in quantum
mechanics are all about atoms and/or molecules. These problems
involve a number of electrons around a number of atomic nuclei.
Unfortunately, a full quantum solution of such a system of any
nontrivial size is very difficult. However, approximations can be
made, and as section 9.2 explained, the real skill you need
to master is solving the wave function for the electrons given the
positions of the nuclei.
But even given the positions of the nuclei, a brute-force solution for
any nontrivial number of electrons turns out to be prohibitively
laborious. The Hartree-Fock approximation is one of the most
important ways to tackle that problem, and has been so since the early
days of quantum mechanics. This section explains some of the ideas.
9.3.1 Wave function approximation
The key to the basic Hartree-Fock method is the assumptions it makes
about the form of the electron wave function. It will be assumed that
there are a total of  electrons in orbit around a number of nuclei.
The wave function describing the set of electrons then has the general
form:
electrons in orbit around a number of nuclei.
The wave function describing the set of electrons then has the general
form:
where  is the position of the electron numbered
is the position of the electron numbered  , and
, and
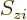 its spin (i.e. internal angular momentum) in a chosen
its spin (i.e. internal angular momentum) in a chosen
 -direction. Recall that while the position of an electron can
be anywhere in three-dimensional space, its spin component
-direction. Recall that while the position of an electron can
be anywhere in three-dimensional space, its spin component 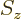 can have
only two measurable values:
can have
only two measurable values:  or
or 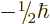 .
Because of the factor
.
Because of the factor  , an electron is a “particle of
spin one-half”. Such a particle is also called a “spin
doublet” because of the two possible spin values.
, an electron is a “particle of
spin one-half”. Such a particle is also called a “spin
doublet” because of the two possible spin values.
The square magnitude of the wave function above gives the probability
for the electrons 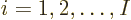 to be near the position
to be near the position  ,
per unit volume, with spin component
,
per unit volume, with spin component 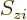 .
.
Of course, what the wave function is will also depend on where the
nuclei are. However, in this section, the nuclei are supposed to be
at given positions. Therefore to reduce the clutter, the dependence
of the electron wave function on the nuclear positions will not be
shown explicitly.
Hartree-Fock approximates the wave function above in terms of
single-electron wave functions. Each single-electron wave
function takes the form of a product of a spatial function  of the electron position
of the electron position  , times a function of the electron spin
component
, times a function of the electron spin
component 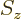 . The spin function is either taken to be
. The spin function is either taken to be  or
or
 ; by definition, function
; by definition, function 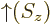 equals 1 if the spin
equals 1 if the spin 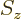 is
is  , and 0 if it is
, and 0 if it is 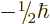 . Conversely,
function
. Conversely,
function  equals 0 if
equals 0 if 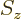 is
is  and 1 if it
is
and 1 if it
is 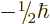 . Function
. Function  is called
is called spin-up
and 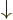
spin-down.
A complete single-electron wave function is then of the form
where 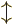 is either
is either  or
or 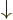 . Such a single-electron wave
function is called an “orbital” or more accurately a “spin orbital.” The reason is that people tend to think of the
single-electron wave function as describing a single electron being in
a particular orbit around the nuclei with a particular spin. Wrong,
of course: the electrons do not have well-defined positions on these
scales, so you cannot talk about
. Such a single-electron wave
function is called an “orbital” or more accurately a “spin orbital.” The reason is that people tend to think of the
single-electron wave function as describing a single electron being in
a particular orbit around the nuclei with a particular spin. Wrong,
of course: the electrons do not have well-defined positions on these
scales, so you cannot talk about orbits
But people do
tend to think of the spatial orbitals
 that way anyway.
that way anyway.
For simplicity, it will be assumed that the spin orbitals are taken to
be normalized;
if you integrate the square magnitude
of 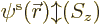 over all possible positions
over all possible positions  of the electron
and sum over the two possible values of its spin
of the electron
and sum over the two possible values of its spin 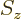 , you get 1.
Physically that merely expresses that the electron must be at
some position and have some spin for certain
(probability 1). The integral plus sum combination can be expressed
using the concise bra[c]ket notation from chapter 2;
, you get 1.
Physically that merely expresses that the electron must be at
some position and have some spin for certain
(probability 1). The integral plus sum combination can be expressed
using the concise bra[c]ket notation from chapter 2;
Such a bracket, or inner product,
is equivalent to a
dot product for functions.
If there is more than one electron, as will be assumed in this
section, a single spin orbital 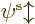 is not enough to create a
valid wave function for the complete system. In fact, the “Pauli exclusion principle” says that each of the
is not enough to create a
valid wave function for the complete system. In fact, the “Pauli exclusion principle” says that each of the  electrons
must go into a different spin orbital, chapter 5.7. So
a series of orbitals is needed,
electrons
must go into a different spin orbital, chapter 5.7. So
a series of orbitals is needed,
where the number of orbitals 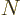 must be at least as big as the number
of electrons
must be at least as big as the number
of electrons  .
.
It will be assumed that any two different spin orbitals 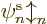 and
and 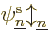 are taken to be
are taken to be orthogonal;
by
definition this means that their bracket is zero:
In short, it is assumed that the set of spin orbitals is orthonormal;
mutually orthogonal and normalized.
Note that the bracket above can be written as a product of a spatial
bracket and a spin one:
So for different spin orbitals to be orthogonal, either the spatial
states or the spin states must orthogonal; they do not both need to be
orthogonal. (To verify the expression above, just write the first
bracket out in terms of a spatial integral over  and a sum over
the two values of
and a sum over
the two values of 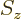 and reorder terms.)
and reorder terms.)
Note also that the spin states  and
and  are an orthonormal set:
are an orthonormal set:
So if the spin states are opposite, the spatial states do not need to
be orthogonal. In fact, the spatial states can then be the same.
The base Hartree-Fock method uses the absolute minimum number of
orbitals 

 . In that case, the simplest you could do to
create a system wave function is to put electron 1 in orbital 1,
electron 2 in orbital 2, etcetera. That would give the system wave
function
. In that case, the simplest you could do to
create a system wave function is to put electron 1 in orbital 1,
electron 2 in orbital 2, etcetera. That would give the system wave
function
A product of single-electron wave functions like this is called a
“Hartree product.”
But a single Hartree product like the one above is physically not
acceptable as a wave function. The Pauli exclusion principle is only
part of what is needed, chapter 5.7. The full
requirement is that a system wave function must be
antisymmetric under electron exchange:
the wave
function must simply change sign when any two electrons are swapped.
But if, say, electrons 1 and 2 are swapped in the Hartree product
above, it produces the new Hartree product
That is a fundamentally different wave function, not just minus the
first Hartree product; orbitals  and
and  are not
allowed to be equivalent.
are not
allowed to be equivalent.
To get a wave function that does simply change sign when electrons 1
and 2 are swapped, you can take the first Hartree product minus the
second one. That solves that problem. But it is not enough: the wave
function must also simply change sign if electrons 1 and 3 are
swapped. Or if 2 and 3 are swapped, etcetera.
So you must add more Hartree products with swapped electrons to the
mix. A lot more in fact. There are 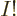 ways to order
ways to order  electrons,
and each ordering adds one Hartree product to the mix. (The Hartree
product gets a plus sign or a minus sign in the mix depending on
whether the number of swaps to get there from the first one is even or
odd). So for, say, a single carbon atom with
electrons,
and each ordering adds one Hartree product to the mix. (The Hartree
product gets a plus sign or a minus sign in the mix depending on
whether the number of swaps to get there from the first one is even or
odd). So for, say, a single carbon atom with 
 6 electrons,
writing down the full Hartree-Fock wave function would mean writing
down
6 electrons,
writing down the full Hartree-Fock wave function would mean writing
down 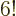
 720 Hartree products. Roughly a thousand of them, in
short. Of course, writing all that out would be insane. Fortunately,
there is a more concise way to write the complete wave function; it
uses a so-called
720 Hartree products. Roughly a thousand of them, in
short. Of course, writing all that out would be insane. Fortunately,
there is a more concise way to write the complete wave function; it
uses a so-called Slater determinant,
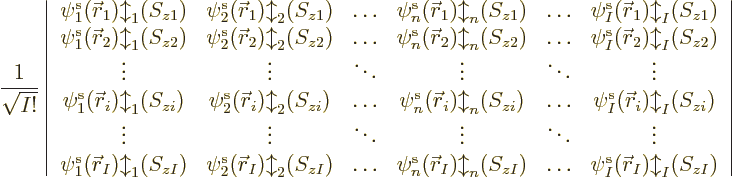 |
(9.15) |
The determinant multiplies out to the 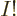 individual Hartree
products. (See chapter 5.7 and the notations section
for more on determinants.) The factor 1
individual Hartree
products. (See chapter 5.7 and the notations section
for more on determinants.) The factor 1
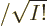 is there to
ensure that the wave function remains normalized after summing the
is there to
ensure that the wave function remains normalized after summing the
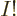 Hartree products together.
Hartree products together.
The most general system wave function  using only
using only 

 orbitals is any coefficient
orbitals is any coefficient  of magnitude 1 times the above Slater
determinant. However, displaying the Slater determinant fully as
above is still a lot to write and read. Therefore, from now on the
Slater determinant will be abbreviated as in
of magnitude 1 times the above Slater
determinant. However, displaying the Slater determinant fully as
above is still a lot to write and read. Therefore, from now on the
Slater determinant will be abbreviated as in
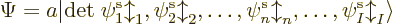 |
(9.16) |
where 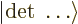 is the Slater determinant.
is the Slater determinant.
It is important to realize that using the minimum number of
single-electron functions will unavoidably produce an error that is
mathematically speaking not small {N.16}. To get a
vanishingly small error, you would need a large number of different
Slater determinants, not just one. Still, the results you get with the
basic Hartree-Fock approach may be good enough to satisfy your needs.
Or you may be able to improve upon them enough with
post-Hartree-Fock methods.
But none of that would be likely if you just selected the
single-electron functions  ,
,  , ...at random.
The cleverness in the Hartree-Fock approach will be in writing down
equations for these single-electron wave functions that produce the
best approximation possible with a single Slater determinant.
, ...at random.
The cleverness in the Hartree-Fock approach will be in writing down
equations for these single-electron wave functions that produce the
best approximation possible with a single Slater determinant.
Recall the approximate solutions that were written down for the
electrons in atoms in chapter 5.9. These solutions were
really single Slater determinants. To improve on these results, you
might think of trying to find more accurate ways to average out the
effects of the neighboring electrons than just putting them in the
nucleus as that chapter essentially did. You could smear them out
over some optimal area, say. But even if you did that, the
Hartree-Fock solution will still be better, because it gives the best
possible approximation obtainable with any single determinant.
That assumes of course that the spins are taken the same way.
Consider that problem for a second. Typically, a nonrelativistic
approach is used, in which spin effects on the energy are ignored.
Then spin only affects the antisymmetrization requirements.
Things are straightforward if you try to solve, say, a helium atom.
The correct ground state takes the form
The factor 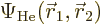 is the spatial wave function
that has the absolutely lowest energy, regardless of any
antisymmetrization concerns. This wave function must be symmetric
(unchanged) under electron exchange since the two electrons are
identical and the ground state is unique. The antisymmetrization
requirement is met because the spins combine together as shown in the
second factor above; this factor changes sign when the electrons are
exchanged. So the spatial state does not have to change sign.
is the spatial wave function
that has the absolutely lowest energy, regardless of any
antisymmetrization concerns. This wave function must be symmetric
(unchanged) under electron exchange since the two electrons are
identical and the ground state is unique. The antisymmetrization
requirement is met because the spins combine together as shown in the
second factor above; this factor changes sign when the electrons are
exchanged. So the spatial state does not have to change sign.
The combined spin state shown in the second factor above is called the
singlet state,
chapter 5.5.6. In the
singlet state the two spins cancel each other completely: the
net electron spin is zero. If you measure the net spin component in
any direction, not just the chosen  -direction, you get zero.
-direction, you get zero.
Based on the exact helium ground state wave function above, you would
take the Hartree-Fock approximation to be of the form
and then you would make things easier for yourself by postulating a
priori that the spatial orbitals are the same, 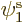

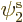 . Lo and behold, when you multiply out the Slater
determinant,
. Lo and behold, when you multiply out the Slater
determinant,
you get
This automagically reproduces the correct singlet spin state! (The
approximation comes in because the exact spatial ground state,
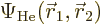 is not just the product of two
single-electron functions as in Hartree-Fock.) And you only need to
find one spatial orbital instead of two.
is not just the product of two
single-electron functions as in Hartree-Fock.) And you only need to
find one spatial orbital instead of two.
As discussed in chapter 5.9, a beryllium atom has two
electrons with opposite spins in the 1s
shell like
helium, and two more in the 2s
shell. An appropriate
Hartree-Fock wave function would be
in other words, two pairs of orbitals with the same spatial states and
opposite spins. Similarly, Neon has an additional 6 paired electrons
in a closed 2p
shell, and you could use 3 more pairs
of orbitals with the same spatial states and opposite spins. The
number of spatial orbitals that must be found in such solutions is
only half the number of electrons. This procedure is called the
“closed shell Restricted Hartree-Fock (RHF)” method. It
restricts the form of the spatial states to be pair-wise equal.
But now look at lithium. Lithium has two paired 1s electrons like
helium, and an unpaired 2s electron. For the third orbital in the
Hartree-Fock determinant, you will now have to make a choice: whether
to take it of the form  or
or  . Lets assume you
take
. Lets assume you
take  , so the wave function is
, so the wave function is
You have introduced a bias in the determinant: there is now a real
difference between the spatial orbitals 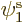 and
and 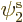 :
:
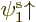 has the same spin as the third spin orbital, but
has the same spin as the third spin orbital, but
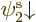 the opposite.
the opposite.
If you find the best approximation to the energy among all
possible spatial orbitals 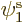 ,
, 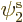 , and
, and 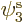 , you
will end up with orbitals
, you
will end up with orbitals 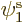 and
and 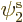 that are not the
same. Allowing for them to be different is called the “Unrestricted Hartree-Fock (UHF)” method. In general, you no
longer require that equivalent spatial orbitals are the same in their
spin-up and spin down versions. For a bigger system, you will end up
with one set of orthonormal spatial orbitals for the spin-up orbitals
and a different set of orthonormal spatial orbitals for the spin-down
ones. These two sets of orthonormal spatial orbitals are not
mutually orthogonal; the only reason the complete spin orbitals
are still orthonormal is because the two spins are orthogonal,
that are not the
same. Allowing for them to be different is called the “Unrestricted Hartree-Fock (UHF)” method. In general, you no
longer require that equivalent spatial orbitals are the same in their
spin-up and spin down versions. For a bigger system, you will end up
with one set of orthonormal spatial orbitals for the spin-up orbitals
and a different set of orthonormal spatial orbitals for the spin-down
ones. These two sets of orthonormal spatial orbitals are not
mutually orthogonal; the only reason the complete spin orbitals
are still orthonormal is because the two spins are orthogonal,
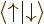
 0.
0.
If instead of using unrestricted Hartree-Fock, you insist on demanding
that the spatial orbitals for spin up and down do form a single set of
orthonormal functions, it is called “open shell Restricted Hartree-Fock (RHF).” In the case of
lithium, you would then demand that 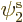 equals
equals 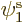 .
Since the best (in terms of energy) solution has them different, your
solution is then no longer the best possible. You pay a price, but
you now only need to find two spatial orbitals rather than three. The
spin orbital
.
Since the best (in terms of energy) solution has them different, your
solution is then no longer the best possible. You pay a price, but
you now only need to find two spatial orbitals rather than three. The
spin orbital  without a matching opposite-spin orbital
counts as an open shell. For nitrogen, you might want to use three
open shells to represent the three different spatial states 2p
without a matching opposite-spin orbital
counts as an open shell. For nitrogen, you might want to use three
open shells to represent the three different spatial states 2p ,
2p
,
2p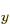 , and 2p
, and 2p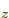 with an unpaired electron in it.
with an unpaired electron in it.
If you use unrestricted Hartree-Fock instead, you will need to compute
more spatial functions, and you pay another price, spin. Since all
spin effects in the Hamiltonian are ignored, it commutes with the spin
operators. So, the exact energy eigenfunctions are also, or can be
taken to be also, spin eigenfunctions. Restricted Hartree-Fock has
the capability of producing approximate energy eigenstates with well
defined spin. Indeed, as you saw for helium, in restricted
Hartree-Fock all the paired spin-up and spin-down states combine into
zero-spin singlet states. If any additional unpaired states are all
spin up, say, you get an energy eigenstate with a net spin equal to
the sum of the spins of the unpaired states. This allows you to deal
with typical atoms, including lithium and nitrogen, very nicely.
But a true unrestricted Hartree-Fock solution does not have correct,
definite, spin. For two electrons to produce states of definite
combined spin, the coefficients of spin-up and spin-down must come in
specific ratios. As a simple example, an unrestricted Slater
determinant of 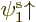 and
and 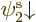 with unequal spatial
orbitals multiplies out to
with unequal spatial
orbitals multiplies out to
or, writing the spin combinations in terms of singlets (which change
sign under electron exchange) and triplets (which do not),
So the spin will be some combination of the singlet state, the first
term, and a triplet state, the second. And the precise combination
will depend on the spatial locations of the electrons to boot. Now
while the singlet state has net spin 0, triplet states have net spin
1. So the net spin is uncertain, either 0 or 1, even though it should
not be. (Spin 1 implies that the measured component of the spin in any
direction must be one of the triplet of values  , 0, or
, 0, or
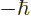 . For the particular triplet state shown above, the component
of spin in the
. For the particular triplet state shown above, the component
of spin in the  -direction happens to be zero. But the net spin is
not; in a direction normal to the
-direction happens to be zero. But the net spin is
not; in a direction normal to the  -direction, the spin will be
measured to be either
-direction, the spin will be
measured to be either  or
or 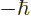 .) However, despite the spin
problem, it may be noted that unrestricted wave functions are commonly
used as first approximations of doublet (spin
.) However, despite the spin
problem, it may be noted that unrestricted wave functions are commonly
used as first approximations of doublet (spin  ) and triplet
(spin 1) states anyway [46, p. 105].
) and triplet
(spin 1) states anyway [46, p. 105].
To show that all this can make a real difference, take the example of
the hydrogen molecule, chapter 5.2, when the two nuclei are
far apart. The correct electronic ground state is
where 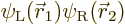 is the state in which
electron 1 is around the left proton and electron 2 around the right
one, and
is the state in which
electron 1 is around the left proton and electron 2 around the right
one, and 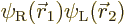 is the same state
but with the electrons reversed. Note that, like for the helium atom,
the spatial state is symmetric under electron exchange. However, it
is not just a product of two single-electron functions but a sum of
two of such products. Note also that the correct spin state is the
singlet one with zero net spin, just like for the helium atom. It
takes care of the antisymmetrization requirement.
is the same state
but with the electrons reversed. Note that, like for the helium atom,
the spatial state is symmetric under electron exchange. However, it
is not just a product of two single-electron functions but a sum of
two of such products. Note also that the correct spin state is the
singlet one with zero net spin, just like for the helium atom. It
takes care of the antisymmetrization requirement.
Now try to approximate this solution with a restricted closed shell
Hartree-Fock wave function of the form
Multiplying out the determinant gives
Note that you do get the correct singlet spin state. But 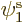 will be something like
will be something like 

 ;
the energy of either electron is lowest when it is near one of the
nuclei. If you multiply out the resulting spatial wave function, the
terms include
;
the energy of either electron is lowest when it is near one of the
nuclei. If you multiply out the resulting spatial wave function, the
terms include  and
and
 , in addition to the correct
, in addition to the correct
 and
and  . That
produces a 50/50 chance that the two electrons are found around the
same nucleus. That is all wrong, since the electrons repel
each other: if one electron is around the left nucleus, the other
electron should be around the right nucleus. The computed energy,
which should be that of two neutral hydrogen atoms far apart, will be
much too high due to electron-electron repulsion.
. That
produces a 50/50 chance that the two electrons are found around the
same nucleus. That is all wrong, since the electrons repel
each other: if one electron is around the left nucleus, the other
electron should be around the right nucleus. The computed energy,
which should be that of two neutral hydrogen atoms far apart, will be
much too high due to electron-electron repulsion.
(Fortunately, at the nuclear separation distance corresponding to the
ground state of the complete molecule, the errors are much less,
[46, p. 166]. Note that if you put the two nuclei
completely on top of each other, you get a helium atom, for which
Hartree-Fock gives a much more reasonable electron energy. Only when
you are breaking the bond,
dissociating the molecule,
i.e. taking the nuclei far apart, do you get into major trouble.)
If instead you would use unrestricted Hartree-Fock, say
you should find 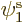

 and
and 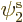

 (or vice versa), which would produce a wave function
(or vice versa), which would produce a wave function
In both terms, if the first electron is around the one nucleus, the
second electron is around the other. So this produces the correct
energy, that of two neutral hydrogen atoms. But the spin is now all
wrong. It is not a singlet state, but the combination of a singlet
and a triplet state already written down earlier. Little in life is
ideal, is it?
(Actually there is a dirty trick to fix this. Note that which of the
two orbitals you give spin-up and which spin-down is physically
immaterial. So there is a trivially different solution
If you take a 50/50 combination of the original Slater determinant and
minus the one above, you get the correct singlet spin state. And the
spatial state will now be the correct average of
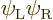 and
and  to boot.
This spatial state is more accurate than just two neutral atoms if the
distance between the nuclei decreases, chapter 5.2. All
this for free! This sort of dirty trick in Hartree-Fock is called a
“spin adapted configuration.” It is usually used to deal with a
few open shells in an otherwise closed-shell restricted Hartree-Fock
configuration.)
to boot.
This spatial state is more accurate than just two neutral atoms if the
distance between the nuclei decreases, chapter 5.2. All
this for free! This sort of dirty trick in Hartree-Fock is called a
“spin adapted configuration.” It is usually used to deal with a
few open shells in an otherwise closed-shell restricted Hartree-Fock
configuration.)
All of the above may be much more than you ever wanted to hear about
the wave function. The purpose was mainly to indicate that things are
not as simple as you might initially suppose. As the examples showed,
some understanding of the system that you are trying to model
definitely helps. Or experiment with different approaches.
Let’s go on to the next step: how to get the equations for the
spatial orbitals  that give the most
accurate approximation of a multi-electron problem. The expectation
value of energy will be needed for that, and to get that, first the
Hamiltonian is needed. That will be the subject of the next
subsection.
that give the most
accurate approximation of a multi-electron problem. The expectation
value of energy will be needed for that, and to get that, first the
Hamiltonian is needed. That will be the subject of the next
subsection.
9.3.2 The Hamiltonian
The nonrelativistic Hamiltonian of the system of  electrons
consists of a number of contributions. First there is the kinetic
energy of the electrons; the sum of the kinetic energy operators of
the individual electrons:
electrons
consists of a number of contributions. First there is the kinetic
energy of the electrons; the sum of the kinetic energy operators of
the individual electrons:
 |
(9.17) |
Next there is the potential energy due to the ambient electric field
that the electrons move in. It will be assumed that this field is
caused by 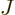 nuclei, numbered using an index
nuclei, numbered using an index  , and having
charge
, and having
charge 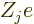 (i.e. there are
(i.e. there are 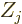 protons in nucleus number
protons in nucleus number  ).
In that case, the total potential energy due to nucleus-electron
attractions is, summing over all electrons and over all nuclei:
).
In that case, the total potential energy due to nucleus-electron
attractions is, summing over all electrons and over all nuclei:
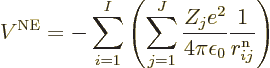 |
(9.18) |
where 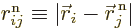 is the distance
between electron number
is the distance
between electron number  and nucleus number
and nucleus number  , and
, and 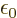
 8.85 10
8.85 10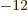 C
C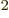 /J m is the permittivity of space.
/J m is the permittivity of space.
And now for the black plague of quantum mechanics, the electron to
electron repulsions. The potential energy for those repulsions is
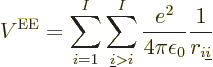 |
(9.19) |
where  is the distance between electron
number
is the distance between electron
number  and electron number
and electron number 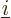 . To avoid counting each
repulsion energy twice, (the second time with reversed electron
order), the second electron number is required to be larger than the
first.
. To avoid counting each
repulsion energy twice, (the second time with reversed electron
order), the second electron number is required to be larger than the
first.
Without this repulsion between different electrons, you could solve
for each electron separately, and all would be nice. But you do have
it, and so you really need to solve for all electrons at once, usually
an impossible task. You may recall that when chapter 5.9
examined the atoms heavier than hydrogen, those with more than one
electron, the discussion cleverly threw out the electron to electron
repulsion terms, by assuming that the effect of each neighboring
electron is approximately like canceling out one proton in the
nucleus. And you may also remember how this outrageous assumption led
to all those wrong predictions that had to be corrected by various
excuses. The Hartree-Fock approximation tries to do better than that.
It is helpful to split the Hamiltonian into the single electron terms
and the troublesome interactions, as follows,
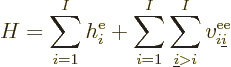 |
(9.20) |
where 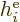 is the single-electron Hamiltonian of electron
is the single-electron Hamiltonian of electron
 ,
,
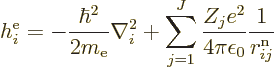 |
(9.21) |
and 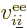 is the electron
is the electron  to electron
to electron 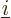 repulsion
potential energy,
repulsion
potential energy,
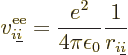 |
(9.22) |
Note that 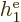 ,
, 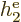 , ...,
, ..., 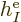 all take the same
general form; the difference is just in which electron you are talking
about. That is not surprising because the electrons all have the same
properties. Similarly, the difference between
all take the same
general form; the difference is just in which electron you are talking
about. That is not surprising because the electrons all have the same
properties. Similarly, the difference between 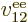 ,
,
 , ...,
, ..., 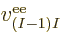 is just in which pair of
electrons you talk about.
is just in which pair of
electrons you talk about.
9.3.3 The expectation value of energy
As was discussed in more detail in section 9.1, to find
the best possible Hartree-Fock approximation, the expectation value of
energy will be needed. For example, the best approximation to the
ground state is the one that has the smallest expectation value of
energy.
The expectation value of energy  is defined as the inner
product
is defined as the inner
product
where 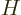 is the Hamiltonian as given in the previous subsection.
There is a problem with using this expression mindlessly, though.
Take once again the example of the arsenic atom. There are 33
electrons in this atom, so you could try to choose 33 promising
single-electron wave functions to describe it. You could then try to
multiply out the Slater determinant for
is the Hamiltonian as given in the previous subsection.
There is a problem with using this expression mindlessly, though.
Take once again the example of the arsenic atom. There are 33
electrons in this atom, so you could try to choose 33 promising
single-electron wave functions to describe it. You could then try to
multiply out the Slater determinant for  , but that produces
33!, or about 4 10
, but that produces
33!, or about 4 10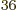 , Hartree products. If you put these 33!
terms in both sides of the inner product, you get (33!)
, Hartree products. If you put these 33!
terms in both sides of the inner product, you get (33!)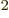 or
7.5 10
or
7.5 10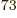 pairs of terms, each producing one inner product that must
be integrated. Now since there are 3 coordinates for each of the
positions of the 33 electrons, this means that each term requires
integration over 99 scalar coordinates. Even using only 10 points in
each direction, that would mean evaluating 10
pairs of terms, each producing one inner product that must
be integrated. Now since there are 3 coordinates for each of the
positions of the 33 electrons, this means that each term requires
integration over 99 scalar coordinates. Even using only 10 points in
each direction, that would mean evaluating 10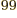 integration
points for each of the 7.5 10
integration
points for each of the 7.5 10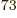 pairs of terms. A computer that
could do that is unimaginable. As of 2014, the fastest computer in
the world can do no more than 10
pairs of terms. A computer that
could do that is unimaginable. As of 2014, the fastest computer in
the world can do no more than 10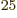 floating point computations
if it stays at it for 10 years.
floating point computations
if it stays at it for 10 years.
Fortunately, it turns out, {D.52}, that almost all
of those integrations are trivial since the single-electron functions
are orthonormal. If you sit down and identify what is really left,
you find that only a few three-dimensional and six-dimensional inner products
survive the weeding-out process.
In particular, the single-electron Hamiltonians from the previous
subsection produce only single-electron energy expectation values of
the general form
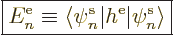 |
(9.23) |
If you had only one single electron, and it was in the spatial
single-particle state 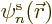 , the above inner product would
be its energy.
, the above inner product would
be its energy.
The combined single-electron energy for all  electrons is then
electrons is then
It is just as if you had electron 1 in state 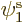 , electron 2 in
state
, electron 2 in
state 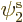 , etcetera. Of course, that is not really true.
Antisymmetrization requires that all electrons are partly in all
states. Indeed, if you look a bit closer at the math, you see that
each of the
, etcetera. Of course, that is not really true.
Antisymmetrization requires that all electrons are partly in all
states. Indeed, if you look a bit closer at the math, you see that
each of the  electrons contributes an equal fraction 1
electrons contributes an equal fraction 1
 to
each of the
to
each of the  terms above. But it does not make a real difference.
Without electron-electron interactions, quantum mechanics would be so
much easier!
terms above. But it does not make a real difference.
Without electron-electron interactions, quantum mechanics would be so
much easier!
But the repulsions are there. The Hamiltonians of the repulsions turn
out to produce six-dimensional spatial inner products of two types. The
inner products of the first type are called “Coulomb integrals:”
 |
(9.24) |
To understand the Coulomb integrals better, the inner product above
can be written out explicitly as an integral, while also expanding
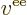 :
:
The integrand equals the probability of an electron in state
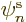 to be found near a position
to be found near a position  , times the probability
of an electron in state
, times the probability
of an electron in state 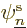 to be found near a position
to be found near a position
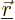 , times the Coulomb repulsion energy if the two electrons are at
those positions. In short,
, times the Coulomb repulsion energy if the two electrons are at
those positions. In short,  is the expectation value of the
Coulomb repulsion potential between an electron in state
is the expectation value of the
Coulomb repulsion potential between an electron in state 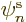 and one in state
and one in state 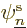 . Thinking again of electron 1 in state
. Thinking again of electron 1 in state
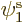 , electron 2 in state
, electron 2 in state 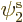 , etcetera, the total
Coulomb repulsion energy would be
, etcetera, the total
Coulomb repulsion energy would be
which is indeed the correct combined sum of the Coulomb integrals.
Unfortunately, that is not the complete story for the repulsion
energy. Recall that there are 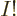 different ways in which you can
distribute the
different ways in which you can
distribute the  electrons over the
electrons over the  single particle states. And
the antisymmetrization requirement requires that the system wave
function is an equal combination of all these
single particle states. And
the antisymmetrization requirement requires that the system wave
function is an equal combination of all these 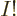 different
possibilities. In terms of classical physics, it might still seem
that this should make no difference: if any one of these
different
possibilities. In terms of classical physics, it might still seem
that this should make no difference: if any one of these 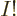 possibilities is true, then the others must be untrue. But quantum
mechanics allows states in which the electrons are distributed in one
way to interact with states in which they are distributed in another
way. That produces the so-called “exchange integrals:”
possibilities is true, then the others must be untrue. But quantum
mechanics allows states in which the electrons are distributed in one
way to interact with states in which they are distributed in another
way. That produces the so-called “exchange integrals:”
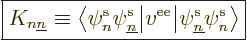 |
(9.25) |
Written out explicitly, that equals
It is an interaction of the possibility that the first electron is in
state 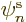 and the second in state
and the second in state 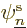 with the
possibility that the second electron is in state
with the
possibility that the second electron is in state 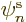 and the
first in state
and the
first in state 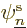 . This book likes to call terms like this
. This book likes to call terms like this
twilight terms,
since in terms of classical physics
they do not make sense.
It may be noted that a single Hartree product satisfying the Pauli
exclusion principle would not produce exchange integrals; in such a
wave function, there is no possibility for an electron to be in
another state. But don't start thinking that the exchange integrals
are there just because the wave function must be antisymmetric under
electron exchange. They, and others, would show up in any reasonably
general wave function. You can think of the exchange integrals
instead as Coulomb integrals with the electrons in the right hand side
of the inner product exchanged.
Adding it all up, the expectation energy of the complete system of  electrons can be written as
electrons can be written as
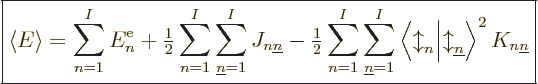 |
(9.26) |
Note that the above expression sums over all values of 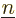 , not just
, not just
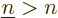 . That counts each pair of single-electron wave functions
twice, so factors one-half have been added to compensate. It also
adds terms in which
. That counts each pair of single-electron wave functions
twice, so factors one-half have been added to compensate. It also
adds terms in which  , both electrons in the same state, which
is not allowed by the Pauli principle. But since
, both electrons in the same state, which
is not allowed by the Pauli principle. But since 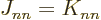 ,
these additional terms cancel each other.
,
these additional terms cancel each other.
Note also the spin inner products multiplying the exchange terms.
These are zero if the two states have opposite spin, so there are no
exchange contributions between electrons in spin orbitals of opposite
spins. And if the spin orbitals have the same spin, the spin inner
product is 1, so the square is somewhat superfluous.
There are also some a priori things you can say about the Coulomb and
exchange integrals, {D.53}; they are real, and
additionally
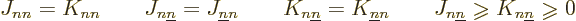 |
(9.27) |
Note in particular that since the  terms are positive, they
lower the net expectation energy of the system. So a wave function
consisting of a single Hartree product, which produces no exchange
terms, cannot be the state of lowest energy. Even without the
antisymmetrization requirement, you would need Hartree products with
the electrons exchanged, simply to lower the energy.
terms are positive, they
lower the net expectation energy of the system. So a wave function
consisting of a single Hartree product, which produces no exchange
terms, cannot be the state of lowest energy. Even without the
antisymmetrization requirement, you would need Hartree products with
the electrons exchanged, simply to lower the energy.
It is actually somewhat tricky to prove that the  terms are
positive and so lower the energy, {D.53}. But there
is a simple physical reason why you might guess that an
antisymmetric wave function would lower the electron-electron
repulsion energy compared to the individual Hartree products from
which it is made up. In particular, the Coulomb repulsion between
electrons becomes very large when they get close together. But for an
anti-symmetric wave function, unlike for a single Hartree product, the
relative probability of electrons of the same spin getting close
together is vanishingly small. That prevents any strong Coulomb
repulsion between electrons of the same spin.
terms are
positive and so lower the energy, {D.53}. But there
is a simple physical reason why you might guess that an
antisymmetric wave function would lower the electron-electron
repulsion energy compared to the individual Hartree products from
which it is made up. In particular, the Coulomb repulsion between
electrons becomes very large when they get close together. But for an
anti-symmetric wave function, unlike for a single Hartree product, the
relative probability of electrons of the same spin getting close
together is vanishingly small. That prevents any strong Coulomb
repulsion between electrons of the same spin.
(Recall that the relative probability for electrons to be at given
positions and spins is given by the square magnitude of the wave
function at those positions and spins. Now an antisymmetric wave
function must be zero wherever any two electrons are at the same
position with the same spin, making this impossible. After all, if
you swap the two electrons, the antisymmetric wave function must
change sign. But since neither electron changes position nor spin,
the wave function cannot change either. Something can only change
sign and stay the same if it is zero. See also
{A.34}.)
The analysis given in this subsection can easily be extended to
generalized orbitals that take the form
However, the normal unrestricted spin-up or spin-down orbitals, in
which either 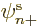 or
or  is zero, already satisfy
the variational requirement
is zero, already satisfy
the variational requirement 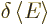
 0 even if generalized
variations in the orbitals are allowed, {N.17}.
0 even if generalized
variations in the orbitals are allowed, {N.17}.
In any case, the expectation value of energy has been found.
9.3.4 The canonical Hartree-Fock equations
The previous subsection found the expectation value of energy for any
electron wave function described by a single Slater determinant. The
final step is to find the orbitals that produce the best approximation
of the true wave function using such a single determinant. For the
ground state, the best single determinant would be the one with the
lowest expectation value of energy. But surely you would not want to
guess spatial orbitals at random until you find some with really,
really, low energy.
What you would like to have is specific equations for the best spatial
orbitals that you can then solve in a methodical way. And you can
have them using the methods of section 9.1,
{D.54}. In unrestricted Hartree-Fock, for every spatial
orbital 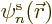 there is an equation of the form:
there is an equation of the form:
![\begin{displaymath}
\fbox{$\displaystyle
\begin{array}[b]{l}
\displaystyle
h...
... r}///
= \epsilon_n \pe n/{\skew0\vec r}///
\end{array} $} %
\end{displaymath}](img2098.gif) |
(9.28) |
These are called the canonical Hartree-Fock equations.
For equations valid for the restricted closed-shell and
single-determinant open-shell approximations, see the derivation in
{D.54}.
Recall that 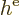 is the single-electron Hamiltonian consisting of the
electron's kinetic energy and potential energy due to nuclear
attractions, and that
is the single-electron Hamiltonian consisting of the
electron's kinetic energy and potential energy due to nuclear
attractions, and that 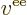 is the potential energy of repulsion
between the electron and another at a position
is the potential energy of repulsion
between the electron and another at a position 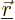 :
:
So, if there were no electron-electron repulsions, i.e. 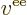
 0, the canonical equations above would be single-electron Hamiltonian
eigenvalue problems of the form
0, the canonical equations above would be single-electron Hamiltonian
eigenvalue problems of the form 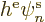

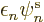 where
where 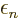 would be the energy of the
single-electron orbital. This is really what happened in the
approximate analysis of atoms in chapter 5.9: the electron
to electron repulsions were ignored there in favor of nuclear strength
reductions, and the result was single-electron hydrogen-atom orbitals.
would be the energy of the
single-electron orbital. This is really what happened in the
approximate analysis of atoms in chapter 5.9: the electron
to electron repulsions were ignored there in favor of nuclear strength
reductions, and the result was single-electron hydrogen-atom orbitals.
In the presence of electron to electron repulsions, the equations for
the orbitals can still symbolically be written as if they were
single-electron eigenvalue problems,
where 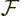 is called the “Fock operator,” and is written out further as:
is called the “Fock operator,” and is written out further as:
The first term in the Fock operator is the single-electron
Hamiltonian. The mischief is in the innocuous-looking second term
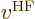 . Supposedly, this is the potential energy related
to the repulsion by the other electrons. What is it? Well, it will
have to be the terms in the canonical equations (9.28) not
described by the single-electron Hamiltonian
. Supposedly, this is the potential energy related
to the repulsion by the other electrons. What is it? Well, it will
have to be the terms in the canonical equations (9.28) not
described by the single-electron Hamiltonian 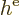 :
:
The definition of the Fock operator is unavoidably in terms of spin
rather than just spatial orbitals: the spin of the state on which it
operates must be known to evaluate the final term.
Note that the above expression did not give an expression for
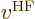 by itself, but only for
by itself, but only for 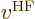 applied to an
arbitrary single-electron function
applied to an
arbitrary single-electron function 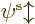 . The reason is that
. The reason is that
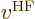 is not a normal potential at all: the second term, the
one due to the exchange integrals, does not multiply
is not a normal potential at all: the second term, the
one due to the exchange integrals, does not multiply 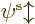 by a
potential function, it shoves it into an inner product! The
Hartree-Fock
by a
potential function, it shoves it into an inner product! The
Hartree-Fock potential
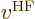 is an
operator, not a normal potential energy. Given a
single-electron function including spin, it produces another
single-electron function including spin.
is an
operator, not a normal potential energy. Given a
single-electron function including spin, it produces another
single-electron function including spin.
Actually, even that is not quite true. The Hartree-Fock
potential
is only an operator after you have
found the orbitals  ,
,  , ...,
, ..., 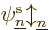 ,
...,
,
..., 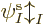 appearing in it. While you are still trying to
find them, the Fock
appearing in it. While you are still trying to
find them, the Fock operator
is not even an operator,
it is just a thing.
However, given the
orbitals, at least the Fock operator is a Hermitian one, one that can
be taken to the other side if it appears in an inner product, and that
has real eigenvalues and a complete set of eigenfunctions,
{D.55}.
So how do you solve the canonical Hartree-Fock equations for the
orbitals 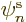 ? If the Hartree-Fock potential
? If the Hartree-Fock potential
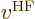 was a known operator, you would have only linear,
single-electron eigenvalue problems to solve. That would be
relatively easy, as far as those things come. But since the operator
was a known operator, you would have only linear,
single-electron eigenvalue problems to solve. That would be
relatively easy, as far as those things come. But since the operator
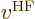 contains the unknown orbitals, you do not have a linear
problem at all; it is a system of coupled cubic equations in
infinitely many unknowns. The usual way to solve it is iteratively:
you guess an approximate form of the orbitals and plug it into the
Hartree-Fock potential. With this guessed potential, the orbitals may
then be found from solving linear eigenvalue problems. If all goes
well, the obtained orbitals, though not perfect, will at least be
better than the ones that you guessed at random. So plug those
improved orbitals into the Hartree-Fock potential and solve the
eigenvalue problems again. Still better orbitals should result. Keep
going until you get the correct solution to within acceptable
accuracy.
contains the unknown orbitals, you do not have a linear
problem at all; it is a system of coupled cubic equations in
infinitely many unknowns. The usual way to solve it is iteratively:
you guess an approximate form of the orbitals and plug it into the
Hartree-Fock potential. With this guessed potential, the orbitals may
then be found from solving linear eigenvalue problems. If all goes
well, the obtained orbitals, though not perfect, will at least be
better than the ones that you guessed at random. So plug those
improved orbitals into the Hartree-Fock potential and solve the
eigenvalue problems again. Still better orbitals should result. Keep
going until you get the correct solution to within acceptable
accuracy.
You will know when you have got the correct solution since the
Hartree-Fock potential will no longer change; the potential that you
used to compute the final set of orbitals is really the potential that
those final orbitals produce. In other words, the final Hartree-Fock
potential that you compute is consistent with the final orbitals.
Since the potential would be a field if it was not an operator, that
explains why such an iterative method to compute the Hartree-Fock
solution is called a “self-consistent field method.” It is like calling an iterative
scheme for the Laplace equation on a mesh a “self-consistent
neighbors method,” instead of point relaxation.
Surely the equivalent for Hartree-Fock, like “iterated
potential” or potential relaxation
would have
been much clearer to a general audience?
9.3.5 Additional points
This brief section was not by any means a tutorial of the Hartree-Fock
method. The purpose was only to explain the basic ideas in terms of
the notations and coverage of this book. If you actually want to
apply the method, you will need to take up a book written by experts
who know what they are talking about. The book by Szabo and Ostlund
[46] was the main reference for this section, and is
recommended as a well written introduction. Below are some additional
concepts you may want to be aware of.
9.3.5.1 Meaning of the orbital energies
In the single electron case, the orbital energy
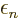 in the canonical Hartree-Fock equation
in the canonical Hartree-Fock equation
represents the actual energy of the electron. It also represents the
ionization energy, the energy required to take the electron away from
the nuclei and leave it far away at rest. This subsubsection will
show that in the multiple electron case, the “orbital
energies” 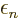 are not orbital energies in the sense of
giving the contributions of the orbitals to the total expectation
energy. However, they can still be taken to be approximate ionization
energies. This result is known as “Koopman’s theorem.”
are not orbital energies in the sense of
giving the contributions of the orbitals to the total expectation
energy. However, they can still be taken to be approximate ionization
energies. This result is known as “Koopman’s theorem.”
To verify the theorem, a suitable equation for 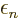 is needed.
It can be found by taking an inner product of the canonical equation
above with
is needed.
It can be found by taking an inner product of the canonical equation
above with 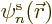 , i.e. by putting
, i.e. by putting 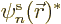 to
the left of both sides and integrating over
to
the left of both sides and integrating over  . That
produces
. That
produces
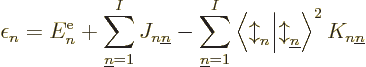 |
(9.29) |
which consists of the single-electron energy  , Coulomb
integrals
, Coulomb
integrals  and exchange integrals
and exchange integrals  as defined in
subsection 9.3.3. It can already be seen that if all the
as defined in
subsection 9.3.3. It can already be seen that if all the
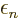 are summed together, it does not produce the total
expectation energy (9.26), because that one includes a factor
are summed together, it does not produce the total
expectation energy (9.26), because that one includes a factor
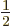 in front of the Coulomb and exchange integrals. So,
in front of the Coulomb and exchange integrals. So,
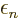 cannot be seen as the part of the system energy
associated with orbital
cannot be seen as the part of the system energy
associated with orbital 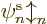 in any meaningful sense.
in any meaningful sense.
However, 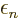 can still be viewed as an approximate ionization
energy. Assume that the electron is removed from orbital
can still be viewed as an approximate ionization
energy. Assume that the electron is removed from orbital
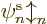 , leaving the electron at infinite distance at
rest. No, scratch that; all electrons share orbital
, leaving the electron at infinite distance at
rest. No, scratch that; all electrons share orbital
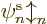 , not just one. Assume that one electron is
removed from the system and that the remaining
, not just one. Assume that one electron is
removed from the system and that the remaining  electrons stay
out of the orbital
electrons stay
out of the orbital 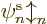 . Then, if it is assumed that the other orbitals do not change, the new
system’s Slater determinant is the same as the original
system’s, except that column
. Then, if it is assumed that the other orbitals do not change, the new
system’s Slater determinant is the same as the original
system’s, except that column  and a row have been removed. The
expectation energy of the new state then equals the original
expectation energy, except that
and a row have been removed. The
expectation energy of the new state then equals the original
expectation energy, except that  and the
and the  -th column
plus the
-th column
plus the  -th row of the Coulomb and exchange integral
matrices have been removed. The energy removed is then exactly
-th row of the Coulomb and exchange integral
matrices have been removed. The energy removed is then exactly
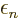 above. (While
above. (While 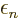 only involves the
only involves the
 -th row of the matrices, not the
-th row of the matrices, not the  -th column, it does
not have the factor
-th column, it does
not have the factor 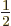 in front of them like the expectation
energy does. And rows equal columns in the matrices, so half the row
in
in front of them like the expectation
energy does. And rows equal columns in the matrices, so half the row
in 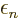 counts as the half column in the expectation energy
and the other half as the half row. This counts the element
counts as the half column in the expectation energy
and the other half as the half row. This counts the element 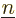

 twice, but that is zero anyway since
twice, but that is zero anyway since 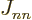

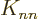 .)
.)
So by the removal of the electron from
(read: and)
orbital 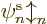 , an amount of energy
, an amount of energy 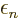 has been
removed from the expectation energy. Better put, a positive amount of
energy
has been
removed from the expectation energy. Better put, a positive amount of
energy 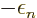 has been added to the expectation energy. So the
ionization energy is
has been added to the expectation energy. So the
ionization energy is 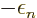 if the electron is removed from
orbital
if the electron is removed from
orbital 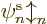 according to this story.
according to this story.
Of course, the assumption that the other orbitals do not change after
the removal of one electron and orbital is dubious. If you were a
lithium electron in the expansive 2s state, and someone removed one of
the two inner 1s electrons, would you not want to snuggle up a lot
more closely to the now much less shielded three-proton nucleus? On
the other hand, in the more likely case that someone removed the 2s
electron, it would probably not seem like that much of an event to the
remaining two 1s electrons near the nucleus, and the assumption that
the orbitals do not change would appear more reasonable. And
normally, when you say ionization energy, you are talking about
removing the electron from the highest energy state.
But still, you should really recompute the remaining two orbitals from
the canonical Hartree-Fock equations for a two-electron system to get
the best, lowest, energy for the new  electron ground state. The
energy you get by not doing so and just sticking with the original
orbitals will be too high. Which means that all else being the same,
the ionization energy will be too high too.
electron ground state. The
energy you get by not doing so and just sticking with the original
orbitals will be too high. Which means that all else being the same,
the ionization energy will be too high too.
However, there is another error of importance here, the error in the
Hartree-Fock approximation itself. If the original and final system
would have the same Hartree-Fock error, then it would not make a
difference and 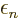 would overestimate the ionization energy
as described above. But Szabo and Ostlund
[46, p. 128] note that Hartree-Fock tends to
overestimate the energy for the original larger system more than for
the final smaller one. The difference in Hartree-Fock error tends to
compensate for the error you make by not recomputing the final
orbitals, and in general the orbital energies provide reasonable first
approximations to the experimental ionization energies.
would overestimate the ionization energy
as described above. But Szabo and Ostlund
[46, p. 128] note that Hartree-Fock tends to
overestimate the energy for the original larger system more than for
the final smaller one. The difference in Hartree-Fock error tends to
compensate for the error you make by not recomputing the final
orbitals, and in general the orbital energies provide reasonable first
approximations to the experimental ionization energies.
The opposite of ionization energy is “electron affinity,” the energy with which the atom or molecule
will bind an additional free electron [in its valence shell],
{N.19}. It is not to be confused with
electronegativity, which has to do with willingness to take on
electrons in chemical bonds, rather than free electrons.
To compute the electron affinity of an atom or molecule with  electrons using the Hartree-Fock method, you can either recompute the
electrons using the Hartree-Fock method, you can either recompute the
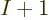 orbitals with the additional electron from scratch, or much
easier, just use the Fock operator of the
orbitals with the additional electron from scratch, or much
easier, just use the Fock operator of the  electrons to compute one
more orbital
electrons to compute one
more orbital 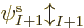 . In the later case however, the
energy of the final system will again be higher than Hartree-Fock, and
it being the larger system, the Hartree-Fock energy will be too high
compared to the
. In the later case however, the
energy of the final system will again be higher than Hartree-Fock, and
it being the larger system, the Hartree-Fock energy will be too high
compared to the  -electron system already. So now the errors
add up, instead of subtract as in the ionization case. If the final
energy is too high, then the computed binding energy will be too low,
so you would expect
-electron system already. So now the errors
add up, instead of subtract as in the ionization case. If the final
energy is too high, then the computed binding energy will be too low,
so you would expect 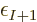 to underestimate the electron
affinity relatively badly. That is especially so since affinities
tend to be relatively small compared to ionization energies. Indeed
Szabo and Ostlund [46, p. 128] note that while many
neutral molecules will take up and bind a free electron, producing a
stable negative ion, the orbital energies almost always predict
negative binding energy, hence no stable ion.
to underestimate the electron
affinity relatively badly. That is especially so since affinities
tend to be relatively small compared to ionization energies. Indeed
Szabo and Ostlund [46, p. 128] note that while many
neutral molecules will take up and bind a free electron, producing a
stable negative ion, the orbital energies almost always predict
negative binding energy, hence no stable ion.
9.3.5.2 Asymptotic behavior
The exchange terms in the Hartree-Fock potential are not really a
potential, but an operator. It turns out that this makes a major
difference in how the probability of finding an electron decays with
distance from the system.
Consider again the Fock eigenvalue problem, but with the single-electron
Hamiltonian identified in terms of kinetic energy and nuclear attraction,
Now consider the question which of these terms dominate at large
distance from the system and therefore determine the large-distance
behavior of the solution.
The first term that can be thrown out is 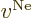 , the Coulomb
potential due to the nuclei; this potential decays to zero
approximately inversely proportional to the distance from the system.
(At large distance from the system, the distances between the nuclei
can be ignored, and the potential is then approximately the one of a
single point charge with the combined nuclear strengths.) Since
, the Coulomb
potential due to the nuclei; this potential decays to zero
approximately inversely proportional to the distance from the system.
(At large distance from the system, the distances between the nuclei
can be ignored, and the potential is then approximately the one of a
single point charge with the combined nuclear strengths.) Since
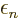 in the right hand side does not decay to zero, the
nuclear term cannot survive compared to it.
in the right hand side does not decay to zero, the
nuclear term cannot survive compared to it.
Similarly the third term, the Coulomb part of the Hartree-Fock
potential, cannot survive since it too is a Coulomb potential, just
with a charge distribution given by the orbitals in the inner product.
However, the final term in the left hand side, the exchange part of
the Hartree-Fock potential, is more tricky, because the various parts
of this sum have other orbitals outside of the inner product. This
term can still be ignored for the slowest-decaying spin-up and
spin-down states, because for them none of the other orbitals is any
larger, and the multiplying inner product still decays like a Coulomb
potential (faster, actually). Under these conditions the kinetic
energy will have to match the right hand side, implying
From this expression, it can also be seen that the 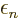 values
must be negative, or else the slowest decaying orbitals would not have
the exponential decay with distance of a bound state.
values
must be negative, or else the slowest decaying orbitals would not have
the exponential decay with distance of a bound state.
The other orbitals, however, cannot be less than the slowest decaying
one of the same spin by more than algebraic factors: the slowest
decaying orbital with the same spin appears in the exchange term sum
and will have to be matched. So, with the exchange terms included,
all orbitals normally decay slowly, raising the chances of finding
electrons at significant distances. The decay can be written as
 |
(9.30) |
where 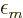 is the
is the  value of smallest magnitude
(absolute value) among all the orbitals with the same spin.
value of smallest magnitude
(absolute value) among all the orbitals with the same spin.
However, in the case that 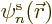 is spherically symmetric,
(i.e. an s state), exclude other s-states as possibilities for
is spherically symmetric,
(i.e. an s state), exclude other s-states as possibilities for
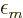 . The reason is a peculiarity of the Coulomb
potential that makes the inner product appearing in the exchange term
exponentially small at large distance for two orthogonal, spherically
symmetric states. (For the incurably curious, it is a result of
Maxwell’s first equation applied to a spherically symmetric
configuration like figure 13.1, but with multiple
spherically distributed charges rather than one, and the net charge
being zero.)
. The reason is a peculiarity of the Coulomb
potential that makes the inner product appearing in the exchange term
exponentially small at large distance for two orthogonal, spherically
symmetric states. (For the incurably curious, it is a result of
Maxwell’s first equation applied to a spherically symmetric
configuration like figure 13.1, but with multiple
spherically distributed charges rather than one, and the net charge
being zero.)
9.3.5.3 Hartree-Fock limit
The Hartree-Fock approximation greatly simplifies finding a
many-dimensional wave function. But really, solving the “eigenvalue
problems” (9.28) for the orbitals iteratively is not
that easy either. Typically, what one does is to write the orbitals
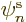 as sums of chosen single-electron functions
as sums of chosen single-electron functions
 . You can then precompute various integrals in
terms of those functions. Of course, the number of chosen
single-electron functions will have to be a lot more than the number
of orbitals
. You can then precompute various integrals in
terms of those functions. Of course, the number of chosen
single-electron functions will have to be a lot more than the number
of orbitals  ; if you are only using
; if you are only using  chosen functions, it
really means that you are choosing the orbitals
chosen functions, it
really means that you are choosing the orbitals 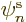 rather
than computing them.
rather
than computing them.
But you do not want to choose too many functions either, because the
required numerical effort will go up. So there will be an error
involved; you will not get as close to the true best orbitals as you
can. One thing this means is that the actual error in the ground
state energy will be even larger than true Hartree-Fock would give.
For that reason, the Hartree-Fock value of the ground state energy is
called the Hartree-Fock limit:
it is how close you
could come to the correct energy if you were able to solve the
Hartree-Fock equations exactly.
In short, to compute the Hartree-Fock solution accurately, you want to
select a large number of single-electron functions to represent the
orbitals. But don't start using zillions of them. The problem is
that even the exact Hartree-Fock solution still has a finite error; a
wave function cannot in general be described accurately using only a
single Slater determinant. So what would the point in computing the
very inaccurate numbers to ten digits accuracy?
9.3.5.4 Correlation energy
As the previous subsubsection noted, the Hartree-Fock solution, even
if computed exactly, will still have a finite error. You might think
that this error would be called something like “Hartree-Fock
error.” Or maybe “representation error“ or
single-determinant error,
since it is due to an
incomplete representation of the true wave function using a single
Slater determinant.
However, the Hartree-Fock error in energy is called “correlation energy.” The reason is because there is a
energizing correlation between the more impenetrable and poorly
defined your jargon, and the more respect you will get for doing all
that incomprehensible stuff.
And of course the word error
should never be used in
the first place, God forbid. Or those hated non-experts might figure
out that Hartree-Fock has an error in energy so big that it makes the
base approximation pretty much useless for chemistry.
To understand what physicists are referring to with
correlation,
reconsider the form of the Hartree-Fock
wave function, as described in subsection 9.3.1. It consisted
of a single Slater determinant. However, that Slater determinant in
turn consisted of a lot of Hartree products, the first of which was
The other Hartree products were different only in the order in which
the electrons appear in the product. And since the electrons are all
the same, the order does not make a difference: each of these Hartree
products has the same expectation energy. Each also satisfies the
Pauli exclusion principle but, by itself, not the
antisymmetrization requirement.
Now, consider what the Born statistical interpretation says about the
single Hartree product above. It says that the probability of
electron 1 to be within a vicinity of volume 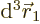 around a
given position
around a
given position 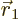 with given spin
with given spin 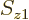 , and electron 2
to be within a vicinity of volume
, and electron 2
to be within a vicinity of volume 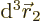 around a given position
around a given position
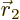 with given spin
with given spin 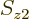 , etcetera, is given by
, etcetera, is given by
This takes the form of a probability for electron 1 to be in the given
state that is independent of where the other electrons are,
times a probability for electron 2 to be in the given state that is
independent of where the other electrons are, etcetera. In
short, in a single Hartree product the electrons do not care where the
other electrons are. Their positions are
uncorrelated.
Uncorrelated positions would be OK if the electrons did not repel each
other. In that case, each electron would indeed not care where the
other electrons are. Then all Hartree products would have the same
energy, which would also be the energy of the complete Slater
determinant.
But electrons do repel each other. So, if electron 1 is at a given
position 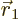 , electron 2 can reduce its potential energy by
preferring positions farther away from that position. It cannot
overdo it, as that will increase its kinetic energy too much, but
there is some room for improvement. So the exact wave function will
have correlations between the positions of different electrons.
Based on arguments like that, physicists then come up with the term
correlation energy.
, electron 2 can reduce its potential energy by
preferring positions farther away from that position. It cannot
overdo it, as that will increase its kinetic energy too much, but
there is some room for improvement. So the exact wave function will
have correlations between the positions of different electrons.
Based on arguments like that, physicists then come up with the term
correlation energy.
Not so fast, physicists! For one, a Slater determinant is not a
single Hartree product but already includes some electron
correlations. Also, correlation energy
is not the
same as “error in energy caused by incorrect
correlations.” And “error in energy caused by incorrect
correlations” is not the same as “error in energy for an
incorrect solution, including incorrect correlations.” And the
last is what the Hartree-Fock error really is. Note that while there
is some rough qualitative relation between potential energy and
electron position correlations, you cannot find the potential energy
by pontificating about electrons trying to stay away from each other.
And the correct energy state is found by delicately balancing subtle
reductions in potential energy against subtle increases in kinetic
energy. The kinetic energy does not even care about electron
correlations. However, the kinetic energy is wrong too when applied
on a single Slater determinant.
See note {N.18} for more.
9.3.5.5 Configuration interaction
Since the base Hartree-Fock approximation has an error that is far too
big for typical chemistry applications, the next question is what can
be done about it. The basic answer is simple: use more that  orbitals, i.e. single-particle wave functions. As already noted in
section 5.7, if you include enough orthonormal basis
functions, using all their possible Slater determinants, you can
approximate any function to arbitrary accuracy.
orbitals, i.e. single-particle wave functions. As already noted in
section 5.7, if you include enough orthonormal basis
functions, using all their possible Slater determinants, you can
approximate any function to arbitrary accuracy.
After the  , (or
, (or 
 2 in the restricted closed-shell case,)
spatial orbitals have been found, the Hartree-Fock operator becomes
just a Hermitian operator, and can be used to compute further
orthonormal orbitals
2 in the restricted closed-shell case,)
spatial orbitals have been found, the Hartree-Fock operator becomes
just a Hermitian operator, and can be used to compute further
orthonormal orbitals 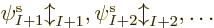 . You can
add these to the mix, say to get a better approximation to the true
ground state wave function of the system.
. You can
add these to the mix, say to get a better approximation to the true
ground state wave function of the system.
You might want to try to start small. If you include just one more
orbital 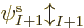 , you can already form
, you can already form  more Slater
determinants: you can replace any of the
more Slater
determinants: you can replace any of the  orbitals in the original
determinant by the new function
orbitals in the original
determinant by the new function 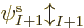 . So you can now
approximate the true wave function by the more general expression
. So you can now
approximate the true wave function by the more general expression
where the coefficients  are to be chosen to
approximate the ground state energy more closely and
are to be chosen to
approximate the ground state energy more closely and 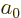 is a
normalization constant.
is a
normalization constant.
The additional  Slater determinants are called “excited determinants”. For example, the first excited state
Slater determinants are called “excited determinants”. For example, the first excited state
is like a state where you excited an electron out of the lowest state
 into an elevated energy state
into an elevated energy state 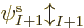 .
.
(However, note that if you really wanted to satisfy the variational
requirement 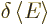
 0 for such a state, you would have to
recompute the orbitals from scratch, using
0 for such a state, you would have to
recompute the orbitals from scratch, using 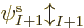 in the Fock
operator instead of
in the Fock
operator instead of  . That is not what you want to do
here; you do not want to create totally new orbitals, just more of
them.)
. That is not what you want to do
here; you do not want to create totally new orbitals, just more of
them.)
It may seem that this must be a winner: as much as  more
determinants to further minimize the energy. Unfortunately, now you
pay the price for doing such a great job with the single determinant.
Since, hopefully, the Slater determinant is the best single
determinant that can be formed, any changes that are equivalent to
simply changing the determinant's orbitals will do no good. And it
turns out that the
more
determinants to further minimize the energy. Unfortunately, now you
pay the price for doing such a great job with the single determinant.
Since, hopefully, the Slater determinant is the best single
determinant that can be formed, any changes that are equivalent to
simply changing the determinant's orbitals will do no good. And it
turns out that the 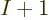 -determinant wave function above is
equivalent to the single-determinant wave function
-determinant wave function above is
equivalent to the single-determinant wave function
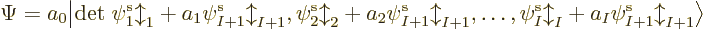
as you can check with some knowledge of the properties of
determinants. Since you already have the best single determinant, all
your efforts are going to be wasted if you try this.
You might try forming another set of  excited determinants by
replacing one of the orbitals in the original Hartree-Fock determinant
by
excited determinants by
replacing one of the orbitals in the original Hartree-Fock determinant
by 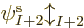 instead of
instead of 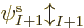 , but the fact is that
the infinitesimal variational condition
, but the fact is that
the infinitesimal variational condition 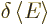
 0 is
still going to be satisfied when the wave function is the original
Hartree-Fock one. For small changes in wave function, the additional
determinants can still be pushed inside the Hartree-Fock one. To
ensure a decrease in energy, you want to include determinants that
allow a nonzero decrease in energy even for small changes from the
original determinant, and that requires
0 is
still going to be satisfied when the wave function is the original
Hartree-Fock one. For small changes in wave function, the additional
determinants can still be pushed inside the Hartree-Fock one. To
ensure a decrease in energy, you want to include determinants that
allow a nonzero decrease in energy even for small changes from the
original determinant, and that requires doubly
excited
determinants, in which two different original states are replaced by
excited ones like 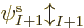 and
and 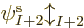 .
.
Note that you can form 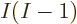 such determinants; the number of
determinants rapidly explodes when you include more and more orbitals.
And a mathematically convergent process would require an
asymptotically large set of orbitals, compare chapter
5.7. How big is your computer?
such determinants; the number of
determinants rapidly explodes when you include more and more orbitals.
And a mathematically convergent process would require an
asymptotically large set of orbitals, compare chapter
5.7. How big is your computer?
Most people would probably call improving the wave function
representation using multiple Slater determinants something like
multiple-determinant representation,
or
excited-determinant correction.
. However, it is
called configuration interaction.
The reason is that
every hated non-expert will wonder whether the physicist is talking
about the configuration of the nuclei or the electrons, and what it is
interacting with.
(Actually, configuration
refers to the
practitioner configuring
all those
determinants, no kidding. The interaction is with the computer used
to do so. Suppose you were creating the numerical mesh for some
finite difference or finite element computation. If you called that
configuration interaction
instead of “mesh
generation,” because it required you to
configure
all those mesh points through interacting
with your computer, some people might doubt your sanity. But in
physics, the standards are not so high.)
![]()
![]()
![]() ,
,![]() .
.![]()
![]() ,
,![]() .
.![]()
![]() ;
;![]()
![]()
![]() ,
,![]() .
.![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
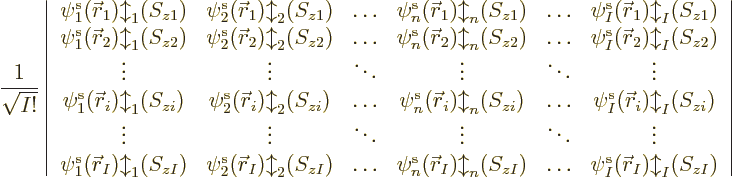
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]() ,
,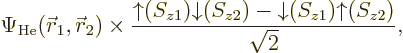
![]() -
-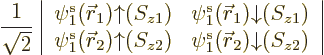

![]()
![]() .
.![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]() ,
,![]() ,
,![]()
![]()
![]()
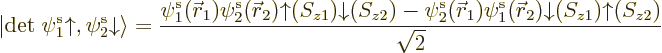

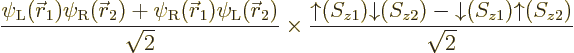

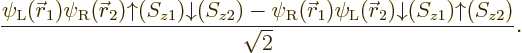
![]()
![]()

![]()
![]() ,
,![]()
![]()
![]() )
)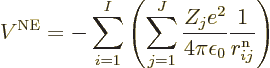
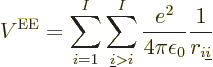
![]()
![]()
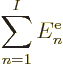
![]() :
: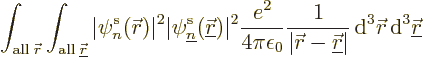
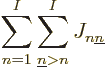
![]()
![]()
![]()
![]()
![]()
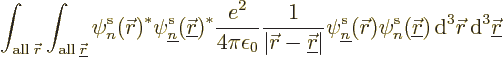
![]()
![]()
![]()
![]()
![]()
![]() :
: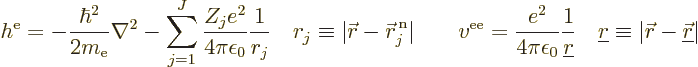
![]() .
.![]() :
: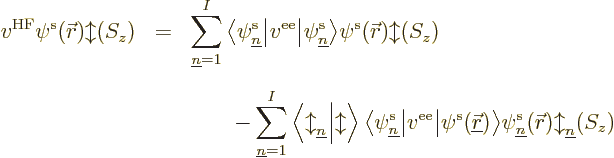
![]()
![]()
![]() .
.![]()
![]()
![]()
![]() ,
,![]() ,
,![]() ,
,![]()
![]() ?
?![]()
![]()
![]()
![\begin{displaymath}
\begin{array}[b]{l}
\displaystyle
h^{\rm e}\pe n/{\skew0\...
...w0\vec r}///
= \epsilon_n \pe n/{\skew0\vec r}///
\end{array}\end{displaymath}](img2111.gif)
![]()
![]() ,
,![]()
![]() .
.![]()
![]() ,
,![]() ,
,![]()
![]() .
.![]()
![]()
![]() -
-![]() -
-![]()
![]()
![]() -
-![]() -
-![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]() -
-![]()
![\begin{displaymath}
\begin{array}[b]{l}
\displaystyle
- \frac{\hbar^2}{2m_{\r...
...w0\vec r}///
= \epsilon_n \pe n/{\skew0\vec r}///
\end{array}\end{displaymath}](img2121.gif)
![]() ,
,![]()
![]()
![]() .
.![]()
![]() .
.![]() ;
;![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,
![]() ,
,![]()
![]() ,
,![]()
![]()
![]() .
.![]() ,
,![]()
![]()
![]() .
.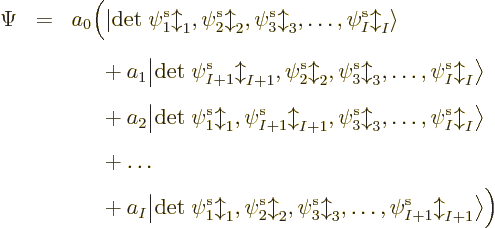
![]()
![]()
![]()
![]()
![]() .
.![]()
![]() -
-![]()
![]()
![]() ,
,![]()
![]()
![]()
![]() .
.![]()