|
|
|
|
|
Next: 13. Electromagnetism |
|
Relativity threw up some road blocks when quantum mechanics was first formulated, especially for the particles physicist wanted to look at most, electrons. This section explains some of the ideas.
You will need a good understanding of linear algebra to really follow the reasoning. A summary of the Dirac equation that is less heavy on the linear algebra can be found in {A.44}.
For zero spin particles, including relativity appears to be simple.
The classical kinetic energy Hamiltonian for a particle in free space,
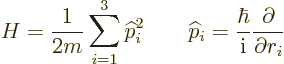
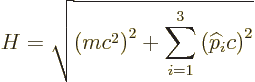
![\begin{displaymath}
\left[
\left(m c^2\right)^2 + \sum_{i=1}^3 \left({\widehat p}_i c\right)^2
\right]\psi
=E^2\psi
\end{displaymath}](img2801.gif)
Unfortunately, throwing a dash of spin into this recipe simply does
not seem to work in a convincing way. Apparently, that very problem
led Schrödinger to limit himself to the nonrelativistic case. It is hard to
formulate simple equations with an ugly square root in your way, and
surely, you will agree, the relativistic equation for something so
very fundamental as an electron in free space should be simple and
beautiful like other fundamental equations in physics. (Can you be
more concise than ![]()
![]()
![]()
![]()
![]()
![]() ?
?
So P.A.M. Dirac boldly proposed that for a particle like
an electron, (and other spin ![]()
But here is the key: while this does not work for plain numbers, Dirac
showed it is possible if you are dealing with matrices, tables
of numbers. In particular, it works if the coefficients are given by

Now if the Hamiltonian is a 4 ![]()
That was of course a curious thing. Consider an electron in what otherwise is an empty vacuum. What prevents the electron from spontaneously transitioning to the negative rest mass state, releasing twice its rest mass in energy? Dirac concluded that what is called empty vacuum should in the mathematics of quantum mechanics be taken to be a state in which all negative energy states are already filled with electrons. Clearly, that requires the Pauli exclusion principle to be valid for electrons, otherwise the electron could still transition into such a state. According to this idea, nature really does not have a free choice in whether to apply the exclusion principle to electrons if it wants to create a universe as we know it.
But now consider the vacuum without the electron. What prevents you
from adding a big chunk of energy and lifting an electron out of a
negative rest-mass state into a positive one? Nothing, really. It
will produce a normal electron and a place in the vacuum where an
electron is missing, a hole
. And here finally Dirac's
boldness appears to have deserted him; he shrank from proposing that
this hole would physically show up as the exact antithesis of the
electron, its anti-particle, the positively charged positron. Instead
Dirac weakly pointed the finger at the proton as a possibility.
Pure cowardice,
he called it later. The positron that
his theory really predicted was subsequently discovered anyway. (It
had already been observed earlier, but was not recognized.)
The reverse of the production of an electron/positron pair is pair annihilation, in which a positron and an electron eliminate each other, creating two gamma-ray photons. There must be two, because viewed from the combined center of mass, the net momentum of the pair is zero, and momentum conservation says it must still be zero after the collision. A single photon would have nonzero momentum, you need two photons coming out in opposite directions. However, pairs can be created from a single photon with enough energy if it happens in the vicinity of, say, a heavy nucleus: a heavy nucleus can absorb the momentum of the photon without picking up much velocity, so without absorbing too much of the photon's energy.
The Dirac equation also gives a very accurate prediction of the
magnetic moment of the electron, section 13.4, though
the quantum electromagnetic field affects the electron and introduces
a correction of about a tenth of a percent. But the importance of the
Dirac equation was much more than that: it was the clue to our
understanding how quantum mechanics can be reconciled with relativity,
where particles are no longer absolute, but can be created out of
nothing or destroyed according to the mass-energy relation ![]()
![]()
![]() ,
,
Dirac was a theoretical physicist at Cambridge University, but he moved to Florida in his later life to be closer to his elder daughter, and was a professor of physics at the Florida State University when I got there. So it gives me some pleasure to include the Dirac equation in my text as the corner stone of relativistic quantum mechanics.