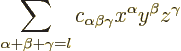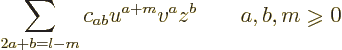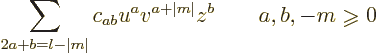| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
Subsections
D.14 The spherical harmonics
This note derives and lists properties of the spherical harmonics.
D.14.1 Derivation from the eigenvalue problem
This analysis will derive the spherical harmonics from the eigenvalue
problem of square angular momentum of chapter 4.2.3. It
will use similar techniques as for the harmonic oscillator solution,
{D.12}.
The imposed additional requirement that the spherical harmonics
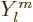 are eigenfunctions of
are eigenfunctions of 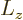 means that they are of the form
means that they are of the form
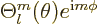 where function
where function  is still to be determined. (There is also an arbitrary dependence on
the radius
is still to be determined. (There is also an arbitrary dependence on
the radius  , but it does not have anything to do with angular
momentum, hence is ignored when people define the spherical
harmonics.) Substitution into
, but it does not have anything to do with angular
momentum, hence is ignored when people define the spherical
harmonics.) Substitution into 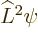

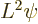 with
with 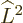 as in (4.22) yields an ODE (ordinary differential equation)
for
as in (4.22) yields an ODE (ordinary differential equation)
for  :
:
It is convenient define a scaled square angular momentum by


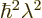 so that you can divide away the
so that you can divide away the 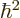 from
the ODE.
from
the ODE.
More importantly, recognize that the solutions will likely be in terms
of cosines and sines of  , because they should be
periodic if
, because they should be
periodic if  changes by
changes by  . If you want to use
power-series solution procedures again, these transcendental functions
are bad news, so switch to a new variable
. If you want to use
power-series solution procedures again, these transcendental functions
are bad news, so switch to a new variable 

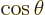 . At the very least, that will reduce things to
algebraic functions, since
. At the very least, that will reduce things to
algebraic functions, since 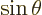 is in terms of
is in terms of 

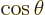 equal to
equal to  . Converting the ODE to the
new variable
. Converting the ODE to the
new variable  , you get
, you get
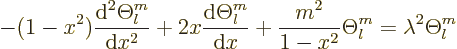
As you may guess from looking at this ODE, the solutions  are likely to be problematic near
are likely to be problematic near 

 , (physically,
near the
, (physically,
near the  -axis where
-axis where 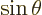 is zero.) If you examine the
solution near those points by defining a local coordinate
is zero.) If you examine the
solution near those points by defining a local coordinate 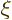 as in
as in


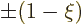 , and then deduce the leading term in the
power series solutions with respect to
, and then deduce the leading term in the
power series solutions with respect to 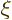 , you find that it
is either
, you find that it
is either  or
or  , (in the special case that
, (in the special case that

 0, that second solution turns out to be
0, that second solution turns out to be 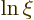 .)
Either way, the second possibility is not acceptable, since it
physically would have infinite derivatives at the
.)
Either way, the second possibility is not acceptable, since it
physically would have infinite derivatives at the  -axis and a
resulting expectation value of square momentum, as defined in chapter
4.4.3, that is infinite. You need to have that
-axis and a
resulting expectation value of square momentum, as defined in chapter
4.4.3, that is infinite. You need to have that  behaves as
behaves as  at each end, so in terms of
at each end, so in terms of  it must have a
factor
it must have a
factor  near
near 
 1 and
1 and 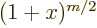 near
near 

 1. The two factors multiply to
1. The two factors multiply to 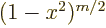 and so
and so  can be written as
can be written as 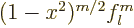 where
where 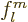 must have finite
values at
must have finite
values at 
 1 and
1 and 

 1.
1.
If you substitute 

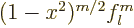 into the ODE
for
into the ODE
for  , you get an ODE for
, you get an ODE for 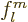 :
:
Plug in a power series, 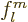

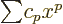 , to get,
after clean up,
, to get,
after clean up,
Using similar arguments as for the harmonic oscillator, you see that
the starting power will be zero or one, leading to basic solutions
that are again odd or even. And just like for the harmonic
oscillator, you must again have that the power series terminates; even
in the least case that 
 0, the series for
0, the series for 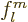 at
at 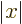
 1 is
like that of
1 is
like that of 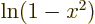 and will not converge to the finite value
stipulated. (For rigor, use Gauss’s test.)
and will not converge to the finite value
stipulated. (For rigor, use Gauss’s test.)
To get the series to terminate at some final power 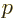

 , you must have according to the above equation that
, you must have according to the above equation that
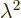

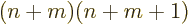 , and if you decide to call
, and if you decide to call
 the azimuthal quantum number
the azimuthal quantum number  , you have
, you have 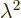

 where
where 
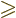
 since
since 

 and
and
 , like any power
, like any power 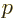 , is greater or equal to zero.
, is greater or equal to zero.
The rest is just a matter of table books, because with 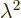

 , the ODE for
, the ODE for 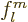 is just the
is just the  -th
derivative of the differential equation for the
-th
derivative of the differential equation for the  Legendre
polynomial, [41, 28.1], so the
Legendre
polynomial, [41, 28.1], so the 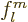 must be just the
must be just the
 -th derivative of those polynomials. In fact, you can now
recognize that the ODE for the
-th derivative of those polynomials. In fact, you can now
recognize that the ODE for the  is just Legendre's
associated differential equation [41, 28.49], and that
the solutions that you need are the associated Legendre functions of
the first kind [41, 28.50].
is just Legendre's
associated differential equation [41, 28.49], and that
the solutions that you need are the associated Legendre functions of
the first kind [41, 28.50].
To normalize the eigenfunctions on the surface area of the unit
sphere, find the corresponding integral in a table book, like
[41, 28.63]. As mentioned at the start of this long and
still very condensed story, to include negative values of  ,
just replace
,
just replace  by
by  . There is one additional issue,
though, the sign pattern. In order to simplify some more advanced
analysis, physicists like the sign pattern to vary with
. There is one additional issue,
though, the sign pattern. In order to simplify some more advanced
analysis, physicists like the sign pattern to vary with  according
to the so-called
according
to the so-called ladder operators.
That requires,
{D.64}, that starting from 
 0, the spherical
harmonics for
0, the spherical
harmonics for 
 0 have the alternating sign pattern of the
0 have the alternating sign pattern of the
ladder-up operator,
and those for 
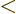 0 the
unvarying sign of the
0 the
unvarying sign of the ladder-down operator.
Physicists
will still allow you to select your own sign for the 
 0
state, bless them.
0
state, bless them.
The final solution is
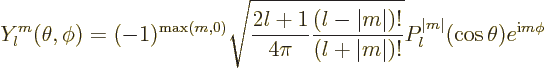 |
(D.5) |
where the properties of the associated Legendre functions of the first
kind 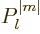 can be found in table books like
[41, pp. 162-166]. This uses the following definition
of the associated Legendre polynomials:
can be found in table books like
[41, pp. 162-166]. This uses the following definition
of the associated Legendre polynomials:
where 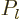 is the normal Legendre polynomial. Needless to say, some
other authors use different definitions, potentially putting in a
factor
is the normal Legendre polynomial. Needless to say, some
other authors use different definitions, potentially putting in a
factor  .
.
D.14.2 Parity
One special property of the spherical harmonics is often of interest:
their “parity.” The parity of a wave function is 1, or even, if the
wave function stays the same if you replace  by
by 
 .
The parity is
.
The parity is  1, or odd, if the wave function stays the same save
for a sign change when you replace
1, or odd, if the wave function stays the same save
for a sign change when you replace  by
by 
 . It turns
out that the parity of the spherical harmonics is
. It turns
out that the parity of the spherical harmonics is 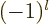 ; so
it is
; so
it is  1, odd, if the azimuthal quantum number
1, odd, if the azimuthal quantum number  is odd, and 1,
even, if
is odd, and 1,
even, if  is even.
is even.
To see why, note that replacing  by
by 
 means in spherical
coordinates that
means in spherical
coordinates that  changes into
changes into  and
and  into
into
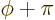 . According to trig, the first changes
. According to trig, the first changes 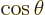 into
into 
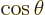 . That leaves
. That leaves 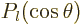 unchanged
for even
unchanged
for even  , since
, since 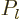 is then a symmetric function, but it
changes the sign of
is then a symmetric function, but it
changes the sign of 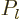 for odd
for odd  . So the sign change is
. So the sign change is
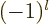 . The value of
. The value of  has no effect, since while the
factor
has no effect, since while the
factor 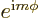 in the spherical harmonics produces a factor
in the spherical harmonics produces a factor
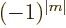 under the change in
under the change in  ,
,  also puts
also puts  derivatives on
derivatives on 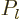 , and each derivative produces a
compensating change of sign in
, and each derivative produces a
compensating change of sign in 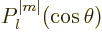 .
.
D.14.3 Solutions of the Laplace equation
The Laplace equation
is
Solutions 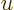 to this equation are called “harmonic functions.” In spherical coordinates, the
Laplace equation has solutions of the form
to this equation are called “harmonic functions.” In spherical coordinates, the
Laplace equation has solutions of the form
This is a complete set of solutions for the Laplace equation inside a
sphere. Any solution 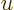 of the Laplace equation inside a sphere is a
linear combination of these solutions.
of the Laplace equation inside a sphere is a
linear combination of these solutions.
As you can see in table 4.3, each solution above is a power
series in terms of Cartesian coordinates.
For the Laplace equation outside a sphere, replace 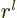 by
1
by
1
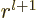 in the solutions above. Note that these solutions are not
acceptable inside the sphere because they blow up at the origin.
in the solutions above. Note that these solutions are not
acceptable inside the sphere because they blow up at the origin.
To check that these are indeed solutions of the Laplace equation, plug
them in, using the Laplacian in spherical coordinates given in
(N.5). Note here that the angular derivatives can be
simplified using the eigenvalue problem of square angular momentum,
chapter 4.2.3.
D.14.4 Orthogonal integrals
The spherical harmonics are orthonormal on the unit sphere:
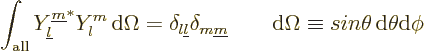 |
(D.6) |
Here 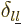 is defined to be 0 if
is defined to be 0 if  and
and  are
different, and 1 if they are equal, and similar for
are
different, and 1 if they are equal, and similar for
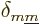 . In other words, the integral above is 1 if
. In other words, the integral above is 1 if 

 and
and 

 , and 0 in every other case.
This expresses physically that the spherical harmonics, as
eigenfunctions of the Hermitian
, and 0 in every other case.
This expresses physically that the spherical harmonics, as
eigenfunctions of the Hermitian  and square angular momentum
operators, are orthonormal. Mathematically, it allows you to
integrate each spherical harmonic separately and quickly when you are
finding
and square angular momentum
operators, are orthonormal. Mathematically, it allows you to
integrate each spherical harmonic separately and quickly when you are
finding 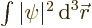 for a wave function
for a wave function  expressed in
terms of spherical harmonics.
expressed in
terms of spherical harmonics.
Further
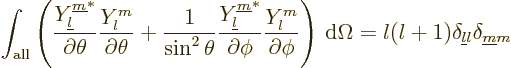 |
(D.7) |
This expression simplifies your life when you are finding the
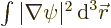 for a wave function
for a wave function  expressed in
terms of spherical harmonics.
expressed in
terms of spherical harmonics.
See the notations for more on spherical coordinates and
 .
.
To verify the above expression, integrate the first term in the
integral by parts with respect to  and the second term with
respect to
and the second term with
respect to  to get
to get
and then apply the eigenvalue problem of chapter 4.2.3.
D.14.5 Another way to find the spherical harmonics
There is a more intuitive way to derive the spherical harmonics: they
define the power series solutions to the Laplace equation. In
particular, each  is a different power series solution
is a different power series solution 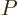 of the Laplace equation
of the Laplace equation 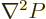
 0 in Cartesian coordinates.
Each takes the form
0 in Cartesian coordinates.
Each takes the form
where the coefficients 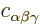 are such as to make the
Laplacian zero.
are such as to make the
Laplacian zero.
Even more specifically, the spherical harmonics are of the form
where the coordinates 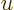

 and
and 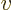

 serve to
simplify the Laplacian. That these are the basic power series
solutions of the Laplace equation is readily checked.
serve to
simplify the Laplacian. That these are the basic power series
solutions of the Laplace equation is readily checked.
To get from those power series solutions back to the equation for the
spherical harmonics, one has to do an inverse separation of variables
argument for the solution of the Laplace equation in a sphere in
spherical coordinates (compare also the derivation of the hydrogen
atom.) Also, one would have to accept on faith that the solution of
the Laplace equation is just a power series, as it is in 2D, with no
additional nonpower terms, to settle completeness. In other words,
you must assume that the solution is analytic.
D.14.6 Still another way to find them
The simplest way of getting the spherical harmonics is probably the
one given later in derivation {D.64}.
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]() :
: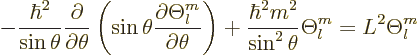
![]() ,
,![]()
![]() .
.![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]() .
.![]() ,
,![]()
![]()
![]()
![]() ,
,![]() -
-![]()
![]()
![]()
![]()
![]() ,
,![]() ,
,![]()
![]() ,
,![]()
![]()
![]() .
.![]() -
-![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 1
1![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 1
1![]()
![]()
![]()
![]() ,
,![]() :
:![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]() ,
,![]()
![]()
![]() ,
,![]()
![]() -
-![]()
![]()
![]() -
-![]()
![]() ,
,![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]() 1
1![]()
![]()
![]() .
.![]() ;
;![]() 1
1![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]() .
.![]()
![]() ,
,![]()
![]()
![]() .
.![]() .
.![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]() .
.![]()
![]()
![]()
![]() .
.![]()
![]()
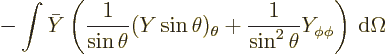
![]()
![]()
![]()
![]()