|
|
|
|
|
Next: 7.2 Time Variation of Expectation Values |
|
In Newtonian mechanics, Newton's second law states that the linear
momentum changes in time proportional to the applied force;
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
The Schrödinger equation says that the time derivative of the wave function is obtained by applying the
Hamiltonian on it. More precisely:
An equivalent and earlier formulation of quantum mechanics was given by Heisenberg, {A.12}. However, the Schrödinger equation tends to be easier to deal with, especially in nonrelativistic applications. An integral version of the Schrödinger equation that is sometimes convenient is in {A.13}.
The Schrödinger equations is nonrelativistic. The simplest relativistic version is called the Klein-Gordon equation. A discussion is in addendum {A.14}. However, relativity introduces a fundamentally new issue: following Einstein’s mass-energy equivalence, particles may be created out of pure energy or destroyed. To deal with that, you typically need a formulation of quantum mechanics called quantum field theory. A very brief introduction is in addendum {A.15}.
Key Points
- The Schrödinger equation describes the time evolution of the wave function.
- The time derivative is proportional to the Hamiltonian.
The solution to the Schrödinger equation can immediately be given for most cases of interest. The only condition that needs to be satisfied is that the Hamiltonian depends only on the state the system is in, and not explicitly on time. This condition is satisfied in all cases discussed so far, including the particle in a box, the harmonic oscillator, the hydrogen and heavier atoms, and the molecules, so the following solution applies to them all:
To satisfy the Schrödinger equation, write the wave functionin terms of whatever are the energy eigenfunctions of the Hamiltonian,
| (7.2) |
Then the coefficientsmust evolve in time as complex exponentials:
for every combination of quantum numbers.
In short, you get the wave function for arbitrary times by taking the
initial wave function and shoving in additional factors
![]() .
.![]()
![]()
Consider how this works out for the electron in the hydrogen atom.
Here each spatial energy state ![]()
![]() ,
,![]() ,
,![]() ,
,![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]() ,
,
The most general wave function for the hydrogen atom is then:

The given solution in terms of eigenfunctions covers most cases of interest, but as noted, it is not valid if the Hamiltonian depends explicitly on time. That possibility arises when there are external influences on the system; in such cases the energy does not just depend on what state the system itself is in, but also on what the external influences are like at the time.
Key Points
- Normally, the coefficients of the energy eigenfunctions must be proportional to
.
The energy of a photon is ![]()
![]()
![]()
For the one-dimensional harmonic oscillator, the energy eigenvalues are
Now classically, the harmonic oscillator has a natural frequency ![]() .
.![]()
![]() ,
,![]() ;
;![]()
![]()
Write the full wave function for a one-dimensional harmonic oscillator. Formulae are in chapter 4.1.2.
The Schrödinger equation implies that the energy of a system is conserved, assuming that there are no external influences on the system.
To see why, consider the general form of the wave function:
According to chapter 3.4, the square magnitudes ![]()
For example, a wave function for a hydrogen atom at the excited energy
level ![]()
This is an important example, because it also illustrates that an excited atom will stay excited for all time if left alone. That is an apparent contradiction because, as discussed in chapter 4.3, the above excited atom will eventually emit a photon and transition back to the ground state. Even if you put it in a sealed box whose interior is at absolute zero temperature, it will still decay.
The explanation for this apparent contradiction is that an atom is never truly left alone. Simply put, even at absolute zero temperature, quantum uncertainty in energy allows an electromagnetic photon to pop up that perturbs the atom and causes the decay. (To describe more precisely what happens is a major objective of this chapter.)
Returning to the unperturbed atom, you may wonder what happens to
energy conservation if there is uncertainty in energy. In that case,
what does not change with time are the probabilities of measuring the
possible energy levels. As an arbitrary example, the following wave
function describes a case of an unperturbed hydrogen atom whose energy
has a 50/50 chance of being measured as ![]() ,
,![]() ,
,
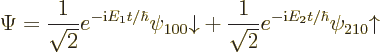
You can turn the observations of this subsection also around. If an external effect changes the energy of a system, then clearly the probabilities of the individual energies must change. So then the coefficients of the energy eigenfunctions cannot be simply vary exponentially with time as they do for the unperturbed systems discussed above.
Key Points
- Energy conservation is a fundamental consequence of the Schrödinger equation.
- An isolated system that has a given energy retains that energy.
- Even if there is uncertainty in the energy of an isolated system, still the probabilities of the various energies do not change with time.
The quest for the dynamical implications of the Schrödinger equation
must start with the simplest case. That is the case in which there is
only a single energy eigenfunction involved. Then the wave function
is of the form
stationary states.Systems in their ground state are of this type.
To see why these states are called stationary, note first of all that
the energy of the state is ![]()
But energy is not the only thing that does not change in time.
According to the Born interpretation, chapter 3.1, the
square magnitude of the wave function of a particle gives the
probability of finding the particle at that position and time. Now
the square magnitude of the wave function above is
For example, consider the case of the particle in a pipe of chapter
3.5. If the particle is in the ground state, its wave
function is of the form
The relative probability for where the particle may be found can be shown as grey tones:
The bottom line is that this picture is the same for all time.
If the wave function is purely the first excited state
![]() ,
,
And it is not just position that does not change. Neither do linear
or angular momentum, kinetic energy, etcetera. That can be easily
checked. The probability for a specific value of any physical
quantity is given by
And if probabilities do not change, then neither do expectation values, uncertainties, etcetera. No physically meaningful quantity changes with time.
Hence it is not really surprising that none of the energy eigenfunctions derived so far had any resemblance to the classical Newtonian picture of a particle moving around. Each energy eigenfunction by itself is a stationary state. There is no change in the probability of finding the particle regardless of the time that you look. So how could it possibly resemble a classical particle that is at different positions at different times?
To get time variations of physical quantities, states of different energy must be combined. In other words, there must be uncertainty in energy.
Key Points
- States of definite energy are stationary states.
- To get nontrivial time variation of a system requires uncertainty in energy.
The previous subsections discussed the solution for systems in which the Hamiltonian does not explicitly depend on time. Typically that means isolated systems, unaffected by external effects, or systems for which the external effects are relatively simple. If the external effects produce a time-dependent Hamiltonian, things get much messier. You cannot simply make the coefficients of the eigenfunctions vary exponentially in time as done in the previous subsections.
However, dealing with systems with time-dependent Hamiltonians can still be relatively easy if the Hamiltonian varies sufficiently slowly in time. Such systems are quasi-steady ones.
So physicists cannot call these systems quasi-steady; that would give
the secret away to these hated nonspecialists and pesky students.
Fortunately, physicists were able to find a much better name. They
call these systems adiabatic.
That works much better
because the word adiabatic
is a well-known term in
thermodynamics: it indicates systems that evolve fast enough
that heat conduction with the surroundings can be ignored. So, what
better name to use also for quantum systems that evolve slowly
enough that they stay in equilibrium with their surroundings? No one
familiar with even the most basic thermodynamics will ever guess what
it means.
As a simple example of an adiabatic system, assume that you have a particle in the ground state in a box. Now you change the volume of the box by a significant amount. The question is, will the particle still be in the ground state after the volume change? Normally there is no reason to assume so; after all, either way the energy of the particle will change significantly. However, the “adiabatic theorem” says that if the change is performed slowly enough, it will. The particle will indeed remain in the ground state, even though that state slowly changes into a completely different form.
If the system is in an energy state other than the ground state, the particle will stay in that state as it evolves during an adiabatic process. The theorem does assume that the energy is nondegenerate, so that the energy state is unambiguous. More sophisticated versions of the analysis exist to deal with degeneracy and continuous spectra.
A derivation of the theorem can be found in {D.34}. Some additional implications are in addendum {A.16}. The most important practical application of the adiabatic theorem is without doubt the Born-Oppenheimer approximation, which is discussed separately in chapter 9.2.
Key Points
- If the properties of a system in its ground state are changed, but slowly, the system will remain in the changing ground state.
- More generally, the
adiabaticapproximation can be used to analyze slowly changing systems.
- No, it has nothing to do with the normal use of the word
adiabatic.