|
|
|
|
|
Next: A.45 Fermi theory |
|
It is certainly dubious to describe beta decay nonrelativistically. Neutrinos are highly relativistic particles with almost zero rest mass. So [16, p. 258] rightly states that it is absurd to treat them nonrelativistically. Then he immediately proceeds to do it anyway. (But he confirms the results later using a proper analysis.)
One big problem is that relativistically, spin and orbital angular momentum become mixed-up. That problem was encountered earlier for the photon, which is an even more relativistic particle. Chapter 7.4.3 needed some contortions to talk around that problem.
But note that while the problem for the neutrino is qualitatively similar, the details are quite different. While the photon is a boson, the neutrino is a fermion. Fermions, unlike bosons, are described by the Dirac equation, chapter 12.12 versus {A.21}.
To understand the Dirac equation requires some linear algebra, in particular matrices. But to understand the discussion here, the information in the notations section should be plenty.
Consider first the Dirac Hamiltonian eigenvalue problem for the
electron and its antiparticle, the positron, in empty space. It is
simplest thought of as a system of two equations:
Pauli spin matrices.
In the nonrelativistic limit, ![]()
![]()
The nonrelativistic limit means mathematically that the rest mass
energies ![]()
![]() .
.
If you improve the accuracy of the nonrelativistic approximations a
bit using some mathematical manipulation, the energy will also include
the classical kinetic energy. To see how that works, (without using
more proper matrix eigenvalue methods), premultiply the second
equation in (A.271) by ![]()
![]()
![]()
![]()
![]() .
.
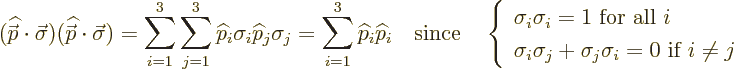
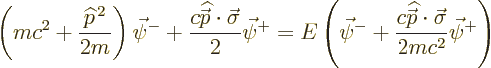
This expression can be rewritten as
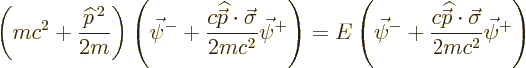
Derivation {D.81} shows how take this further, and do it rigorously using proper linear algebra procedures.
But this addendum is not really interested in the nonrelativistic
limit. Instead it is interested in the ultrarelativistic limit, where
it is the rest mass that is negligible compared to the kinetic energy.
And for zero rest mass, the Dirac eigenvalue problem (A.271)
becomes
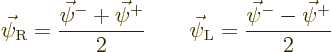
The mathematician Weyl first noted how remarkable these equations
really are. The equations for the two partial wave functions are not
coupled! Partial wave function ![]()
![]()
![]()
![]() .
.![]()
Reasonably speaking, these particles should be electrically neutral.
After all, their wave functions are equal combinations of
![]() ,
,![]() ,
,
There are a couple of problems however. The Dirac equation includes both the electron and the positron, the time-reversed electron. If you write an equation for a particle that does not inherently include a time-reversed partner, are you violating time-reversal symmetry?
The other problem is what happens if you look at nature in the mirror.
Or rather, what you really want to do is inversion:
swap the positive direction of all three axes in a Cartesian
coordinate system. This has the effect of creating a mirror image of
nature, since the coordinate system is now left-handed instead of
right-handed. And its effects are mathematically easier to describe.
First consider what happens to the original Dirac equation
(A.271). The linear momentum operator ![]()
![]() ,
,![]()
![]()
![]()
![]()
![]() ,
,
(These arguments as presented look at the dot product purely
algebraically. If you consider the gradient as a vector, there is an
additional sign change since the unit vectors change direction. But
the same holds for the ![]()
At face value then, the ![]()
Fortunately there is a loophole to save the mathematics of the Dirac
equation. It can be assumed that either the electron or the positron
has negative intrinsic
parity. In other words it can
be assumed that either nonrelativistic wave function changes sign
under inversion. You can check that if either ![]()
![]()
But now reconsider the Hamiltonian eigenvalue problem (A.273) for the neutrinos. The trick no longer works! If you can have one of these particles by itself, not tied to a partner, the physics is no longer the same when seen in the mirror.
There is an important consequence to that. If nature is the same when
seen in the mirror, there is a conserved mathematical quantity called
parity.
That is just like there is a conserved
quantity called angular momentum because nature behaves in the same
way when you look at it in a rotated coordinate system, chapter
7.3. What it boils down to is that Weyl was saying that
parity might not be conserved in nature.
At the time, Pauli lambasted Weyl for daring to suggest something so obviously stupid like that. However, Pauli lived long enough to learn in 1956 that experiments showed that indeed neutrinos do not conserve parity. (Weyl had already died.)
The fact that the Weyl Hamiltonians do not conserve parity can be
described more abstractly. Let ![]()
It is quite generally true that if an operator does not commute with the Hamiltonian, the corresponding quantity is not preserved. See for example chapter 4.5.1, 7.1.4 and {A.19}. So you might ask whether orbital angular momentum is preserved by the Weyl Hamiltonian. If you grind out the commutator of an orbital angular momentum component with the Weyl Hamiltonian using the rules of chapters 4.5.4 and 5.5.3, you find that you get something nonzero. So orbital angular momentum is not conserved by the Weyl neutrinos. That was no big surprise to physicists, because the Dirac equation does not conserve orbital angular momentum either. Similarly, if you work out the commutator of a component of spin, you find that spin is not preserved either.
However, if you add the two operators, you get the net angular momentum, orbital plus spin. That operator does commute with the Weyl Hamiltonians. So the Weyl Hamiltonians do conserve net angular momentum, like the Dirac equation does. That is very fortunate, because without doubt Pauli would have had a fit if Weyl had suggested that nature does not conserve net angular momentum.
But relativity does mix up orbital angular momentum with spin. Often this book describes particles as being in states of specific orbital angular momentum with specific values of the spin. For example, that is how the nonrelativistic hydrogen atom was described, chapter 4.3. Such a description is not really justified for particles at relativistic speeds. Fortunately the electron in a hydrogen atom has a kinetic energy much less than its rest mass energy. Things are much worse in beta decay, where the neutrino is emitted at almost the speed of light.
You might ask what else the Weyl Hamiltonians commute with. It can be seen that they commute with the linear momentum operators: different linear momentum operators commute because basically they are just derivatives, and spin commutes with nonspin. Different spin components do not commute, but everything commutes with itself. Since the Hamiltonian only involves the spin component in the direction of the linear momentum, (because of the dot product), the Hamiltonian commutes with the spin in that direction.
It is instructive to form a mental picture of these neutrinos. According to the above, the neutrinos can be in states with definite linear momentum and with definite spin in the direction of that linear momentum. In those states the neutrinos move in a specific direction and also rotate around an axis in the same direction. You can think of it macroscopically as screws; screws too rotate around their axis of motion while they move in or out of their hole.
Now there are two kinds of screws. Normal,
right-handed,
screws move into the hole if you rotate
them clockwise with a screwdriver. Some special applications use
left-handed
screws, which are machined so that they
move into the hole when you rotate them counter-clockwise. (One of
the screws that keep the pedals on a bicycle is normally a left-handed
screw, to prevent you from loosening it up when pedaling.)
Experiments show that all antineutrinos observed in a normal lab setting act like right-handed screws. Neutrinos act like left-handed screws. Since a right-handed screw turns into a left-handed screw when seen in a mirror, nature is not the same when seen in a mirror. If, say, a beta decay is observed in a mirror, the antineutrino that comes out is left-handed, rather than right-handed as it should.
(Using arguments like in {D.70}, it can be seen that
![]()
![]()
Note that theoretical physicists do not know about screws. So they
came up with a different way to express that antineutrinos are
right-handed like normal screws, while neutrinos are left-handed.
They call the component of spin in the direction of motion, scaled so
that its values are ![]() ,
,![]() 1
1
It is ironic that Pauli in turn did not live long enough to learn that Weyl’s neutrinos were wrong on at least one major count. Around 1998, experiments found that neutrinos and antineutrinos are not massless as was long thought. Their mass is extremely tiny, (far too tiny to be accurately measured by experimental methods available at the time of writing), but it is not zero.
Fundamentally, it makes a big difference, because then their speed must be less than the speed of light. Hypothetically, an observer can then move with a speed faster than some antineutrino produced in a lab. The antineutrino then seems to go backward for that observer. Since the spin is still in the same direction, the observer sees a left-handed antineutrino, not a right-handed one. So the handedness, or helicity, of antineutrinos, and similarly neutrinos, is not fundamental. A process like the beta decay of an nucleus moving at a speed extremely close to the speed of light could produce a left-handed antineutrino trailing the nucleus. But since this does not happen for a nucleus at rest, nature is still not the same when seen in the mirror.
At the time of writing, the precise nature of neutrinos is not yet fully understood. Usually, it is assumed that neutrinos are distinct from antineutrinos. Neutrinos for which that is true are called Dirac neutrinos. However, so-called Majorana neutrinos would be their own antiparticles; neutrinos and antineutrinos would simply differ in the spin state.