| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
Subsections
D.43 Multipole derivations
This derives the multipole matrix elements corresponding to a single
particle in an atom or nucleus. These will normally still need to be
summed over all particles.
Both a basis of linear momentum photon wave functions and of angular
momentum ones are covered. For the angular momentum wave functions,
the long wave length approximation will be made that 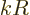 is small.
Here
is small.
Here  is the photon wave number and
is the photon wave number and  the typical size of atom or
nucleus.
the typical size of atom or
nucleus.
The derivations include a term due to an effect that was mentioned in
the initial 1952 derivation by B. Stech, [44]. This effect
is not mentioned in any textbook that the author is aware off. That
seems to be unjustified. The term does not appear to be small for
nuclei, but at the very least comparable to the usual electric
multipole element given.
The rules of engagement are as follows:
- The considered particle will be indicated by a subscript
 .
.
- The Cartesian axes are numbered using an index
 , with
, with

 1, 2, and 3 for
1, 2, and 3 for  ,
, 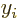 , and
, and  respectively.
respectively.
- Also,
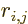 indicates the coordinate in the
indicates the coordinate in the  direction,
direction,
 ,
, 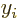 , or
, or  .
.
- Derivatives with respect to a coordinate
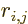 are indicated
by a simple subscript
are indicated
by a simple subscript  .
.
- If the quantity being differentiated is a vector, a comma is
used to separate the vector index from differentiation ones.
- A bare
 integral sign is assumed to be an integration over
all nuclear coordinates.
integral sign is assumed to be an integration over
all nuclear coordinates.
- A superscript
 indicates a complex conjugate.
indicates a complex conjugate.
The convoluted derivations in this note make use of a trick. Since
trick
sounds too tricky, it will be referred to as:
Lemma 1: This lemma allows you to get rid of
derivatives on the wave function. The lemma assumes nonrelativistic
particles. It is a generalization of a derivation of [16].
The lemma says that if  is the number of a particle in the atom or
nucleus, and if
is the number of a particle in the atom or
nucleus, and if 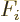 is any function of the position of that particle
is any function of the position of that particle
 , then
, then
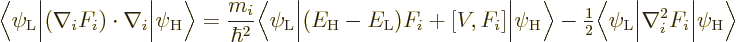 |
(D.26) |
Here  represents the vector of derivatives with respect to
the coordinates of particle
represents the vector of derivatives with respect to
the coordinates of particle  ,
,  is the potential, and
is the potential, and
 and
and  are the final and initial atomic
or nuclear wave functions.
are the final and initial atomic
or nuclear wave functions.
The energy difference can be expressed in terms of the energy
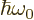 of the nominal photon emitted in the transition,
of the nominal photon emitted in the transition,
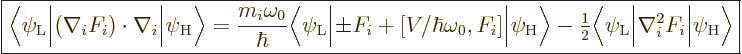 |
(D.27) |
The  allows for the possibility (in absorption) that
allows for the possibility (in absorption) that
 is actually the high energy state. The nominal photon
frequency
is actually the high energy state. The nominal photon
frequency  is normally taken equal to the actual photon
frequency
is normally taken equal to the actual photon
frequency  .
.
Note that none of my sources includes the commutator in the first
term, not even [16]. (The original 1952 derivation by
[44] used a relativistic Dirac formulation, in which the
term appears in a different place than here. The part in which it
appears there is small without the term and is not worked out with it
included.) The commutator is zero if the potential  only depends
on the position coordinates of the particles. However, nuclear
potentials include substantial momentum terms.
only depends
on the position coordinates of the particles. However, nuclear
potentials include substantial momentum terms.
To prove the lemma, start with the left hand side
where subscripts 
 1, 2, and 3 indicates the derivatives with
respect to the three coordinates of particle
1, 2, and 3 indicates the derivatives with
respect to the three coordinates of particle  . Summation
over
. Summation
over  is to be understood. Average the above expression with what
you get from doing an integration by parts:
is to be understood. Average the above expression with what
you get from doing an integration by parts:
or differentiating out
Combine the first two integrals
and do another integration by parts (I got this from [16],
thanks):
Now note the nonrelativistic eigenvalue problems for the two states
Here the sum is over the other particles in the nucleus. These two
eigenvalue problems are used to eliminate the second order derivatives
in the integral above. The terms involving the Laplacians with
respect to the coordinates of the other particles then drop out. The
reason is that 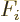 is just a constant with respect to those
coordinates, and that Laplacians are Hermitian. Assuming that
is just a constant with respect to those
coordinates, and that Laplacians are Hermitian. Assuming that  is
at least Hermitian, as it should, the
is
at least Hermitian, as it should, the  terms produce the commutator
in the lemma. And the right hand sides give the energy-difference
term. The result is the lemma as stated.
terms produce the commutator
in the lemma. And the right hand sides give the energy-difference
term. The result is the lemma as stated.
D.43.1 Matrix element for linear momentum modes
This requires in addition:
Lemma 2: This lemma allows you to express a certain
combination of derivatives in terms of the angular momentum operator.
It will be assumed that vector 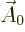 is normal to vector
is normal to vector
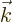 .
.
In that case:
The quickest way to prove this is to take the  -axis in the
direction of
-axis in the
direction of 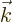 , and the
, and the  -axis in the direction of
-axis in the direction of
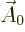 . (The expression above is also true if the two vectors
are nor orthogonal. You can see that using index notation. However,
that will not be needed.) The final equality is just the definition
of the angular momentum operator.
. (The expression above is also true if the two vectors
are nor orthogonal. You can see that using index notation. However,
that will not be needed.) The final equality is just the definition
of the angular momentum operator.
The objective is now to use these lemmas to work out the matrix element
where 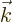 is the constant wave number vector and
is the constant wave number vector and 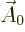 is some
other constant vector normal to
is some
other constant vector normal to 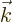 . Also
. Also  is the
position of the considered particle, and
is the
position of the considered particle, and 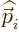 is the momentum
operator
is the momentum
operator 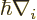

 based on these coordinates.
based on these coordinates.
To reduce this, take the factor 

 out of
out of 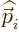 and write the
exponential in a Taylor series:
and write the
exponential in a Taylor series:
Take another messy factor out of the inner product:
For brevity, just consider the inner product by itself for now. It
can trivially be rewritten as a sum of two terms, ([16], not
me):
Now on the first inner product (1), lemma 1 can be applied with
(Recall that 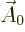 and
and 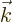 are orthogonal. Also note that the
Laplacian of
are orthogonal. Also note that the
Laplacian of 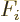 is of essentially the same form as
is of essentially the same form as 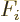 ,
just for a different value of
,
just for a different value of  .) On the second inner product
(2), lemma 2 can be applied.
.) On the second inner product
(2), lemma 2 can be applied.
Plugging these results back into the expression for the matrix
element, renotating  into
into  for the first part of (1), into
for the first part of (1), into
 for the second part, which can then be combined with the
first part, and into
for the second part, which can then be combined with the
first part, and into  for (2), and cleaning up gives the final
result:
for (2), and cleaning up gives the final
result:
where
and
Here 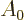 is the magnitude of
is the magnitude of 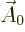 . Also
. Also 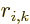 is the
component of the position
is the
component of the position  of particle
of particle  in the direction of
motion of the electromagnetic wave. The direction of motion is the
direction of
in the direction of
motion of the electromagnetic wave. The direction of motion is the
direction of 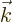 . Similarly
. Similarly  is the component of
is the component of
 in the direction of the electric field. The electric field
has the same direction as
in the direction of the electric field. The electric field
has the same direction as  . Further,
. Further, 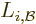 is the
component of the orbital angular momentum operator of particle
is the
component of the orbital angular momentum operator of particle  in
the direction of the magnetic field. The magnetic field is in the
same direction as
in
the direction of the magnetic field. The magnetic field is in the
same direction as 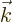

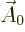 . Finally, the factor
. Finally, the factor
 is
is
The approximation applies because normally the energy release in a
transition is small compared to the rest mass energy of the particle.
(And if it was not, the nonrelativistic electromagnetic interaction
used here would not be valid in the first place.) For the emission
process covered in {A.25}, the plus sign applies, 
 1.
1.
The commutator is zero if the potential depends only on position.
That is a valid approximation for electrons in atoms, but surely not
for nuclei. For these it is a real problem, {N.14}.
For addendum {A.25}, the constant 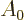 should be taken
equal to
should be taken
equal to 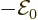

 . Note also that the
interaction of the particle spin with the magnetic field still needs
to be added to
. Note also that the
interaction of the particle spin with the magnetic field still needs
to be added to 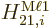 . This interaction is
unchanged from the naive approximation.
. This interaction is
unchanged from the naive approximation.
D.43.2 Matrix element for angular momentum modes
This subsection works out the details of the matrix element when
angular momentum modes are used for the photon wave function.
The first matrix element to find is
where, {A.21.7},
is the electric multipole vector potential at the location of particle
 . This uses the short hand
. This uses the short hand
where  is the multipole order or photon angular momentum,
is the multipole order or photon angular momentum,  the photon wave number,
the photon wave number, 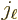 a spherical Bessel function, and
a spherical Bessel function, and
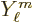 a spherical harmonic.
a spherical harmonic.
Note that the electric multipole vector potential is closely related
to the magnetic one:
The expression for the electric potential can be simplified for
long photon wave lengths. Note first that
where the second equality applied because the vector potentials are
solenoidal and the standard vector identity (D.1), while
the third equality is the energy eigenvalue problem,
{A.21}. It follows that the electric vector potential is
of the form
because vector calculus says that if the curl of something is zero, it
is the gradient of some scalar function 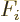 . Here
. Here
The direction of integration in the expression for 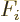 does not make
a difference, so the simplest is to integrate radially outwards. The
expression for
does not make
a difference, so the simplest is to integrate radially outwards. The
expression for 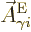 was given in
{D.36.2}. That gives
was given in
{D.36.2}. That gives
Long photon wave length corresponds to small photon wave number
 . All
. All 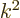 terms above can then be ignored and in addition
the following approximation for the Bessel function applies,
{A.6},
terms above can then be ignored and in addition
the following approximation for the Bessel function applies,
{A.6},
This is readily integrated to find
and 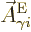 is the gradient.
is the gradient.
That allows lemma 1 to be used to find the electric matrix element.
This assumes  is indeed the lower-energy state. The
value of
is indeed the lower-energy state. The
value of 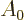 (as defined here) to use in addendum
{A.25} is
(as defined here) to use in addendum
{A.25} is
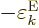

 .
.
The commutator is again negligible for atoms, but a big problem for
nuclei, {N.14}.
There is also a term due to the interaction of the spin with the
magnetic field, given by the curl of 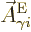 as already found above,
as already found above,
Using the property of the scalar triple product that the factors can
be interchanged if a minus sign is added, the matrix element becomes
(Note that  only acts on the
only acts on the
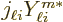 ;
; 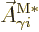 is a
function, not a differential operator.) In the long wave length
approximation of the Bessel function, that becomes
is a
function, not a differential operator.) In the long wave length
approximation of the Bessel function, that becomes
The inner product should normally be of the same order as the one of
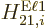 . However, the second fraction above is
normally small; usually the photon energy is small compared to the
rest mass energy of the particles. (And if it was not, the
nonrelativistic electromagnetic interaction used here would not be
valid in the first place.) So this second term will be ignored in
addendum {A.25}.
. However, the second fraction above is
normally small; usually the photon energy is small compared to the
rest mass energy of the particles. (And if it was not, the
nonrelativistic electromagnetic interaction used here would not be
valid in the first place.) So this second term will be ignored in
addendum {A.25}.
The third matrix element to find is the magnetic multipole one
Note that in index notation
where 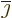 follows
follows  in the cyclic sequence
in the cyclic sequence  and
and 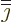 precedes
precedes  . By a trivial renotation of the
summation indices,
. By a trivial renotation of the
summation indices,
where 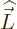 is the orbital angular momentum operator. Note that
the parenthetical term commutes with this operator, something not
mentioned in [33, p. 874].
is the orbital angular momentum operator. Note that
the parenthetical term commutes with this operator, something not
mentioned in [33, p. 874].
It follows that
or in the long wave length approximation
There is also a term due to the interaction of the spin with the
magnetic field, given by the curl of 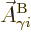 ,
which equals
,
which equals 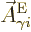 ,
,
Using the same long wave length approximation for
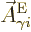 as before, that becomes
as before, that becomes
The orbital and spin matrix elements may be combined into one as
The value of 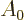 to use in addendum {A.25} is
to use in addendum {A.25} is
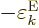

 .
.
D.43.3 Weisskopf and Moszkowski estimates
This subsection explains where the radial, angular, and momentum
factors in the Weisskopf and Moszkowski estimates come from. These
factors represent the nondimensionalized matrix elements.
The electric matrix element is simplest. It is, written out in
spherical coordinates using the assumed wave functions,
The Weisskopf and Moszkowski estimates assume that the radial parts of
wave functions equal a constant 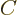 until the nuclear edge
until the nuclear edge  and are
zero outside the nucleus. To perform the radial integral is then
straightforward:
and are
zero outside the nucleus. To perform the radial integral is then
straightforward:
The first equality is true because the integral in the denominator is
1 on account of the normalization condition of wave functions. The
second inequality follows from integrating.
The angular integral above is more tricky to ballpark. First of all,
it will be assumed that the matrix element of interest is the lowest
multipole order allowed by angular momentum conservation. That seems
reasonable, given that normally higher multipole transitions will be
very much slower. It follows that 

 . (The possibility that the initial
and final angular momenta are equal will be ignored.)
. (The possibility that the initial
and final angular momenta are equal will be ignored.)
The change in orbital angular momenta could in principle be up to one
unit different from the change in net angular momenta because of the
spins. But parity conservation allows only 

 .
.
To simplify even further, assume the following specific angular
states:
which have
If these states are substituted into the angular integral, the product
of the spin states is 1 because spin states are orthonormal. What is
left is
Now 
 1
1
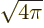 which is just a constant that can be
taken out of the integral. There it cancels the corresponding square
root in the definition of the matrix element. Then it is seen that
the transition can only create a photon for which
which is just a constant that can be
taken out of the integral. There it cancels the corresponding square
root in the definition of the matrix element. Then it is seen that
the transition can only create a photon for which 

 . The reason is that spherical harmonics are orthonormal;
the inner product is only nonzero if the two spherical harmonics are
equal, and then it is 1. So the conclusion is that for the given
states
. The reason is that spherical harmonics are orthonormal;
the inner product is only nonzero if the two spherical harmonics are
equal, and then it is 1. So the conclusion is that for the given
states
The angular integral is 1. That makes the decay rate exactly 1
Weisskopf unit.
One glaring deficiency in the above analysis was the assumption that
the initial proton state was a 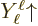 one. It would
certainly be reasonable to have an initial nuclear state that has
orbital angular momentum
one. It would
certainly be reasonable to have an initial nuclear state that has
orbital angular momentum 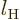

 and total angular
momentum
and total angular
momentum 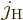

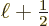 . But a bunch of
these nuclei would surely each be oriented in its own random
direction. So they would have different magnetic quantum numbers
. But a bunch of
these nuclei would surely each be oriented in its own random
direction. So they would have different magnetic quantum numbers
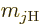 . They would not all have
. They would not all have 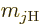

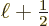 .
.
Fortunately, it turns out that this makes no difference. For example,
by symmetry the state 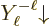 decays just as happily to
decays just as happily to
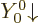 as
as 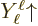 does to
does to 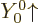 . For other
values of
. For other
values of 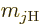 it is a bit more nuanced. They produce an
initial state of the form:
it is a bit more nuanced. They produce an
initial state of the form:
Now the first term produces decays to 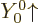 by the emission of a
photon with
by the emission of a
photon with 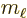

 . However, because of
the factor
. However, because of
the factor 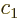 the number of such decays that occur per second is a
factor
the number of such decays that occur per second is a
factor 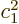 less than the Weisskopf unit. But the second term
produces decays to
less than the Weisskopf unit. But the second term
produces decays to 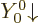 by the emission of a photon with
by the emission of a photon with
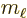

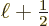 . This decay rate is a factor
. This decay rate is a factor
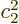 less than the Weisskopf unit. Since
less than the Weisskopf unit. Since 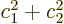
 1,
(the normalization condition of the state), the total decay rate is
still 1 Weisskopf unit.
1,
(the normalization condition of the state), the total decay rate is
still 1 Weisskopf unit.
So as long as the final state  has zero orbital angular
momentum, the decay is at 1 Weisskopf unit. The orientation of the
initial state makes no difference. That is reflected in table
A.3. This table lists the angular factors to be applied
to the Weisskopf unit to get the actual decay rate. The first row
shows that, indeed, when the final angular momentum is
has zero orbital angular
momentum, the decay is at 1 Weisskopf unit. The orientation of the
initial state makes no difference. That is reflected in table
A.3. This table lists the angular factors to be applied
to the Weisskopf unit to get the actual decay rate. The first row
shows that, indeed, when the final angular momentum is
 , as occurs for zero angular momentum, and the initial
angular momentum is
, as occurs for zero angular momentum, and the initial
angular momentum is 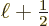 , then no correction is
needed. The correction factor is 1.
, then no correction is
needed. The correction factor is 1.
More interesting is the possibility that the two states are swapped.
Then the initial state is the one with zero orbital angular momentum.
It might at first seem that that will not make a difference either.
After all, decay rates between specific states are exactly the
same.
But there is in fact a difference. Previously, each initial nucleus
had only two states to decay to: the spin-up and the spin-down version
of the final state. Now however, each initial nucleus has
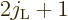 , i.e.
, i.e. 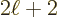 final states it can decay to,
corresponding to the possible values of the final magnetic quantum
number
final states it can decay to,
corresponding to the possible values of the final magnetic quantum
number 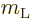 . That will increase the total decay rate
correspondingly. In fact, suppose that the initial nuclei come in
spin-up and spin-down pairs. Then each pair will decay at a rate of
one Weisskopf unit to each possible final state. That is because this
picture is the exact reverse of the decay of the final state. So the
pairs would decay at a rate
. That will increase the total decay rate
correspondingly. In fact, suppose that the initial nuclei come in
spin-up and spin-down pairs. Then each pair will decay at a rate of
one Weisskopf unit to each possible final state. That is because this
picture is the exact reverse of the decay of the final state. So the
pairs would decay at a rate 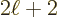 faster than the Weisskopf unit.
So by symmetry each nucleus of the pair decays
faster than the Weisskopf unit.
So by symmetry each nucleus of the pair decays  times faster
than the Weisskopf unit. That is reflected in the first column of
table A.3. (Recall that
times faster
than the Weisskopf unit. That is reflected in the first column of
table A.3. (Recall that  is the difference in the
is the difference in the
 values.)
values.)
If neither the initial nor final state has zero orbital angular
momentum, it gets more messy. Figuring out the correction factor in
that case is something for those who love abstract mathematics.
Next consider magnetic multipole transitions. They are much messier
to ballpark. It will again be assumed that the multipole order is the
smallest possible. Unfortunately, now the final orbital angular
momentum cannot be zero. Because of parity, that would require that
the initial orbital angular momentum would be  . But
that is too large because of the limitation (A.175) on the
orbital angular momentum change in magnetic transitions. Therefore
the simplest possible initial and final states have
. But
that is too large because of the limitation (A.175) on the
orbital angular momentum change in magnetic transitions. Therefore
the simplest possible initial and final states have
For these quantum numbers, the initial and final states are
where the square roots come from figure 12.5 in the
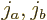

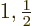 tabulation.
tabulation.
Now consider the form of the magnetic matrix element
(A.181). First note, {D.43.2}, that the
angular momentum and gradient factors commute. That helps because
then the angular momentum operators, being Hermitian, can be applied
on the easier state  .
.
The  -component part of the dot product in the matrix element is
then the easiest. The
-component part of the dot product in the matrix element is
then the easiest. The  components of the angular momentum
operators leave the state
components of the angular momentum
operators leave the state  essentially unchanged. They
merely multiply the two terms by the eigenvalue
essentially unchanged. They
merely multiply the two terms by the eigenvalue 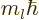 respectively
respectively 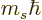 .
.
Next, this gets multiplied by the  -component of the gradient. But
multiplying by the gradient cannot change the spin. So the spin-down
first term in
-component of the gradient. But
multiplying by the gradient cannot change the spin. So the spin-down
first term in  stays spin-down. That cannot match the
spin-up of
stays spin-down. That cannot match the
spin-up of  . So the first term does not produce
a contribution.
. So the first term does not produce
a contribution.
The second term in  has the right spin. Since spin
states are orthonormal, their inner product produces 1. But now there
is a problem of matching the magnetic quantum number of
has the right spin. Since spin
states are orthonormal, their inner product produces 1. But now there
is a problem of matching the magnetic quantum number of
 . In particular, consider the harmonic
polynomial
. In particular, consider the harmonic
polynomial 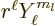 in the gradient. The gradient
reduces it to a combination of harmonic polynomials of one degree
less, in other words, to
in the gradient. The gradient
reduces it to a combination of harmonic polynomials of one degree
less, in other words, to 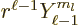 polynomials.
That limits
polynomials.
That limits  to a value no larger than
to a value no larger than  , and since
the second term in
, and since
the second term in  has magnetic quantum number 0, the
value
has magnetic quantum number 0, the
value  in
in  cannot be matched. The bottom line is
that the
cannot be matched. The bottom line is
that the  -component terms in the inner product of the matrix
element do not produce a contribution.
-component terms in the inner product of the matrix
element do not produce a contribution.
However, the  - and
- and  -component terms are another
story. The angular momentum operators in these directions change the
corresponding magnetic quantum numbers, chapter 12.11. In
general, their application produces a mixture of
-component terms are another
story. The angular momentum operators in these directions change the
corresponding magnetic quantum numbers, chapter 12.11. In
general, their application produces a mixture of 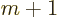 and
and  states. In particular, the
states. In particular, the  and
and  components of spin will
produce a spin-up version of the first term in
components of spin will
produce a spin-up version of the first term in  .
That now matches the spin in
.
That now matches the spin in  and a nonzero
contribution results. Similarly, the orbital angular momentum
operators will produce an
and a nonzero
contribution results. Similarly, the orbital angular momentum
operators will produce an 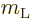
 1 version of the second
term in
1 version of the second
term in  . Combined with the
. Combined with the  units from
the gradient, that is enough to match the magnetic quantum number of
units from
the gradient, that is enough to match the magnetic quantum number of
 . So there is a total of four nonzero
contributions to the matrix element.
. So there is a total of four nonzero
contributions to the matrix element.
Now it is just a matter of working out the details to get the complete
matrix element. The information in chapter 12.11 can be used
to find the exact states produced from
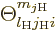 by the
by the  and
and  angular momentum operators. Each state is a multiple of the
angular momentum operators. Each state is a multiple of the
 state. As far as the gradient term is concerned, the
harmonic polynomials are of the general form
state. As far as the gradient term is concerned, the
harmonic polynomials are of the general form
as seen in table 4.3 or {D.64}. The
constants 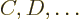 are of no importance here. The
are of no importance here. The  and
and  derivatives of the first harmonic polynomial will give the needed
derivatives of the first harmonic polynomial will give the needed
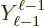 harmonic. (For values of
harmonic. (For values of  greater than 1,
the third harmonic could also make a contribution. However, it turns
out that here the
greater than 1,
the third harmonic could also make a contribution. However, it turns
out that here the  and
and  contributions cancel each other.) The
effect of the
contributions cancel each other.) The
effect of the  -derivative on the first harmonic is simply to add a
factor
-derivative on the first harmonic is simply to add a
factor 

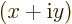 to it. Similarly, the
to it. Similarly, the  -derivative
simply adds a factor
-derivative
simply adds a factor 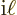

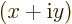 . Now if you look
up
. Now if you look
up 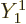 in table 4.3, you see it is a multiple of
in table 4.3, you see it is a multiple of
 . So the product with the gradient term produces a
simple multiple of
. So the product with the gradient term produces a
simple multiple of 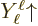 . The inner product with
. The inner product with
 then produces that multiple (which still depends on
then produces that multiple (which still depends on
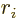 of course.) Identifying and adding the four multiples produces
of course.) Identifying and adding the four multiples produces
The remaining radial integral may be ballparked exactly the same as
for the electric case. The only difference is that the power of 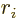 is one unit smaller.
is one unit smaller.
A similar analysis shows that the given initial state cannot decay to
the version of the final state with negative magnetic quantum number
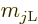

 .
.
And of course, if the initial and final states are swapped, there is
again a factor  increase in decay rate.
increase in decay rate.
More interestingly, the same expression turns out to hold if neither
the initial nor the final angular momentum equals  ,
using the correction factor of table A.3. But the
obtained magnetic multipole decay rate is more limited than the
electric one. It does require that
,
using the correction factor of table A.3. But the
obtained magnetic multipole decay rate is more limited than the
electric one. It does require that 

 and that
and that 


The momentum factors (A.189) were identified using a
computer program. This program crunched out the complete matrix
elements using procedures exactly like the ones above. This program
was also used to create table A.3 of angular factors.
This guards against typos and provides an independent check on the
Clebsch-Gordan values.
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
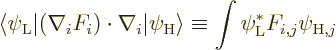
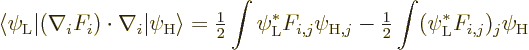
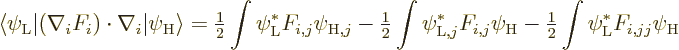

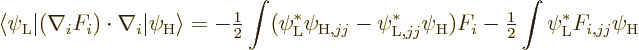

![]()
![]() .
.![]()
![]()
![]()
![]()
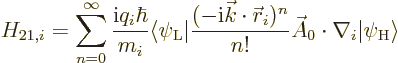

![]()
![]()
![]()
![]()
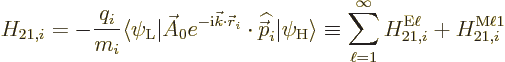
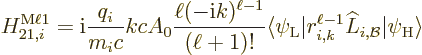
![]()
![]()
![]()
![]() .
.![]() .
.![\begin{displaymath}
F_i = \int_{{\underline{\skew0\vec r}}_i=0}^{{\skew0\vec r}...
...{m}{\skew0\vec r}_i] \cdot {\rm d}{\underline{\skew0\vec r}}_i
\end{displaymath}](img6779.gif)
![\begin{displaymath}
F_i = \int_{{\underline r}_i=0}^{r_i}[-l(l+1)+k^2r^2]j_{\ell i}\frac{{\rm d}r}r\;Y_{\ell i}^{m}
\end{displaymath}](img6781.gif)
![]() .
.![]()

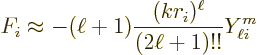
![\begin{eqnarray*}
H_{21,i}^{\rm E\ell 1} & = & - \frac{q_i}{m_i}
\langle\psi_{...
...hbar\omega,r_i^\ell Y_{\ell i}^{m*}]
\vert\psi_{\rm {H}}\rangle
\end{eqnarray*}](img6784.gif)
![]()
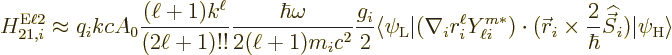
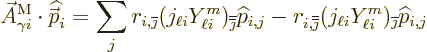
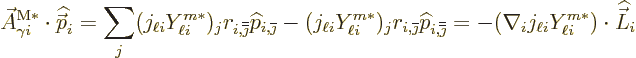
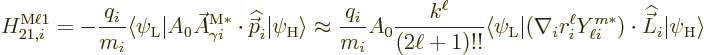
![]() ,
,![]() ,
,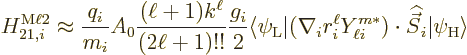
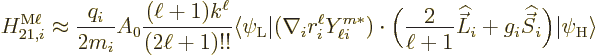
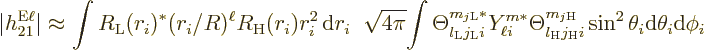
![]()
![]()
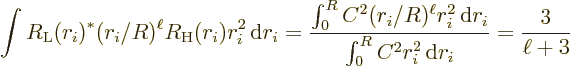
![]()
![]()
![]() .
.![]()
![]()
![]() .
.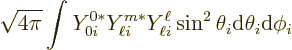
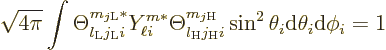
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]() .
.![]()
![]()
![]() .
.![]()
![]()
![]()
![]() .
.![]()
![]()
![]() ,
,![]() ,
,![]() ,
,![]()
![]() .
.![]()
![]()
![]()
![]()
![]() .
.
![]() .
.![]() -
-![]()
![]()
![]()
![]() .
.![]() -
-![]()
![]() .
.![]()
![]() .
.![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]() -
-![]() -
-![]() -
-![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]() .
.![]()
![]() .
.![]()
![]()
![]()
![]()
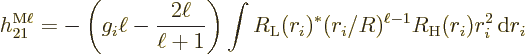
![]()
![]()
![]() .
.![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()