| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
Subsections
A.45 Fermi theory
This note needs more work, but as far as I know is basically OK.
Unfortunately, a derivation of electron capture for zero spin
transitions is not included.
This note derives the Fermi theory of beta decay. In particular, it
gives the ballparks that were used to create figure 14.54.
It also describes the Fermi integral plotted in figure
14.52, as well as Fermi’s (second) golden rule. There
is also a final subsection on electron capture, A.45.7.
When beta decay was first observed, it was believed that the nucleus
simply ejected an electron. However, problems quickly arose with
energy and momentum conservation. To solve them, Pauli proposed in
1931 that in addition to the electron, also a neutral particle was
emitted. Fermi called it the neutrino,
for
small neutral one.
Following ideas of Pauli in 1933,
Fermi in 1934 developed a comprehensive theory of beta decay. The
theory justifies the various claims made about allowed and forbidden
beta decays. It also allows predictions of the decay rate and the
probability that the electron and antineutrino will come out with
given kinetic energies. This note gives a summary. The ballparks as
described in this note are the ones used to produce figure
14.54.
A large amount of work has gone into improving the accuracy of the
Fermi theory, but it is outside the scope of this note. To get an
idea of what has been done, you might start with [23]
and work backwards. One point to keep in mind is that the derivations
below are based on expanding the electron and neutrino wave functions
into plane waves, waves of definite linear momentum. For a more
thorough treatment, it may be a better idea to expand into spherical
waves, because nuclear states have definite angular momentum. That
idea is worked out in more detail in the note on gamma decay,
{A.25}. That is news to the author. But it was supposed to be there, I
think.
A.45.1 Form of the wave function
A classical quantum treatment will not do for beta decay. To see why,
note that in a classical treatment the wave function state before the
decay is taken to be of the form
where 1 through  number the nucleons. However, the decay creates
an electron and a antineutrino out of nothing. Therefore, after the
decay the classical wave function is of the form
number the nucleons. However, the decay creates
an electron and a antineutrino out of nothing. Therefore, after the
decay the classical wave function is of the form
There is no way to describe how  could evolve into
could evolve into
 . You cannot just scribble in two more arguments into a
function somewhere half way during the evolution. That would be
voodoo mathematics. And there is also a problem with one nucleon
turning from a neutron into a proton. You should really cross out the
argument corresponding to the old neutron, and write in an argument
for the new proton.
. You cannot just scribble in two more arguments into a
function somewhere half way during the evolution. That would be
voodoo mathematics. And there is also a problem with one nucleon
turning from a neutron into a proton. You should really cross out the
argument corresponding to the old neutron, and write in an argument
for the new proton.
You might think that maybe the electron and antineutrino were always
there to begin with. But that has some major problems. A lone
neutron falls apart into a proton, an electron and an antineutrino.
So supposedly the neutron would consist of a proton, an electron, and
an antineutrino. But to confine light particles like electrons and
neutrinos to the size of a nucleon would produce huge kinetic
energies. According to the Heisenberg uncertainty relation 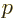


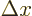 , where the energy for relativistic particles
is about
, where the energy for relativistic particles
is about 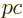 , so the kinetic energy of a light particle
confined to a 1 fm range is about 200 MeV. What conceivable force
could be strong enough to hold electrons and neutrinos that hot? And
how come the effects of this mysterious force never show up in the
atomic electrons that can be very accurately observed?
How come that electrons come out in beta decays with only a few MeV,
rather than 200 MeV?
, so the kinetic energy of a light particle
confined to a 1 fm range is about 200 MeV. What conceivable force
could be strong enough to hold electrons and neutrinos that hot? And
how come the effects of this mysterious force never show up in the
atomic electrons that can be very accurately observed?
How come that electrons come out in beta decays with only a few MeV,
rather than 200 MeV?
Further, a high-energy antineutrino can react with a proton to
create a neutron and a positron. That neutron is supposed to consist
of a proton, an electron, and an antineutrino. So, following the
same reasoning as before, the original proton before the reaction
would consist of a positron, an electron, and a proton. That
proton in turn would supposedly also consist of a positron, an
electron, and an proton. So the original proton consists of a
positron, an electron, a positron, an electron, and a proton. And so
on until a proton consists of a proton and infinitely many electron /
positron pairs. Not just one electron with very high kinetic energy
would need to be confined inside a nucleon, but an infinite number of
them, and positrons to boot. And all these electrons and positrons
would somehow have to be prevented from annihilating each other.
It just does not work. There is plenty of solid evidence that
neutrons and protons each contain three quarks, not other
nucleons along with electrons, positrons, and neutrinos. The electron
and antineutrino are created out of pure energy during beta decay, as
allowed by Einstein’s famous relativistic expression 

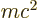 . A relativistic quantum treatment is therefore
necessary.
. A relativistic quantum treatment is therefore
necessary.
In particular, it is necessary to deal mathematically with the
appearance of the electron and an antineutrino out of nothing. To do
so, a more general, more abstract way must be used to describe the
states that nature can be in. Consider a decay that produces an
electron and an antineutrino of specific momenta 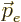 ,
respectively
,
respectively 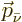 . The final state is written as
. The final state is written as
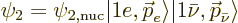 |
(A.274) |
where 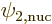 is the nuclear part of the final wave
function. The electron ket
is the nuclear part of the final wave
function. The electron ket 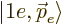 is a “Fock-space
ket,” and should be read as “one electron in the state
with angular momentum
is a “Fock-space
ket,” and should be read as “one electron in the state
with angular momentum 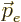 .” The antineutrino ket
should be read as “one antineutrino in the state with angular
momentum
.” The antineutrino ket
should be read as “one antineutrino in the state with angular
momentum 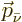 .”
.”
Similarly, the state before the decay is written as
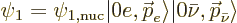 |
(A.275) |
where 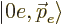 means “zero electrons in the state with
angular momentum
means “zero electrons in the state with
angular momentum 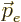 ,” and similar for the
antineutrino ket. Written in this way, the initial and final wave
functions are no longer inconsistent. What is different is not the
form of the wave function, but merely how many electrons and
antineutrinos are in the states with momentum
,” and similar for the
antineutrino ket. Written in this way, the initial and final wave
functions are no longer inconsistent. What is different is not the
form of the wave function, but merely how many electrons and
antineutrinos are in the states with momentum 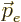 ,
respectively
,
respectively 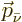 . Before the decay, the “occupation numbers” of these states are zero electrons and zero
antineutrinos. After the decay, the occupation numbers are one
electron and one neutrino. It is not that the initial state does not
have occupation numbers for these states, (which would make
. Before the decay, the “occupation numbers” of these states are zero electrons and zero
antineutrinos. After the decay, the occupation numbers are one
electron and one neutrino. It is not that the initial state does not
have occupation numbers for these states, (which would make
 and
and  inconsistent), but merely that these occupation
numbers have the value zero, (which does not).
inconsistent), but merely that these occupation
numbers have the value zero, (which does not).
(You could also add kets for different momentum states that the final
electron and antineutrino are not in after the decay. But
states that have zero electrons and neutrinos both before and after
the considered decay are physically irrelevant and can be left away.)
That leaves the nuclear part of the wave function. You could use
Fock-space kets to deal with the disappearance of a neutron and
appearance of a proton during the decay. However, there is a neater
way. The total number of nucleons remains the same during the decay.
The only thing that happens is that a nucleon changes type from a
neutron into a proton. The mathematical trick is therefore to take the
particles to be nucleons, instead of protons and neutrons. If you
give each nucleon a nucleon type
property, then the
only thing that happens during the decay is that the nucleon type of
one of the nucleons flips over from neutron to proton. No nucleons
are created or destroyed. Nucleon type is typically indicated by the
symbol 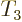 and is defined to be
and is defined to be 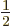 if the nucleon is
a proton and
if the nucleon is
a proton and  if the nucleon is a neutron. (Some older
references may define it the other way around.) The general form of
the nuclear wave function therefore becomes
if the nucleon is a neutron. (Some older
references may define it the other way around.) The general form of
the nuclear wave function therefore becomes
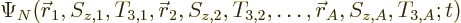
During the decay, the 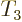 value of one nucleon will change from
value of one nucleon will change from
 to
to 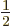 .
.
Of course, the name nucleon type
for 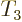 is not
really acceptable, because it is understandable. In the old days, the
names
is not
really acceptable, because it is understandable. In the old days, the
names isobaric spin” or “isotopic spin
were used, because nucleon type has absolutely nothing to do with
spin. However, it was felt that these nonsensical names could cause
some smart outsiders to suspect that the quantity being talked about
was not really spin. Therefore the modern term isospin
was introduced. This term contains nothing to give the secret away
that it is not spin at all.
A.45.2 Source of the decay
Next the source of the decay must be identified. Ultimately that must
be the Hamiltonian, because the Hamiltonian describes the time
evolution of systems according to the Schrödinger equation.
In a specific beta decay process, two states are involved. A state
 describes the nucleus before the decay, and a state
describes the nucleus before the decay, and a state  describes the combination of nucleus, electron, and antineutrino after
the decay. That makes the system into a so-called “two state
system.” The unsteady evolution of such systems was discussed
in chapter 7.6 and {D.38}. The key to the
solution were the
describes the combination of nucleus, electron, and antineutrino after
the decay. That makes the system into a so-called “two state
system.” The unsteady evolution of such systems was discussed
in chapter 7.6 and {D.38}. The key to the
solution were the Hamiltonian coefficients.
The first
one is:
where 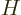 is the (relativistic) Hamiltonian. The value of
is the (relativistic) Hamiltonian. The value of 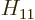 is
the expectation value of the energy
is
the expectation value of the energy 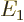 when nature is in the state
when nature is in the state
 . Assuming that the nucleus is initially at rest, the
relativistic energy is just the rest mass energy of the nucleus. It
is given in terms of its mass by Einstein’s famous relation
. Assuming that the nucleus is initially at rest, the
relativistic energy is just the rest mass energy of the nucleus. It
is given in terms of its mass by Einstein’s famous relation 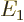

 .
.
The Hamiltonian coefficient for the final state is similarly
Using the form given in the previous section for the final wave
function, that becomes
It is the expectation value of energy after the decay. It consists of
the sum of the rest mass energies of final nucleus, electron, and
antineutrino, as well as their kinetic energies.
The Hamiltonian coefficient that describes the interaction between the
two states is crucial, because it is the one that causes the decay.
It is
Using the form for the wave functions given in the previous section:
If 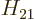 is zero, no decay will occur. And most of the Hamiltonian
does not produce a contribution to
is zero, no decay will occur. And most of the Hamiltonian
does not produce a contribution to 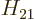 . But there is a
small part of the Hamiltonian, call it
. But there is a
small part of the Hamiltonian, call it 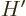 , that does produce a
nonzero interaction. That part is due to the weak force.
, that does produce a
nonzero interaction. That part is due to the weak force.
Unfortunately, Fermi had no clue what 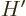 was. He assumed that beta
decay would not be that much different from the better understood
decay of excited atomic states in atoms. Gamma decay is the direct
equivalent of atomic decay for excited nuclei. Beta decay is
definitely different, but maybe not that different. In atomic decay
an electromagnetic photon is created, rather than an electron and
antineutrino. Still the general idea seemed similar.
was. He assumed that beta
decay would not be that much different from the better understood
decay of excited atomic states in atoms. Gamma decay is the direct
equivalent of atomic decay for excited nuclei. Beta decay is
definitely different, but maybe not that different. In atomic decay
an electromagnetic photon is created, rather than an electron and
antineutrino. Still the general idea seemed similar.
In atomic decay 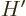 is essentially proportional to the product of the
charge of the excited electron, times the spatial eigenstate of the
photon, times a
is essentially proportional to the product of the
charge of the excited electron, times the spatial eigenstate of the
photon, times a photon creation
operator 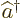 :
:

In words, it says that the interaction of the electron with the
electromagnetic field can create photons. The magnitude of that
effect is proportional to the amplitude of the photon at the location
of the electron, and also to the electric charge of the electron. The
electric charge acts as a “coupling constant” that links electrons and photons together.
If the electron was uncharged, it would not be able to create photons.
So it would not be able to create an electric field. Further, the
fact that the coupling between the electron and the photon occurs at
the location of the electron eliminates some problems that relativity
has with action at a distance.
There is another term in 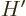 that involves an annihilation operator
that involves an annihilation operator
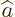 instead of a creation operator. An annihilation operator
destroys photons. However, that does not produce a contribution to
instead of a creation operator. An annihilation operator
destroys photons. However, that does not produce a contribution to
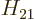 ; if you try to annihilate the nonexisting photon in the
initial wave function, you get a zero wave function. On the other
hand for the earlier term, the creation operator is essential. It
turns the initial state with no photon into a state with one photon.
States with different numbers of particles are orthogonal, so the
Hamiltonian coefficient
; if you try to annihilate the nonexisting photon in the
initial wave function, you get a zero wave function. On the other
hand for the earlier term, the creation operator is essential. It
turns the initial state with no photon into a state with one photon.
States with different numbers of particles are orthogonal, so the
Hamiltonian coefficient 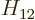 would be zero without the creation
operator. Looked at the other way around, the presence of the
creation operator in the Hamiltonian ensures that the final state must
have one more photon for the decay to occur. (See addendum
{A.15} for more details on electromagnetic interactions,
including a more precise description of
would be zero without the creation
operator. Looked at the other way around, the presence of the
creation operator in the Hamiltonian ensures that the final state must
have one more photon for the decay to occur. (See addendum
{A.15} for more details on electromagnetic interactions,
including a more precise description of 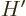 . See also
{A.25}.)
. See also
{A.25}.)
Fermi assumed that the general ideas of atomic decay would also hold
for beta decay of nuclei. Electron and antineutrino creation
operators in the Hamiltonian would turn the zero-electron and
zero-antineutrino kets into one-electron and one-antineutrino ones.
Then the inner products of the kets are equal to one pairwise.
Therefore both the creation operators and the kets drop out of the
final expression. In that way the Hamiltonian coefficient simplifies
to
where the index  is the nucleon number and
is the nucleon number and 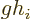 is the remaining
still unknown part of the Hamiltonian. In indicating this unknown
part by
is the remaining
still unknown part of the Hamiltonian. In indicating this unknown
part by 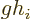 , the assumption is that it will be possible to
write it as some generic dimensional constant
, the assumption is that it will be possible to
write it as some generic dimensional constant  times some simple
nondimensional operator
times some simple
nondimensional operator 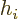 acting on nucleon number
acting on nucleon number  .
.
To write expressions for the wave functions of the electron and
antineutrino, you face the complication that unbound states in
infinite space are not normalizable. That produced mathematical
complications for momentum eigenstates in chapter 7.9.2,
and similar difficulties resurface here. To simplify things, the
mathematical trick is to assume that the decaying nucleus is not in
infinite space, but in an extremely large “periodic
box.” The assumption is that nature repeats itself spatially; a
particle that exits the box through one side reenters it through the
opposite side. Space wraps around
if you want, and
opposite sides of the box are assumed to be physically the same
location. It is like on the surface of the earth: if you move along
the straightest-possible path on the surface of the earth, you travel
around the earth along a big circle and return to the same point that
you started out at. Still, on a local scale, the surface on the earth
looks flat. The idea is that the empty space around the decaying
nucleus has a similar property, in each of the three Cartesian
dimensions. This trick is also commonly used in solid mechanics,
chapter 10.
In a periodic box, the wave function of the antineutrino is
where 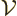 is the volume of the periodic box. It is easy to check
that this wave function is indeed normalized. Also, it is seen that
it is indeed an eigenfunction of the
is the volume of the periodic box. It is easy to check
that this wave function is indeed normalized. Also, it is seen that
it is indeed an eigenfunction of the  -momentum operator
-momentum operator


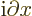 with eigenvalue
with eigenvalue 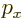 , and
similar for the
, and
similar for the  - and
- and  -momentum operators.
-momentum operators.
The wave function of the electron will be written in a similar way:
This however has an additional problem. It works fine far from the
nucleus, where the momentum of the electron is by definition the
constant vector 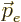 . However, near the nucleus the Coulomb
field of the nucleus, and to some extent that of the atomic electrons,
affects the kinetic energy of the electron, and hence its
momentum. Therefore, the energy eigenfunction that has momentum
. However, near the nucleus the Coulomb
field of the nucleus, and to some extent that of the atomic electrons,
affects the kinetic energy of the electron, and hence its
momentum. Therefore, the energy eigenfunction that has momentum 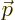 far from the nucleus differs significantly from the above exponential
closer to the nucleus. And this wave function must be evaluated at
nucleon positions inside the nucleus! The problem is particularly
large when the momentum
far from the nucleus differs significantly from the above exponential
closer to the nucleus. And this wave function must be evaluated at
nucleon positions inside the nucleus! The problem is particularly
large when the momentum 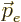 is low, because then the electron has
little kinetic energy and the Coulomb potential is relatively speaking
more important. The problem gets even worse for low-energy positron
emission, because a positively-charged positron is repelled by the
positive nucleus and must tunnel through to reach it.
is low, because then the electron has
little kinetic energy and the Coulomb potential is relatively speaking
more important. The problem gets even worse for low-energy positron
emission, because a positively-charged positron is repelled by the
positive nucleus and must tunnel through to reach it.
The usual way to deal with the problem is to stick with the
exponential electron wave function for now, and fix up the problem
later in the final results. The fix-up will be achieved by throwing
in an additional fudge factor. While “Fermi fudge
factor” alliterates nicely, it does not sound very respectful,
so physicists call the factor the Fermi function.
The bottom line is that for now
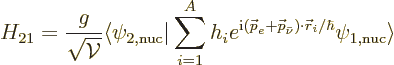 |
(A.276) |
That leaves the still unknown operator 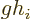 . The constant
. The constant  is simply defined so that the operator
is simply defined so that the operator 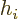 has a magnitude
that is of order one. That means that
has a magnitude
that is of order one. That means that
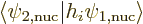 should never be
greater than about one, though it could be much less if
should never be
greater than about one, though it could be much less if
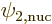 and
and 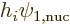 turn out to be almost
orthogonal. It is found that
turn out to be almost
orthogonal. It is found that  has a rough value of about 100 eV
fm
has a rough value of about 100 eV
fm , depending a bit on whether it is a Fermi or Gamow-Teller
decay. Figure 14.54 simply used 100 MeV fm
, depending a bit on whether it is a Fermi or Gamow-Teller
decay. Figure 14.54 simply used 100 MeV fm .
.
A.45.3 Allowed or forbidden
The question of allowed and forbidden decays is directly related to
the Hamiltonian coefficient 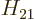 , (A.276), derived
in the previous subsection, that causes the decay.
, (A.276), derived
in the previous subsection, that causes the decay.
First note that the emitted electron and antineutrino have quite
small momentum values, on a nuclear scale. In particular,
in their combined wave function
the argument of the exponential is small. Typically, its magnitude is
only a few percent, It is therefore possible to approximate the
exponential by one, or more generally by a Taylor series:
Since the first term in the Taylor series is by far the largest, you
would expect that the value of 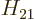 , (A.276), can
be well approximated by replacing the exponential by 1, giving:
, (A.276), can
be well approximated by replacing the exponential by 1, giving:
However, clearly this approximation does not work if the value of
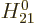 is zero for some reason:
is zero for some reason:
If the simplified coefficient 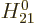 is nonzero, the decay is
allowed. If it is zero, the decay is forbidden.
is nonzero, the decay is
allowed. If it is zero, the decay is forbidden.
If the decay is forbidden, higher order terms in the Taylor series
will have to be used to come up with a nonzero value for
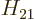 . Since these higher order terms are much smaller, and
. Since these higher order terms are much smaller, and
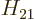 drives the decay, a forbidden decay will proceed much slower
than an allowed one.
drives the decay, a forbidden decay will proceed much slower
than an allowed one.
Why would a decay not be allowed? In other words why would
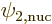 and
and 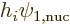 be exactly
orthogonal? If you took two random wave functions for
be exactly
orthogonal? If you took two random wave functions for
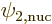 and
and 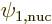 , they definitely
would not be. But
, they definitely
would not be. But 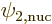 and
and 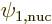 are not
random wave functions. They satisfy a significant amount of symmetry
constraints.
are not
random wave functions. They satisfy a significant amount of symmetry
constraints.
One very important one is symmetry with respect to coordinate system
orientation. An inner product of two wave functions is independent of
the angular orientation of the coordinate system in which you evaluate
it. Therefore, you can average the inner product over all directions
of the coordinate system. However, the angular variation of a wave
function is related to its angular momentum; see chapter
7.3 and its note. In particular, if you average a wave
function of definite angular momentum over all coordinate system
orientations, you get zero unless the angular momentum is zero. So,
if it was just 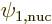 in the inner product in
in the inner product in
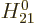 , the inner product would be zero unless the initial
nucleus had zero spin. However, the final state is also in the inner
product, and being at the other side of it, its angular variation acts
to counteract that of the initial nucleus. Therefore,
, the inner product would be zero unless the initial
nucleus had zero spin. However, the final state is also in the inner
product, and being at the other side of it, its angular variation acts
to counteract that of the initial nucleus. Therefore, 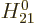 will
be zero unless the initial angular momentum is exactly balanced by the
net final angular momentum. And that is angular momentum
conservation. The decay has to satisfy it.
will
be zero unless the initial angular momentum is exactly balanced by the
net final angular momentum. And that is angular momentum
conservation. The decay has to satisfy it.
Note that the linear momenta of the electron and antineutrino have
become ignored in 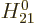 . Therefore, their orbital angular
momentum is approximated to be zero too. Under these condition
. Therefore, their orbital angular
momentum is approximated to be zero too. Under these condition
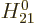 is zero unless the angular momentum of the final nucleus
plus the spin angular momentum of electron and antineutrino equals the
angular momentum of the original nucleus. Since the electron and
antineutrino can have up to one unit of combined spin, the nuclear
spin cannot change more than one unit. That is the first selection
rule for allowed decays given in chapter 14.19.6.
is zero unless the angular momentum of the final nucleus
plus the spin angular momentum of electron and antineutrino equals the
angular momentum of the original nucleus. Since the electron and
antineutrino can have up to one unit of combined spin, the nuclear
spin cannot change more than one unit. That is the first selection
rule for allowed decays given in chapter 14.19.6.
Another important constraint is symmetry under the parity
transformation 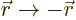 . This transformation too does not
affect inner products, so you can average the values before and after
the transform. However, a wave function that has odd parity changes
sign under the transform and averages to zero. So the inner product
in
. This transformation too does not
affect inner products, so you can average the values before and after
the transform. However, a wave function that has odd parity changes
sign under the transform and averages to zero. So the inner product
in 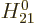 is zero if the total integrand has odd parity. For a
nonzero value, the integrand must have even parity, and that means
that the parity of the initial nucleus must equal the combined parity
of the final nucleus electron, and antineutrino.
is zero if the total integrand has odd parity. For a
nonzero value, the integrand must have even parity, and that means
that the parity of the initial nucleus must equal the combined parity
of the final nucleus electron, and antineutrino.
Since the electron and antineutrino come out without orbital angular
momentum, they have even parity. So the nuclear parity must remain
unchanged under the transition. (To be sure, this is not absolutely
justified. Nuclear wave functions actually have a tiny uncertainty in
parity because the weak force does not conserve parity, chapter
14.19.8. This effect is usually too small to be observed and
will be ignored here.)
So what if either one of these selection rules is violated? In that
case, maybe the second term in the Taylor series for the electron and
antineutrino wave functions produces something nonzero that can drive
the decay. For that to be true,
has to be nonzero. If it is, the decay is a first-forbidden one. Now
the spherical harmonics 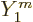 of orbital angular momentum are of the
generic form, {D.14}
of orbital angular momentum are of the
generic form, {D.14}
with the 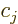 some constants. Therefore, the factor
some constants. Therefore, the factor  in
in
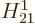 brings in angular variation corresponding to one unit of
angular momentum. That means that the total spin can now change by up
to one unit, and therefore the nuclear spin by up to two units. That
is indeed the selection rule for first forbidden decays.
brings in angular variation corresponding to one unit of
angular momentum. That means that the total spin can now change by up
to one unit, and therefore the nuclear spin by up to two units. That
is indeed the selection rule for first forbidden decays.
And note that because  changes sign when every
changes sign when every  is
replaced by
is
replaced by 
 , the initial and final nuclear parities must
now be opposite for
, the initial and final nuclear parities must
now be opposite for 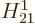 not to be zero. That is indeed the
parity selection rule for first-forbidden decays.
not to be zero. That is indeed the
parity selection rule for first-forbidden decays.
The higher order forbidden decays go the same way. For an
 th-forbidden decay,
th-forbidden decay,
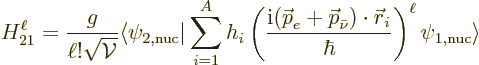 |
(A.277) |
must be the first nonzero inner product. Note that an
 th-forbidden decay has a coefficient
th-forbidden decay has a coefficient 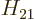 proportional to a
factor of order
proportional to a
factor of order  , with
, with  the nuclear radius.
Since the decay rate turns out to be proportional to
the nuclear radius.
Since the decay rate turns out to be proportional to
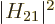 , an
, an  th-forbidden decay is slowed down by a
factor of order
th-forbidden decay is slowed down by a
factor of order  , making highly forbidden
decays extremely slow.
, making highly forbidden
decays extremely slow.
A.45.4 The nuclear operator
This subsection will have a closer look at the nuclear operator
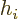 . While the discussion will be kept simple, having some
idea about the nature of this operator can be useful. It can help to
understand why some decays have relatively low decay rates that are
not explained by just looking at the electron and antineutrino wave
functions, and the nuclear spins and parities. The discussion will
mainly focus on allowed decays.
. While the discussion will be kept simple, having some
idea about the nature of this operator can be useful. It can help to
understand why some decays have relatively low decay rates that are
not explained by just looking at the electron and antineutrino wave
functions, and the nuclear spins and parities. The discussion will
mainly focus on allowed decays.
Although Fermi did not know what 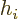 was, Pauli had already
established the possible generic forms for it allowed by relativity.
It could take the form of a scalar (S), a vector (V), an axial vector
(A, a vector like angular momentum, one that inverts when the physics
is seen in a mirror), a pseudoscalar (P, a scalar like the scalar
triple product of vectors that changes sign when the physics is seen
in the mirror), or a tensor (T, a multiple-index object like a matrix
that transforms in specific ways.) Fermi simply assumed the
interaction was of the vector, V, type in analogy with the decay of
excited atoms.
was, Pauli had already
established the possible generic forms for it allowed by relativity.
It could take the form of a scalar (S), a vector (V), an axial vector
(A, a vector like angular momentum, one that inverts when the physics
is seen in a mirror), a pseudoscalar (P, a scalar like the scalar
triple product of vectors that changes sign when the physics is seen
in the mirror), or a tensor (T, a multiple-index object like a matrix
that transforms in specific ways.) Fermi simply assumed the
interaction was of the vector, V, type in analogy with the decay of
excited atoms.
Fermi ignored the spin of the electron and antineutrino. However,
Gamow & Teller soon established that to allow for decays where
the two come out with spin, (Gamow-Teller decays), 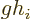 also
should have terms with axial, A, and/or tensor, T, character. Work of
Fierz combined with experimental evidence showed that the Hamiltonian
could not have both S and V, nor both A and T terms. Additional
evidence narrowed
also
should have terms with axial, A, and/or tensor, T, character. Work of
Fierz combined with experimental evidence showed that the Hamiltonian
could not have both S and V, nor both A and T terms. Additional
evidence narrowed 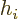 down to STP combinations or VA ones.
down to STP combinations or VA ones.
Finally, it was established in 1953 that the correct one was the STP
combination, because experimental evidence on RaE, (some physicists
cannot spell bismuth-210), showed that P was present. Unfortunately,
it did not. For one, the conclusion depended to an insane degree on
the accuracy of a correction term.
However, in 1955 it was established that it was STP anyway, because
experimental evidence on helium-6 clearly showed that the Gamow-Teller
part of the decay was tensor. The question was therefore solved
satisfactorily. It was STP, or maybe just ST. Experimental evidence
had redeemed itself.
However, in 1958, a quarter century after Fermi, it was found that
beta decay violated parity conservation, chapter 14.19.8,
and theoretically that was not really consistent with STP. So
experimentalists had another look at their evidence and quickly came
back with good news: “The helium-6 evidence does not show
Gamow-Teller is tensor after all.”
The final answer is that 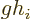 is VA. Since so much of our knowledge
about nuclei depends on experimental data, it may be worthwhile to
keep this cautionary tale, taken from the Stanford Encyclopedia of
Philosophy, in mind.
is VA. Since so much of our knowledge
about nuclei depends on experimental data, it may be worthwhile to
keep this cautionary tale, taken from the Stanford Encyclopedia of
Philosophy, in mind.
It may next be noted that 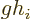 will need to include a isospin
creation operator to be able to turn a neutron into a proton. In
Fermi decays,
will need to include a isospin
creation operator to be able to turn a neutron into a proton. In
Fermi decays, 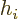 is assumed to be just that operator. The constant
of proportionality
is assumed to be just that operator. The constant
of proportionality  , usually called the coupling constant
, usually called the coupling constant
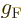 , describes the strength of the weak interaction.
That is much like the unit electric charge
, describes the strength of the weak interaction.
That is much like the unit electric charge 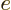 describes the strength
of the electromagnetic interaction between charged particles and
photons. In Fermi decays it is found that
describes the strength
of the electromagnetic interaction between charged particles and
photons. In Fermi decays it is found that 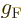 is about 88 eV
fm
is about 88 eV
fm . Note that this is quite small compared to the MeV scale
of nuclear forces. If you ballpark relative strengths of forces,
[31, p. 285] the nuclear force is strongest, the
electromagnetic force about hundred times smaller, the weak force
another thousand times smaller than that, and finally gravity is
another 10
. Note that this is quite small compared to the MeV scale
of nuclear forces. If you ballpark relative strengths of forces,
[31, p. 285] the nuclear force is strongest, the
electromagnetic force about hundred times smaller, the weak force
another thousand times smaller than that, and finally gravity is
another 10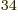 times smaller than that. The decay rates turn
out to be proportional to the square of the interaction, magnifying
the relative differences.
times smaller than that. The decay rates turn
out to be proportional to the square of the interaction, magnifying
the relative differences.
In Gamow-Teller decays, 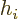 is assumed to consist of products of
isospin creation operators times spin creation or annihilation
operators. The latter operators allow the spin of the neutron that
converts to the proton to flip over. Suitable spin creation and
annihilation operators are given by the so-called “Pauli spin
matrices,” chapter 12.10 When they act on a nucleon,
they produce states with the spin in an orthogonal direction flipped
over. That allows the net spin of the nucleus to change by one unit.
The appropriate constant of proportionality
is assumed to consist of products of
isospin creation operators times spin creation or annihilation
operators. The latter operators allow the spin of the neutron that
converts to the proton to flip over. Suitable spin creation and
annihilation operators are given by the so-called “Pauli spin
matrices,” chapter 12.10 When they act on a nucleon,
they produce states with the spin in an orthogonal direction flipped
over. That allows the net spin of the nucleus to change by one unit.
The appropriate constant of proportionality 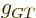 is found to be a
bit larger than the Fermi one.
is found to be a
bit larger than the Fermi one.
The relevant operators then become, [5],
for Fermi and Gamow-Teller decays respectively. Here the three
 are the Pauli spin matrices of chapter 12.10. The
are the Pauli spin matrices of chapter 12.10. The
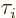 are the equivalents of the Pauli spin matrices for isospin;
in the combinations shown above they turn neutrons into protons, or
vice-versa. Please excuse: using the clarity now made possible by
modern physical terminology, they create, respectively annihilate,
isospin. The upper sign is relevant for beta-minus decay and the
lower for beta-plus decay. The Gamow-Teller operator absorbs the spin
part of the electron and antineutrino wave functions, in particular
the averaging over the directions of their spin.
are the equivalents of the Pauli spin matrices for isospin;
in the combinations shown above they turn neutrons into protons, or
vice-versa. Please excuse: using the clarity now made possible by
modern physical terminology, they create, respectively annihilate,
isospin. The upper sign is relevant for beta-minus decay and the
lower for beta-plus decay. The Gamow-Teller operator absorbs the spin
part of the electron and antineutrino wave functions, in particular
the averaging over the directions of their spin.
So how do these nuclear operators affect the decay rate? That is best
understood by going back to the more physical shell-model picture. In
beta minus decay, a neutron is turned into a proton. That proton
usually occupies a different spatial state in the proton shells than
the original neutron in the neutron shells. And different spatial
states are supposedly orthogonal, so the inner product
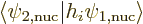 will usually be
pretty small, if the decay is allowed at all. There is one big
exception, though: mirror nuclei. In a decay between mirror nuclei, a
nucleus with a neutron number
will usually be
pretty small, if the decay is allowed at all. There is one big
exception, though: mirror nuclei. In a decay between mirror nuclei, a
nucleus with a neutron number 

 decays into one
with neutron number
decays into one
with neutron number 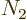

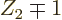 . In that case, the
nucleon that changes type remains in the same spatial orbit.
Therefore, the Fermi inner product equals one, and the Gamow Teller
one is maximal too. Allowed decays of this type are called “superallowed.” The simplest example is the beta decay of a free
neutron.
. In that case, the
nucleon that changes type remains in the same spatial orbit.
Therefore, the Fermi inner product equals one, and the Gamow Teller
one is maximal too. Allowed decays of this type are called “superallowed.” The simplest example is the beta decay of a free
neutron.
If you allow for beta decay to excited states, more superallowed
decays are possible. States that differ merely in nucleon type are
called isobaric analog states, or isospin multiplets, chapter
14.18. There are about twenty such superallowed decays in
which the initial and final nuclei both have spin zero and positive
parity. These twenty are particularly interesting theoretically,
because only Fermi decays are possible for them. And the Fermi inner
product is 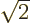 . (The reason that it is
. (The reason that it is 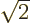 instead of 1 like for mirror nuclei can be seen from thinking of
isospin as if it is just normal spin. Mirror nuclei have an odd
number of nucleons, so the net nuclear isospin is half integer. In
particular the net isospin will be
instead of 1 like for mirror nuclei can be seen from thinking of
isospin as if it is just normal spin. Mirror nuclei have an odd
number of nucleons, so the net nuclear isospin is half integer. In
particular the net isospin will be 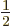 in the ground state.
However, nuclei with zero spin have an even number of nucleons, hence
integer net isospin. The isospin of the twenty decays is one; it
cannot be zero because at least one nucleus must have a nonzero net
nucleon type
in the ground state.
However, nuclei with zero spin have an even number of nucleons, hence
integer net isospin. The isospin of the twenty decays is one; it
cannot be zero because at least one nucleus must have a nonzero net
nucleon type 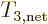 . The net nucleon type is only
zero if the number of protons is the same as the number of neutrons.
It is then seen from (12.9) and (12.10) in chapter
12 that the isospin creation or annihilation operators
will produce a factor
. The net nucleon type is only
zero if the number of protons is the same as the number of neutrons.
It is then seen from (12.9) and (12.10) in chapter
12 that the isospin creation or annihilation operators
will produce a factor 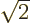 .)
.)
These decays therefore allow the value of the Fermi coupling constant
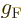 to be determined from the decay rates. It turns out to be about
88 eV fm
to be determined from the decay rates. It turns out to be about
88 eV fm , regardless of the particular decay used to compute it.
That seems to suggest that the interaction with neighboring nucleons
in a nucleus does not affect the Fermi decay process. Indeed, if the
value of
, regardless of the particular decay used to compute it.
That seems to suggest that the interaction with neighboring nucleons
in a nucleus does not affect the Fermi decay process. Indeed, if the
value of 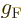 is used to analyze the decay rates of the mirror
nuclei, including the free neutron that has no neighbors, the data
show no such effect. The hypothesis that neighboring nucleons do not
affect the Fermi decay process is known as the “conserved vector current hypothesis.” What name could be
clearer than that? Unlike Fermi decays, Gamow-Teller decays are
somewhat affected by the presence of neighboring nuclei.
is used to analyze the decay rates of the mirror
nuclei, including the free neutron that has no neighbors, the data
show no such effect. The hypothesis that neighboring nucleons do not
affect the Fermi decay process is known as the “conserved vector current hypothesis.” What name could be
clearer than that? Unlike Fermi decays, Gamow-Teller decays are
somewhat affected by the presence of neighboring nuclei.
Besides the spin and parity rules already mentioned, Fermi decays must
satisfy the approximate selection rule that the magnitude of isospin
must be unchanged. They can be slowed down by several orders of
magnitude if that rule is violated.
Gamow-Teller decays are much less confined than Fermi ones because of
the presence of the electron spin operator. As the shell model shows,
nucleon spins are uncertain in energy eigenstates. Therefore, the
nuclear symmetry constraints are a lot less restrictive.
A.45.5 Fermi’s golden rule
The previous four subsections have focussed on finding the Hamiltonian
coefficients of the decay from a state  to a state
to a state
 . Most of the attention was on the coefficient
. Most of the attention was on the coefficient
 that drives the decay. The next step is solution of the
Schrödinger equation to find the evolution of the decay process.
that drives the decay. The next step is solution of the
Schrödinger equation to find the evolution of the decay process.
The quantum amplitude of the pre-decay state  will be
indicated by
will be
indicated by 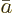 and the quantum amplitude of the final decayed
state
and the quantum amplitude of the final decayed
state  by
by 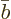 . The Schrödinger equation implies that
. The Schrödinger equation implies that
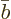 increases from zero according to
increases from zero according to
(To use this expression, the quantum amplitudes must include an
additional phase factor, but it is of no consequence for the
probability of the states. See chapter 7.6 and
{D.38} for details.)
Now picture the following. At the initial time there are a large
number of pre-decay nuclei, all with 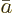
 1. All these nuclei
then evolve according to the Schrödinger equation, above, over a
time interval
1. All these nuclei
then evolve according to the Schrödinger equation, above, over a
time interval 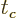 that is short enough that
that is short enough that 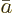 stays close to
one. (Because the perturbation of the nucleus by the weak force is
small, the magnitudes of the coefficients only change slowly on the
relevant time scale.) In that case,
stays close to
one. (Because the perturbation of the nucleus by the weak force is
small, the magnitudes of the coefficients only change slowly on the
relevant time scale.) In that case, 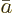 can be dropped from the
equation and its solution is then seen to be
can be dropped from the
equation and its solution is then seen to be
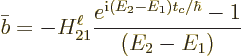
Half of the exponential can be factored out to produce a real ratio:
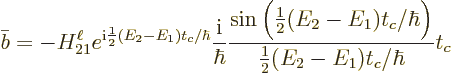
Then at the final time 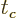 , assume that the state of all the
nuclei is
, assume that the state of all the
nuclei is measured.
The macroscopic surroundings of
the nuclei establishes whether or not electron and antineutrino pairs
have come out. The probability that a give nucleus has emitted such a
pair is given by the square magnitude 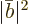 of the amplitude
of the decayed state. Therefore, a fraction
of the amplitude
of the decayed state. Therefore, a fraction 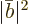 of the
nuclei will be found to have decayed and
of the
nuclei will be found to have decayed and 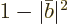 will be found
to be still in the pre-decay state
will be found
to be still in the pre-decay state  . After this
. After this
measurement,
the entire process then repeats for the
remaining 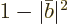 nuclei that did not decay.
nuclei that did not decay.
The bottom line is however that a fraction 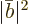 did.
Therefore, the ratio
did.
Therefore, the ratio 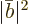

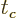 gives the specific decay rate,
the relative amount of nuclei that decay per unit time. Plugging in
the above expression for
gives the specific decay rate,
the relative amount of nuclei that decay per unit time. Plugging in
the above expression for 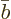 gives:
gives:
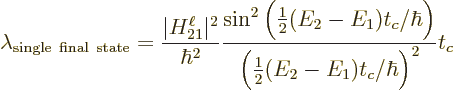 |
(A.278) |
To get the total decay rate, you must still sum over all possible
final states. Most importantly, you need to sum the specific decay
rates together for all possible electron and antineutrino momenta.
And there may be more. If the final nuclear state has spin you also
need to sum over all values of the magnetic quantum number of the
final state. (The amount of nuclear decay should not depend on the
angular orientation of the initial nucleus in empty space. However,
if you expand the electron and neutrino wave functions into spherical
waves, you need to average over the possible initial magnetic quantum
numbers. It may also be noted that the total coefficient
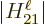 for the decay
for the decay 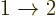 will not be the same as the one
for
will not be the same as the one
for 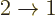 : you average over the initial magnetic quantum
number, but sum over the final one.) If there are different excitation
levels of the final nucleus that can be decayed to, you also need to
sum over these. And if there is more than one type of decay process
going on at the same time, they too need to be added together.
: you average over the initial magnetic quantum
number, but sum over the final one.) If there are different excitation
levels of the final nucleus that can be decayed to, you also need to
sum over these. And if there is more than one type of decay process
going on at the same time, they too need to be added together.
However, all these details are of little importance in finding a
ballpark for the dominant decay process. The real remaining problem
is summing over the electron and antineutrino momentum states. The
total ballparked decay rate must be found from
Based on energy conservation, you would expect that decays should only
occur when the total energy  of the nucleus, electron and
antineutrino after the decay is exactly equal to the energy
of the nucleus, electron and
antineutrino after the decay is exactly equal to the energy 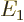 of
the nucleus before the decay. However, the summation above shows that
that is not quite true. For a final state that has
of
the nucleus before the decay. However, the summation above shows that
that is not quite true. For a final state that has  exactly
equal to
exactly
equal to 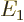 , the last fraction in the summation is seen to be
unity, using l’Hospital. For a final state with an energy
, the last fraction in the summation is seen to be
unity, using l’Hospital. For a final state with an energy  of, for example,
of, for example, 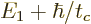 , the ratio is quite comparable.
Therefore decay to such a state proceeds at a comparable rate as to a
state that conserves energy exactly. There is
, the ratio is quite comparable.
Therefore decay to such a state proceeds at a comparable rate as to a
state that conserves energy exactly. There is slop
in
energy conservation.
How can energy not be conserved? The reason is that neither the
initial state nor the final state is an energy eigenstate, strictly
speaking. Energy eigenstates are stationary states. The very fact
that decay occurs assures that these states are not really energy
eigenstates. They have a small amount of uncertainty in energy. The
nonzero value of the Hamiltonian coefficient  assures that,
chapter 5.3, and there may be more decay processes
adding to the uncertainty in energy. If there is some uncertainty in
energy, then
assures that,
chapter 5.3, and there may be more decay processes
adding to the uncertainty in energy. If there is some uncertainty in
energy, then 

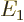 is not an exact relationship.
is not an exact relationship.
To narrow this effect down more precisely, the fraction is plotted in
figure 7.7. The spikes in the figure indicate the energies
 of the possible final states. Now the energy states are almost
infinitely densely spaced, if the periodic box in which the decay is
assumed to occur is big enough. And the box must be assumed very big
anyway, to simulate decay in infinite space. Therefore, the summation
can be replaced by integration, as follows:
of the possible final states. Now the energy states are almost
infinitely densely spaced, if the periodic box in which the decay is
assumed to occur is big enough. And the box must be assumed very big
anyway, to simulate decay in infinite space. Therefore, the summation
can be replaced by integration, as follows:
where 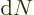

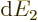 is the number of final states per unit
energy range, often called the density of states
is the number of final states per unit
energy range, often called the density of states  .
.
Now assume that the complete problem is cut into bite-size pieces for
each of which 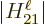 is about constant. It can then be taken out
of the integral. Also, the range of energy in figure 7.7
over which the fraction is appreciable, the energy slop, is very small
on a normal nuclear energy scale: beta decay is a slow process, so the
initial and final states do remain energy eigenstates to a very good
approximation. Energy conservation is almost exactly satisfied.
Because of that, the density of states
is about constant. It can then be taken out
of the integral. Also, the range of energy in figure 7.7
over which the fraction is appreciable, the energy slop, is very small
on a normal nuclear energy scale: beta decay is a slow process, so the
initial and final states do remain energy eigenstates to a very good
approximation. Energy conservation is almost exactly satisfied.
Because of that, the density of states 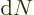

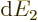 will be
almost constant over the range where the integrand is nonzero. It can
therefore be taken out of the integral too. What is left can be
integrated analytically, [41, 18.36]. That gives:
will be
almost constant over the range where the integrand is nonzero. It can
therefore be taken out of the integral too. What is left can be
integrated analytically, [41, 18.36]. That gives:
That is Fermi’s (second) golden rule.
It describes
how energy slop increases the total decay rate. It is not
specific to beta decay but also applies to other forms of decay to a
continuum of states. Note that it no longer depends on the artificial
length 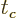 of the time interval over which the system was supposed
to evolve without
of the time interval over which the system was supposed
to evolve without measurement.
That is good news,
since that time interval was obviously poorly defined.
Because of the assumptions involved, like dividing the problem into
bite-size pieces, the above expression is not very intuitive to apply.
It can be rephrased into a more intuitive form that does not depend on
such an assumption. The obtained decay rate is exactly the same as if
in an energy slop range
all states contribute just as much to the decay as one that satisfies
energy conservation exactly, while no states contribute outside of
that range.
(Note that if you ballpark 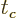 as the half-life, then even a
half-life as short as 10
as the half-life, then even a
half-life as short as 10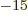 s gives an energy slop of a few eV,
almost impossible to measure. And any nuclear decay with a half life
of 10
s gives an energy slop of a few eV,
almost impossible to measure. And any nuclear decay with a half life
of 10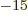 s should surely produce an amount of energy equal to
very many MeV. Outside the mathematics of the Fermi theory, the
energy slop is imperceptible under normal conditions.)
s should surely produce an amount of energy equal to
very many MeV. Outside the mathematics of the Fermi theory, the
energy slop is imperceptible under normal conditions.)
The good news is that phrased this way, it indicates the relevant
physics much more clearly than the earlier purely mathematical
expression for Fermi’s golden rule. The bad news is that it
suffers esthetically from still involving the poorly defined time
 , instead of already having shoved
, instead of already having shoved  under the mat.
Therefore, it is more appealing to write things in terms of the energy
slop altogether:
under the mat.
Therefore, it is more appealing to write things in terms of the energy
slop altogether:
 |
(A.279) |
Here  is the amount that energy conservation seems to be
violated, and is related to a typical time
is the amount that energy conservation seems to be
violated, and is related to a typical time 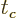 between collisions by
the energy-time uncertainty relationship shown.
between collisions by
the energy-time uncertainty relationship shown.
It may be noted that the golden rule does not apply if the evolution
is not to a continuum of states. It also does not apply if the slop
range  is so large that
is so large that 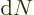

 is not constant
over it. And it does not apply for systems that evolve without being
perturbed over times long enough that the decay probability
becomes significant before the system is
is not constant
over it. And it does not apply for systems that evolve without being
perturbed over times long enough that the decay probability
becomes significant before the system is measured.
(If
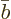 becomes appreciable,
becomes appreciable, 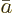 can no longer be close to one
since the probabilities
can no longer be close to one
since the probabilities 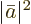 and
and 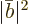 must add to
one.)
must add to
one.) Measurements,
or rather interactions with the larger
environment, are called collisions.
Fermi’s golden
rule applies to so-called collision-dominated
conditions. Typically examples where the conditions are not collision
dominated are in NMR and atomic decays under intense laser light.
Mathematically, the conditions for Fermi’s golden rule can be
written as
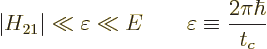 |
(A.280) |
The first inequality means that the perturbation causing the decay
must be weak enough that there is only a small chance of decay before
a collision occurs. The second inequality means that there must be
enough time between collisions that an apparent energy conservation
from initial to final state applies. Roughly speaking, collisions
must be sufficiently frequent on the time scale of the decay process,
but rare on the quantum time scale 

 .
.
It should also be noted that the rule was derived by Dirac, not Fermi.
The way Fermi got his name on it was that he was the one who named it
a golden rule.
Fermi had a flair for finding memorable
names. God knows how he ended up being a physicist.
A.45.6 Mopping up
The previous subsections derived the basics for the rate of beta
decay. The purpose of this section is to pull it all together and get
some actual ballpark estimates for beta decay.
First consider the possible values for the momenta 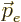 and
and
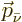 of the electron and antineutrino. Their wave
functions were approximately of the form
of the electron and antineutrino. Their wave
functions were approximately of the form
where 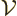

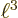 is the volume of the periodic box in which the
decay is assumed to occur.
is the volume of the periodic box in which the
decay is assumed to occur.
In a periodic box the wave function must be the same at opposite sides
of the box. For example, the exponential factor 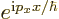 is 1 at
is 1 at  =0, and it must be 1 again at
=0, and it must be 1 again at 

 . That
requires
. That
requires 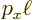

 to be a whole multiple of
to be a whole multiple of  .
Therefore
.
Therefore 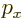 must be a whole multiple of
must be a whole multiple of 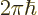

 .
Successive possible
.
Successive possible 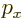 values are therefore spaced the finite
amount
values are therefore spaced the finite
amount 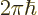

 apart. And so are successive
apart. And so are successive  and
and
 values.
values.
Figure A.27:
Possible momentum states for a particle confined to a
periodic box. The states are shown as points in momentum space.
States that have momentum less than some example maximum value
are in red.
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(380,27...
...l]{$p_y$}}
\put(-45,104.5){\makebox(0,0)[b]{$p_z$}}
\end{picture}
\end{figure}](img5745.gif) |
Graphically this can by visualized by plotting the possible momentum
values as points in a three-dimensional 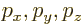 axis system. That is
done in figure A.27. Each point correspond to one
possible momentum state. Each point is the center of its own little
cube with sides
axis system. That is
done in figure A.27. Each point correspond to one
possible momentum state. Each point is the center of its own little
cube with sides 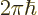

 . The
. The volume
(in this three-dimensional momentum plot, not physical volume) of that
little cube is 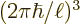 . Since
. Since 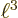 is the
physical volume
is the
physical volume 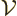 of the periodic box, the
of the periodic box, the volume
in momentum space taken up by each momentum state is
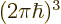

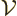
That allows the number of different momentum states to be computed.
In particular, consider how many states have magnitude of momentum
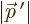 less than some maximum value
less than some maximum value 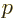 . For some example
value of
. For some example
value of 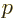 , these are the red states in figure
A.27. Note that they form a sphere of radius
, these are the red states in figure
A.27. Note that they form a sphere of radius 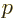 .
That sphere has a
.
That sphere has a volume
equal to
 . Since each state takes up a
. Since each state takes up a
volume
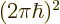

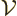 , the number of
states
, the number of
states 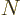 is given by the number of such
is given by the number of such volumes
in
the sphere:
The number of electron states that have momentum in a range from 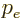 to
to 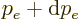 can be found by taking a differential of the
expression above:
can be found by taking a differential of the
expression above:
(Here the range  is assumed small, but not so small that the
fact that the number of states is discrete would show up.) Each
momentum state still needs to be multiplied by the number of
corresponding antineutrino states to find the number of states of the
complete system.
is assumed small, but not so small that the
fact that the number of states is discrete would show up.) Each
momentum state still needs to be multiplied by the number of
corresponding antineutrino states to find the number of states of the
complete system.
Now the kinetic energy of the antineutrino  is fixed in
terms of that of the electron and the energy release of the decay
is fixed in
terms of that of the electron and the energy release of the decay  by:
by:
Here the kinetic energy of the final nucleus is ignored. The heavy
final nucleus is unselfish enough to assure that momentum conservation
is satisfied for whatever the momenta of the electron and antineutrino
are, without demanding a noticeable share of the energy for itself.
That is much like Mother Earth does not take any of the kinetic energy
away if you shoot rockets out to space from different locations. You
might write equations down for it, but the only thing they are going
to tell you is that it is true as long as the speed of the nucleus
does not get close to the speed of light. Beta decays do not release
that much energy by far.
The electron and antineutrino kinetic energies are related to their
momenta by Einstein’s relativistic expression,
chapter 1.1.2:
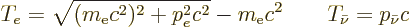 |
(A.281) |
where  is the speed of light and the extremely small rest mass of
the neutrino was ignored. With the neutrino energy fixed, so is the
magnitude of the neutrino momentum:
is the speed of light and the extremely small rest mass of
the neutrino was ignored. With the neutrino energy fixed, so is the
magnitude of the neutrino momentum:
These result shows that the neutrino momentum is fixed for given
electron momentum 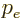 . Therefore there should not be a
neutrino momentum range
. Therefore there should not be a
neutrino momentum range 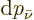 and so no neutrino states.
However, Fermi’s golden rule says that the theoretical energy
after the decay does not need to be exactly the same as the one before
it, because both energies have a bit of uncertainty. This slop in the
energy conservation equation allows a range of energies
and so no neutrino states.
However, Fermi’s golden rule says that the theoretical energy
after the decay does not need to be exactly the same as the one before
it, because both energies have a bit of uncertainty. This slop in the
energy conservation equation allows a range of energies
Therefore the total amount of neutrino states for a given electron
momentum is not zero, but
The number of complete system states in an electron momentum range
 is the product of the number of electron states times the
number of antineutrino states:
is the product of the number of electron states times the
number of antineutrino states:
Each of these states adds a contribution to the specific decay rate
given by
Therefore the total specific decay rate is
where the maximum electron momentum  can be computed from
the
can be computed from
the  -value of the decay using (A.281). (For simplicity
it will be assumed that
-value of the decay using (A.281). (For simplicity
it will be assumed that 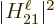 has already been averaged over
all directions of the electron and antineutrino momentum.)
has already been averaged over
all directions of the electron and antineutrino momentum.)
The derived expression (A.277) for the Hamiltonian coefficient
 can be written in the form
can be written in the form
where the overline indicates some suitable average over the directions
of the electron and antineutrino momenta.
It is not easy to say much about 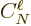 in general, beyond the fact
that its magnitude should not be much more than one. This book will
essentially ignore
in general, beyond the fact
that its magnitude should not be much more than one. This book will
essentially ignore 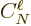 to ballpark the decay rate, assuming that
its variation will surely be much less than that of the beta decay
lifetimes, which vary from milliseconds to 10
to ballpark the decay rate, assuming that
its variation will surely be much less than that of the beta decay
lifetimes, which vary from milliseconds to 10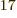 year.
year.
The decay rate becomes after clean up
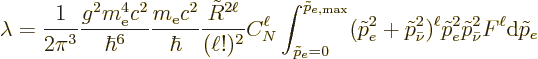 |
(A.282) |
where the 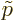 indicate the electron and antineutrino momenta
nondimensionalized with
indicate the electron and antineutrino momenta
nondimensionalized with 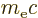 . Also,
. Also,
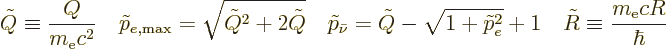 |
(A.283) |
Here 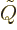 is the
is the  -value or kinetic energy release of the
decay in units of the electron rest mass, and the next two relations
follow from the expression for the relativistic kinetic energy. The
variable
-value or kinetic energy release of the
decay in units of the electron rest mass, and the next two relations
follow from the expression for the relativistic kinetic energy. The
variable  a suitably nondimensionalized nuclear radius, and
is small.
a suitably nondimensionalized nuclear radius, and
is small.
The factor  that popped up out of nothing in the decay rate is
thrown in to correct for the fact that the wave function of the
electron is not really just an exponential. The nucleus pulls on the
electron with its charge, and so changes its wave function locally
significantly. The correction factor
that popped up out of nothing in the decay rate is
thrown in to correct for the fact that the wave function of the
electron is not really just an exponential. The nucleus pulls on the
electron with its charge, and so changes its wave function locally
significantly. The correction factor 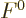 for allowed decays is
called the “Fermi function” and is given by
for allowed decays is
called the “Fermi function” and is given by
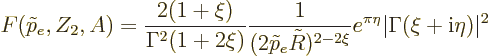 |
(A.284) |
where  is the fine structure constant and
is the fine structure constant and 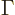 the gamma
function. The nonrelativistic version follows for letting the speed
of light go to infinity, while keeping
the gamma
function. The nonrelativistic version follows for letting the speed
of light go to infinity, while keeping 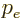

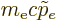 finite.
That gives
finite.
That gives 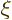
 1 and
1 and
For beta-plus decay, just replace 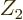 by
by 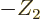 , because an
electron is just as much repelled by a negatively charged nucleus as a
positron is by a positively charged one.
, because an
electron is just as much repelled by a negatively charged nucleus as a
positron is by a positively charged one.
To ballpark the effect of the nuclear charge on the electron wave
function, this book will use the relativistic Fermi function above
whether it is an allowed decay or not.
For allowed decays, the factor in the decay rate that is governed by
the  -value and nuclear charge is
-value and nuclear charge is
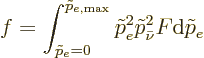 |
(A.285) |
This quantity is known as the “Fermi integral.” Typical values are shown in figure
14.52.
Note that  also depends a bit on the mass number through the
nuclear radius in
also depends a bit on the mass number through the
nuclear radius in  . The figure used
. The figure used
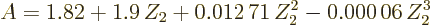 |
(A.286) |
for beta-minus decay and
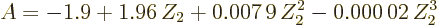 |
(A.287) |
for beta-plus decay, [23].
A.45.7 Electron capture
Electron capture is much more simply to analyze than beta decay,
because the captured electron is in a known initial state.
It will be assumed that a 1s, or K-shell, electron is captured, though
L-shell capture may also contribute to the decay rate for heavy
nuclei. The Hamiltonian coefficient that drives the decay is
In this case, it is an electron annihilation term in the Hamiltonian
that will produce a nonzero term. However, the result will be the
pretty much same; the Hamiltonian coefficient simplifies to
Here 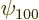 is the hydrogen ground state wave function, but
rescaled for a nucleus of charge
is the hydrogen ground state wave function, but
rescaled for a nucleus of charge 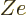 instead of
instead of 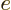 . It does
not contribute to making forbidden decays possible, because
. It does
not contribute to making forbidden decays possible, because
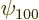 is spherically symmetric. In other words, the 1s
electron has no orbital angular momentum and so cannot contribute to
conservation of angular momentum and parity. Therefore,
is spherically symmetric. In other words, the 1s
electron has no orbital angular momentum and so cannot contribute to
conservation of angular momentum and parity. Therefore, 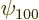 can safely be approximated by its value at the origin, from chapter
4.3,
can safely be approximated by its value at the origin, from chapter
4.3,
where  is the fine-structure constant.
is the fine-structure constant.
The square Hamiltonian coefficient for  th-forbidden decays then
becomes
th-forbidden decays then
becomes
The decay rate for electron capture is
where the first ratio is the decay rate of a single state, with
 the energy slop implied by Fermi’s golden rule.
the energy slop implied by Fermi’s golden rule.
Put it all together, including the fact that there are two K
electrons, and the electron-capture decay rate becomes
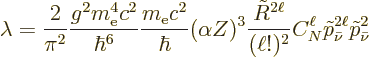 |
(A.288) |
where the  indicate the neutrino momentum
nondimensionalized with
indicate the neutrino momentum
nondimensionalized with 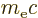 . Also,
. Also,
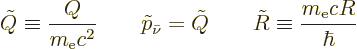 |
(A.289) |
for the coefficients.
![]()
![]()
![]()
![]()
![]() ,
,![]() ,
,![]()
![]()
![]() .
.![]() ,
,![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]() ,
,![]()
![]()
![]() :
:![]()
![]()
![]() ;
;![]()
![]() .
.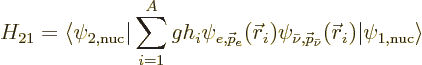
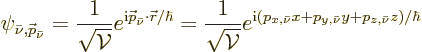

![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]() .
.![]() ,
,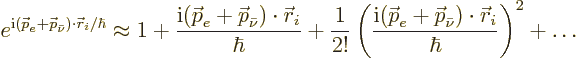
![]() ,
,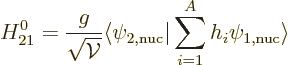
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]() ,
,![]()
![]() .
.![]()
![]() .
.![]()
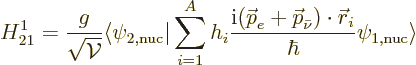

![]()
![]()
![]()
![]() ,
,![]()
![]() t
t![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]() ,
,![]()
![]()
![]() .
.![]()
![]()
![]()
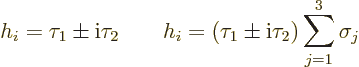
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]() .
.![]()
![]()
![]() .
.![]() .
.![]()
![]() ,
,![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
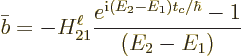
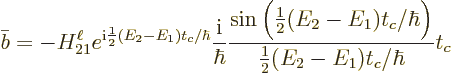
![]() ,
,![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() :
: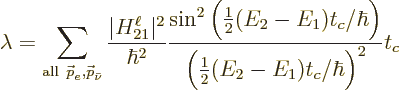
![]()
![]()
![]()
![]() ,
,![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
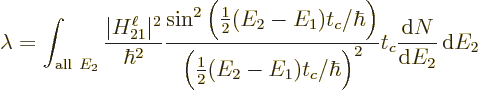
![]()
![]()
![]()
![]()
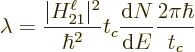
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
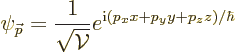
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(380,27...
...l]{$p_y$}}
\put(-45,104.5){\makebox(0,0)[b]{$p_z$}}
\end{picture}
\end{figure}](img5745.gif)
![]()
![]()
![]()
![]() .
.![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]() ,
,![]() .
.![]() .
.![]()
![]()
![]() ,
,![]()
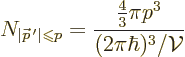
![]()
![]()
![]()
![]()
![]() .
.![]()
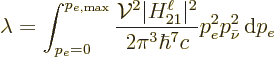
![]()
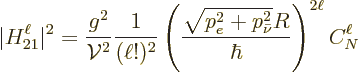
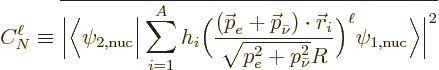
![]()
![]()
![]()
![]()
![]()
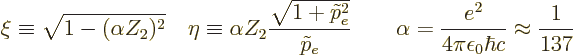
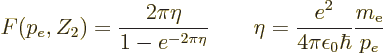
![]() -
-![]()
![]() .
.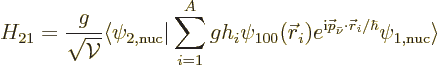
![]()
![]()
![]() .
.![]()
![]()
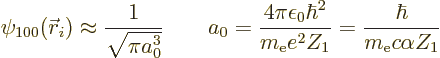
![]() t
t
