|
|
|
|
|
Next: 14.19 Draft: Beta decay |
|
Isospin is another way of thinking about the two types of nucleons. It has proved quite useful in understanding nuclei, as well as elementary particles.
Normally, you think of nuclei as consisting of protons and neutrons. But protons and neutrons are very similar in properties, if you ignore the Coulomb force. They have almost the same mass. Also, according to charge independence, the nuclear force is almost the same whether it is protons or neutrons.
So suppose you define only one particle, called nucleon. Then you can
give that particle an additional property called “nucleon
type.” If the nucleon type is ![]() ,
,![]()
![]()
![]() -
-nucleon-type axis.
Therefore nucleon type
is conventionally indicated by the symbol ![]() ,
,![]() ,
,
| (14.40) |
So far, all this it may seem like a stupid mathematical trick. And normally it would be. The purpose of mathematical analysis is to understand systems, not to make them even more incomprehensible.
But to the approximation that the nuclear force is charge-independent,
nucleon type is not so stupid after all. If the nuclear force is
charge-independent, and the Coulomb force is ignored, you can write
down nuclear wave functions without looking at the nucleon type. Now
suppose that in doing so, you find some energy eigenfunction of the
form
That is fine if nucleon 1 is a proton and nucleon 2 a neutron. Or vice-versa. But it is not OK if both nucleons are protons, or if they are both neutrons. Wave functions must change sign if two identical fermions are exchanged. That is the antisymmetrization requirement. The wave function above stays the same. So it is only acceptable for the deuteron, with one proton and one neutron.
Next suppose you could find a different wave function of the form
diproton” and the “dineutron.(The prefix
dimeans two.)
That would give nontrivial insight in nuclear energy levels. It would
mean physically that the diproton, the dineutron, and the deuteron can
be in an identical energy state. Such identical energy states,
occurring for different nuclei, are called “isobaric analog (or analogue) states.” Or “charge states.” Or “isobaric multiplets.” Or “![]() -
-
Disappointingly, in real life there is no bound state of the form
![]() .
.
Within the approximations of charge independence and negligible Coulomb effects, whether a given state applies to a given set of nucleon types depends only on the antisymmetrization requirements.Now for bigger systems of nucleons, the antisymmetrization requirements get much more complex. A suitable formalism for dealing with that has already been developed in the context of the spin of systems of identical fermions. It is convenient to adopt that formalism also for nucleon type.
As an example, consider the above three hypothetical isobaric analog
states for the diproton, dineutron, and deuteron. They can be written
out separately as, respectively,

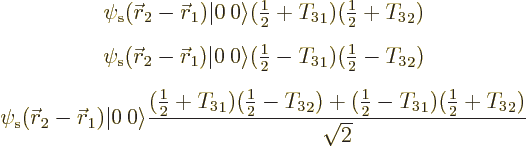
The third wave function represents something of a change in thinking. It requires that one nucleon is a proton and the other a neutron. So it is a wave function for the deuteron. But the actual wave function above is a superposition of two states. In the first state, nucleon 1 is the proton and nucleon 2 the neutron. In the second state, nucleon 1 is the neutron and nucleon 2 the proton. In the combined state the nucleons have lost their identity. It is uncertain whether nucleon 1 is the proton and nucleon 2 the neutron, or vice-versa.
Within the formalism of identical nucleons that have an additional nucleon-type property, this uncertainty in nucleon types is unavoidable. The wave function would not be antisymmetric under nucleon exchange without it. But if you think about it, this may actually be an improvement in the description of the physics. Protons and neutrons do swap identities. That happens if they exchange a charged pion. Proton-neutron scattering experiments show that they can do that. For nucleons that have a probability of swapping type, assigning a fixed type in energy eigenstates is not right. Energy eigenstates must be stationary. And having a better description of the physics can affect what sort of potentials you would want to write down for the nucleons.
(You might think that without charge independence, the additional
antisymmetrization requirement for identical nucleons would change the
physics. But actually, it does not. The antisymmetrization
requirement can be accomodated by uncertainty in which nucleon you
label 1 and which 2. Consider some completely general proton-neutron
wave function
![]() ,
,
entirely useless,as Wigner was the first to point out, [50, p. 4].)
Now compare the trailing nucleon-type factors in the three
hypothetical isobaric analog states above with the possible combined
spin states of two spin ![]()
triplet
spin states, (5.26). So define
similarly
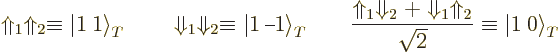 |
(14.42) |
Now reconsider the wave function for two nucleons that was written
down first. The one that was only acceptable for the deuteron. In
the same terminology, it can be written as

Of course, all this raises the question what to make of the leading 0
in the singlet state ![]() ,
,![]() ?
?![]()
![]() ,
,![]() ,
,![]()
components.
![]() ”
”![]()
However, it is possible to define such components in complete analogy
with the ![]()
![]()
![]()
![]()
To do so, first an operator ![]()
![]()
| (14.43) |
Next a “charge creation operator” is defined by
| (14.44) |
| (14.45) |
| (14.46) |
With these operators, square nucleon type can be defined just like square spin. All the mathematics has been forced to be the same.
The quantum number of square nucleon type will be indicated by ![]()
![]()
![]()
In any case there are three scaled operators whose definition and
symbols are fairly standard in most sources. These are defined as
| (14.47) |
Now consider an example of isobaric analog states that actually exist. In this case the nucleons involved are carbon-14, nitrogen-14, and oxygen-14. All three have 14 nucleons, so they are isobars. However, carbon-14 has 6 protons and 8 neutrons, while oxygen-14 has 8 protons and 6 neutrons. Such pairs of nuclei, that have their numbers of protons and neutrons swapped, are called “conjugate” nuclei. Or “mirror” nuclei. Nitrogen-14 has 7 protons and 7 neutrons and is called “self-conjugate.”
Since ![]()
![]()
![]()
![]()
![]()
![]() 1
1![]()
![]()
![]()
![]()
In general, 14 nucleons can have a maximum ![]()
![]()
![]() 7
7
Here is where the analogy with spin angular momentum gets interesting.
Angular momentum is a vector. A given angular momentum vector can
still have different directions. And different directions means
different values of the ![]() -
-![]() .
.![]()
Since nucleon type has been defined to be completely equivalent to
spin, essentially the same holds. A given nucleon energy state can
still have different values of ![]() :
:
| (14.49) |
You could say that isobaric analog states arise because
rotating
an energy state in the abstract 1,2,3-space
defined above does not make a difference. And the reason it does not
make a difference is charge independence.
Based on the values of ![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
It turns out that light nuclei in their ground state generally have
the smallest value of ![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
(Another argument, offered in literature, is essentially the reverse
of the one that gives rise to the so-called Hund rule
for atoms. Simply put, the Hund rule says that a couple of electrons
maximize their spin, given the option between single-particle states
of the same energy. The reason is that this allows electrons to stay
farther apart, reducing their Coulomb repulsion,
{A.34}. This argument reverses for nucleons, since
they normally attract rather than repel each other. However, surely
this is a relatively minor effect? Consider 3 nucleons. For these,
the highest value ![]()
![]()
![]()
![]()
![]()
![]()
For the deuteron ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
But it is true. Figure 14.46 shows the energy levels of carbon-14, nitrogen-14, and oxygen-14. More precisely, it shows their binding energy, relative to the ground state value for nitrogen-14. In addition the von Weizsäcker value for the Coulomb energy has been subtracted to more clearly isolate the nuclear force effects. (The combined effect is simply to shift the normal spectra of carbon-14 and oxygen-14 up by 2.83, respectively 1.89 MeV.) It is seen that nitrogen-14 is indeed more tightly bound in its ground state than carbon-14 and oxygen-14. Qualitatively, since nitrogen-14 does not have 8 nucleons of the same kind, it has an easier job with satisfying the antisymmetrization requirements.
Traces of the lower energy of light nuclei with ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Carbon-14 and oxygen-14 are mirror nuclei, so you would expect them to
have pretty much the same sort of energy levels. Indeed, any
oxygen-14 state, having ![]()
![]()
![]()
![]()
![]()
![]() 1
1![]()
![]()
![]()
Now each of these multiplets should also have a version with ![]()
![]()
![]()
![]()
![]()
Ideally speaking, these three states should have the same height in the figure. But it would be difficult to remove the Coulomb effect completely. And charge independence is not exact either, even though it is quite accurate.
A similar ![]()
![]()
![]()
![]()
![]()
Figure 14.46 also shows that nitrogen-14 has a lot more
low energy states than carbon-14 or oxygen-14. Square nucleon type
can explain that too: all the low-lying states of nitrogen-14 that are
not shared with carbon-14 and oxygen-14 are ![]()
![]()
Nothing is perfect, of course. The first state with nonzero ![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
Despite such imperfections, consideration of nucleon type is quite helpful for understanding the energy levels of light nuclei. And a lot of it carries over to heavier nuclei, [50, p. 12] and [36, p. 57]. While heavier nuclei have significant Coulomb energy, this long-range force is apparently often not that important here.
Now all that is needed is a good name. Nucleon type
or
nucleon class
are not acceptable; they would give
those hated outsiders and pesky students a general idea of what
physicists were talking about. However, physicists noted that there
is a considerable potential for confusion between nucleon type and
spin, since both are described by the same mathematics. To maximize
that potential for confusion, physicists decided that nucleon type
should be called spin.
Of course, physicists themselves still have to know whether they are
talking about nucleon type or spin. Therefore some physicists called
nucleon type isobaric spin,
because what
differentiates isobars is the value of the net ![]() .
.isotopic spin,
because
physicists like to think of isotopes, and hey, isotopes have nucleon
type too. Some physicists took the isowhatever spin to be ![]()
![]() .
.spin
being
talked about was not really spin. If you think about it,
isobaric angular momentum
or “isotopic angular
momentum” does not make much sense. So physicists shortened
the name to isospin.
Isospin means “equal
spin” plain and simple; there is no longer anything to give the
secret away that it is something completely different from spin.
However, the confusion of having two different names for the same
quantity was missed. Therefore, the alternate term
i-spin
was coined besides isospin. It too has
nothing to give the secret away, and it restores that additional touch
of confusion.
Isospin is conserved when only the nuclear force is relevant. As an
example, consider the reaction in which a deuteron kicks an alpha
particle out of an oxygen-16 nucleus:
Selection rules for which nuclear decays occur can also be formulated
based on isospin. If the electromagnetic force plays a significant
part, ![]()
![]()
![]()
![]()
![]() .
.superallowed,
because it is unusually fast. It is
much faster than to the ground state, even though decay to the ground
state releases more energy. Carbon-14 has too little energy to decay
to the analog state.)
Despite the lack of isospin conservation, isospin turns out to be very useful for understanding beta and gamma decay. See for example the discussion of superallowed beta decays in chapter 14.19, and the isospin selection rules for gamma decay in section 14.20.2.
There are other particles besides nucleons that are also pretty much
the same except for electric charge, and that can also be described
using isospin. For example, the positive, neutral, and negatively
charged pions form an isospin triplet of states with ![]()
![]()
Some sources incorrectly credit the concept of isospin to Heisenberg. But he did not understand what he was doing. Heisenberg did correctly guess that protons and neutrons might be described as two variants of the same particle. He then applied the only quantum approach for a two-state particle to it that he knew, that of spin. However, the mathematical machinery of spin is designed to deal with two-state properties that are preserved under rotations of an axis system, compare {A.19}. That is an inappropriate mathematical approach to describe nucleon type in the absence of charge independence. And at the time Heisenberg himself believed that the nuclear force was far from charge-independent.
(Because the nuclear force is in fact approximately
charge-independent, unlike Heisenberg assumed, isospin is preserved
under rotations of the abstract 1,2,3 coordinate system as defined in
the first subsection. Phrased more simply, without charge
independence, energy eigenfunctions would not have definite values of
square isospin ![]() .
.entirely useless,
as Wigner pointed out. This point
is not very clear from the example of two nucleons in empty space, as
discussed above. That is because there the spatial wave function
happens to be symmetric under particle exchange even without charge
independence. But if you express the isospin states in the general
wave function (14.41) in terms of the singlet and triplet
states, you quickly see the problem.)
The recognition that isospin was meaningful only in the presence of
charge independence, and the proposal that the nuclear force is indeed
quite accurately charge-independent, was mostly due to Wigner,
in part with Feenberg. Some initial steps had already been taken by
other authors. In particular, Cassen & Condon had already proposed
to write wave functions in a form to include isospin,
nucleon typeshould be called
spin.
See Wilkinson, [50, p. vi, 1-13], for a more extensive discussion of these historical issues. A very different history is painted by Henley in the next chapter in the same book. In this history, Heisenberg receives all the credit. Wigner does not exist. However, the author of this history implicitly admits that Heisenberg did think that the nuclear force was far from charge-independent. Maybe the author understood isospin too poorly to recognize that that is a rather big problem. Certainly there is no discussion. Or the author had a personal issue with Wigner and was willing to sacrifice his scientific integrity for it. Either way, the credibility of the author of this particular history is zero.
It may seem astonishing that all this works. Why would nucleon type resemble spin? Spin is a vector in three-dimensional space, not a simple number. Why would energy eigenstates be unchanged under rotations in some weird abstract space?
The simplest and maybe best answer is that nature likes this sort of mathematics. Nature just loves creation and annihilation operators. But still, why would that lead to preserved lengths of vectors in an abstract spaces?
An answer can be obtained by looking a bit closer at square spin.
Consider first two spin ![]()
![]()
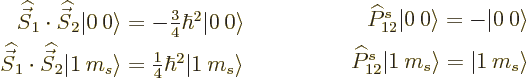
Comparing the two sets of relations, it is seen that the dot product
of two spins is closely related to the operator that exchanges the two
spins:
Now consider the square spin of a system of ![]()
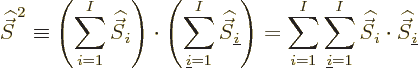
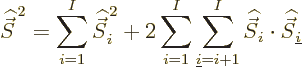
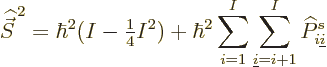
Similarly then for isospin as defined in the first subsection,

It may be noted that the exchange operators do not commute among
themselves. That makes the symmetry requirements so messy. However,
it is possible to restrict consideration to exchange operators of the
form ![]() .
.
Infinitesimal rotations
of a state in 1,2,3 isospin
state correspond to applying small multiples of the operators
![]() ,
,![]()
![]() ,
,![]()
![]() ,
,![]()