| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
Subsections
14.17 Draft: Electromagnetic Moments
The most important electromagnetic property of nuclei is their net
charge. It is what keeps the electrons in atoms and molecules
together. However, nuclei are not really electric point charges.
They have a small size. In a spatially varying electric field most
respond somewhat different than a point charge. It is said that they
have an electric quadrupole moment. Also, most nuclei act like little
electromagnets. It is said that they have a “magnetic dipole
moment.” These properties are important for applications like
NMR and MRI, and for experimentally examining nuclei.
14.17.1 Draft: Classical description
This subsection explains the magnetic dipole and electric quadrupole
moments from a classical point of view.
14.17.1.1 Draft: Magnetic dipole moment
The most basic description of an electromagnet is charges going around
in circles. It can be seen from either classical or quantum
electromagnetics that the strength of an electromagnet is proportional
to the angular momentum  of the charges times the ratio of
their charge
of the charges times the ratio of
their charge  to their mass
to their mass  , chapter 13.2 or
13.4.
, chapter 13.2 or
13.4.
This leads to the definition of the magnetic dipole moment as
In particular, a magnet wants to align itself with an external
magnetic field 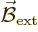 . The energy involved in this
alignment is
. The energy involved in this
alignment is
14.17.1.2 Draft: Electric quadrupole moment
Consider a nuclear charge distribution with charge density 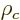 placed in an external electrical potential, or
placed in an external electrical potential, or voltage
 . The potential energy due to the external field is
. The potential energy due to the external field is
It may be noted that since nuclear energies are of the order of MeV,
an external field is not going to change the nuclear charge
distribution  . It would need to have a million volt drop
over a couple of femtometers to make a dent in it. Unless you shoot
very high energy charged particles at the nucleus, that is not going
to happen. Also, the current discussion assumes that the external
field is steady or at least quasi-steady. That should be reasonable
in many cases, as nuclear internal time scales are very fast.
. It would need to have a million volt drop
over a couple of femtometers to make a dent in it. Unless you shoot
very high energy charged particles at the nucleus, that is not going
to happen. Also, the current discussion assumes that the external
field is steady or at least quasi-steady. That should be reasonable
in many cases, as nuclear internal time scales are very fast.
Since nuclei are so small compared to normal external fields, the
electric potential  can be well represented by a Taylor
series. That gives the potential energy as
can be well represented by a Taylor
series. That gives the potential energy as
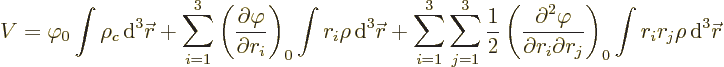
where 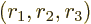

 are the three components of position and
0 indicates that the derivative is evaluated at the origin, the center
of the nucleus.
are the three components of position and
0 indicates that the derivative is evaluated at the origin, the center
of the nucleus.
The first integral in the expression above is just the net nuclear
charge  . This makes the first term exactly the same as the
potential energy of a point charge. The second integral defines the
. This makes the first term exactly the same as the
potential energy of a point charge. The second integral defines the
electric dipole moment
in the  -direction. It
is nonzero if on average the charge is shifted somewhat towards one
side of the nucleus. But nuclei do not have nonzero electric dipole
moments. The reason is that nuclei have definite parity; the wave
function is either the same or the same save for a minus sign when you
look at the opposite side of the nucleus. Since the probability of a
proton to be found at a given position is proportional to the square
magnitude of the wave function, it is just as likely to be found at
one side as the other one. (That should really be put more precisely
for the picky. The dipole contribution of any set of positions of the
protons is canceled by an opposite contribution from the set of
opposite nucleon positions.)
-direction. It
is nonzero if on average the charge is shifted somewhat towards one
side of the nucleus. But nuclei do not have nonzero electric dipole
moments. The reason is that nuclei have definite parity; the wave
function is either the same or the same save for a minus sign when you
look at the opposite side of the nucleus. Since the probability of a
proton to be found at a given position is proportional to the square
magnitude of the wave function, it is just as likely to be found at
one side as the other one. (That should really be put more precisely
for the picky. The dipole contribution of any set of positions of the
protons is canceled by an opposite contribution from the set of
opposite nucleon positions.)
The last integral in the expression for the potential energy defines
the quadrupole matrix or tensor. You may note a mathematical
similarity with the moment of inertia matrix of a solid body in
classical mechanics. Just like there, the quadrupole matrix can be
simplified by rotating the coordinate system to principal axes. That
rotation gets rid of the integrals  for
for 
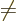
 , so what is left is
, so what is left is
where the first term is the potential of the point charge.
Note that the average of 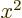 ,
, 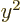 , and
, and 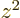 is
is
 . It is convenient to subtract that average in each
integral. The subtraction does not change the value of the potential
energy. The reason is that the sum of the three second order
derivatives of the external field
. It is convenient to subtract that average in each
integral. The subtraction does not change the value of the potential
energy. The reason is that the sum of the three second order
derivatives of the external field  is zero due to
Maxwell”s first equation, chapter 13.2. All that
then leads to a definition of an electric quadrupole moment for a
single axis, taken to be the
is zero due to
Maxwell”s first equation, chapter 13.2. All that
then leads to a definition of an electric quadrupole moment for a
single axis, taken to be the  -axis, as
-axis, as
For simplicity, the nasty fractions have been excluded from the
definition of  . Also, it has been scaled with the charge
. Also, it has been scaled with the charge 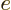 of a single proton.
of a single proton.
That gives  units of square length, which is easy to put in
context. Recall that nuclear sizes are of the order of a few
femtometer. So the SI unit square femtometer, fm
units of square length, which is easy to put in
context. Recall that nuclear sizes are of the order of a few
femtometer. So the SI unit square femtometer, fm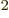 or
10
or
10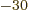 m
m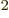 , works quite nicely for the quadrupole moment
, works quite nicely for the quadrupole moment
 as defined. It is therefore needless to say that most sources do
not use it. They use the “barn,” a non-SI unit equal to 10
as defined. It is therefore needless to say that most sources do
not use it. They use the “barn,” a non-SI unit equal to 10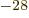 m
m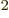 . The
reason is historical; during the second world war some physicists
figured that the word
. The
reason is historical; during the second world war some physicists
figured that the word barn
would hide the fact that
work was being done on nuclear bombs from the Germans. Of course,
that did not work since so few memos and reports are one-word ones.
However, physicists discovered that it did help confuse students, so
the term has become very widely used in the half century since then.
Also, unlike a square femtometer, the barn is much too large compared
to a typical nuclear cross section, producing all these sophisticated
looking tiny decimal fractions.
To better understand the likely values of the quadrupole moment,
consider the effect of the charge distribution of a single proton. If
the charge distribution is spherically symmetric, the averages of
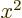 ,
, 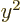 and
and 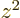 are equal, making
are equal, making  zero. However,
consider the possibility that the charge distribution is not
spherical, but an ellipsoid of revolution, a “spheroid.”. If the axis of symmetry is the
zero. However,
consider the possibility that the charge distribution is not
spherical, but an ellipsoid of revolution, a “spheroid.”. If the axis of symmetry is the  -axis, and
the charge distribution hugs closely to that axis, the spheroid will
look like a cigar or zeppelin. Such a spheroid is called“prolate.” The value of
-axis, and
the charge distribution hugs closely to that axis, the spheroid will
look like a cigar or zeppelin. Such a spheroid is called“prolate.” The value of  is then about
is then about 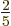 of the
square nuclear radius
of the
square nuclear radius  . If the charge distribution stays
close to the
. If the charge distribution stays
close to the 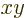 -plane, the spheroid will look like a flattened
sphere. Such a spheroid is called “oblate.” In that case the value of
-plane, the spheroid will look like a flattened
sphere. Such a spheroid is called “oblate.” In that case the value of  is about
is about 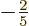 of
the square nuclear radius. Either way, the values of
of
the square nuclear radius. Either way, the values of  are
noticeably less than the square nuclear radius.
are
noticeably less than the square nuclear radius.
It may be noted that the quadrupole integrals also pop up in the
description of the electric field of the nucleus itself. Far from the
nucleus, the deviations in its electric field from that of a point
charge are proportional to the same integrals, compare chapter
13.3.3.
14.17.2 Draft: Quantum description
Quantum mechanics makes for some changes to the classical description
of the electromagnetic moments. Angular momentum is quantized, and
spin must be included.
14.17.2.1 Draft: Magnetic dipole moment
As the classical description showed, the strength of an electromagnet
is essentially the angular momentum of the charges going around, times
the ratio of their charge to their mass. In quantum mechanics angular
momentum comes in units of  . Also, for nuclei the
charged particles are protons with charge
. Also, for nuclei the
charged particles are protons with charge 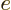 and mass
and mass 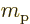 .
Therefore, a good unit to describe magnetic strengths in terms of is
the so-called “nuclear magneton”
.
Therefore, a good unit to describe magnetic strengths in terms of is
the so-called “nuclear magneton”
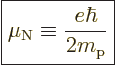 |
(14.26) |
In those terms, the magnetic magnetic dipole moment operator of a
single proton is
But quantum mechanics brings in a complication, chapter
13.4. Protons have intrinsic angular momentum, called
spin. That also acts as an electromagnet. In addition the magnetic
strength per unit of angular momentum is different for spin than for
orbital angular momentum. The factor that it is different is called
the proton  -factor
-factor 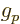 . That then makes the total magnetic
dipole moment operator of a single proton equal to
. That then makes the total magnetic
dipole moment operator of a single proton equal to
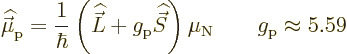 |
(14.27) |
The above value of the proton  -factor is experimental.
-factor is experimental.
Neutrons do not have charge and therefore their orbital motion creates
no magnetic moment. However, neutrons do create a magnetic moment
through their spin:
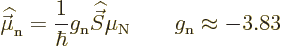 |
(14.28) |
The reason is that the neutron consists of three charged quarks; they
produce a net magnetic moment even if they do not produce a net
charge.
The net magnetic dipole moment operator of the complete nucleus is
![\begin{displaymath}
{\skew 4\widehat{\skew{-.5}\vec\mu}}= \frac{1}{\hbar}
\lef...
...}^A g_{\rm n} {\skew 6\widehat{\vec S}}_i
\right] \mu_{\rm N}
\end{displaymath}](img3332.gif) |
(14.29) |
where  is the nucleon number, the first
is the nucleon number, the first 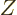 being protons and
the rest neutrons.
being protons and
the rest neutrons.
Now assume that the nucleus is placed in an external magnetic field
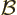 and take the
and take the  -axis in the direction of the field. Because
nuclear energies are so large, external electromagnetic fields are far
too weak to change the quantum structure of the nucleus; its wave
function remains unchanged to a very good approximation. However, the
field does produce a tiny change in the energy levels of the quantum
states. These may be found using expectation values:
-axis in the direction of the field. Because
nuclear energies are so large, external electromagnetic fields are far
too weak to change the quantum structure of the nucleus; its wave
function remains unchanged to a very good approximation. However, the
field does produce a tiny change in the energy levels of the quantum
states. These may be found using expectation values:
The fact that that is possible is a consequence of small perturbation
theory, as covered in addendum {A.38}.
However, it is not immediately clear what nuclear wave function  to use in the expectation value above. Because of the large values of
nuclear energies, a nucleus is affected very little by its
surroundings. It behaves essentially as if it is isolated in empty
space. That means that while the nuclear energy may depend on the
magnitude of the nuclear spin
to use in the expectation value above. Because of the large values of
nuclear energies, a nucleus is affected very little by its
surroundings. It behaves essentially as if it is isolated in empty
space. That means that while the nuclear energy may depend on the
magnitude of the nuclear spin 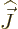 , (i.e. the net nuclear
angular momentum), it does not depend on its direction. In quantum
terms, the energy does not depend on the component
, (i.e. the net nuclear
angular momentum), it does not depend on its direction. In quantum
terms, the energy does not depend on the component 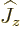 in the
chosen
in the
chosen  -direction. So, what should be used in the above
expectation value to find the change in the energy of a nucleus in a
state of spin
-direction. So, what should be used in the above
expectation value to find the change in the energy of a nucleus in a
state of spin  ? States with definite values of
? States with definite values of 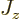 ?
Linear combinations of such states? You get a difference answer
depending on what you choose.
?
Linear combinations of such states? You get a difference answer
depending on what you choose.
Now a nucleus is a composite structure, consisting of protons or
neutrons, each contributing to the net magnetic moment. However, the
protons and neutrons themselves are composite structures too, each
consisting of three quarks. Yet at normal energy levels protons and
neutrons act as elementary particles, whose magnetic dipole moment is
a scalar multiple 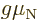 of their spin. Their energies in a magnetic
field split into two values, one for the state with
of their spin. Their energies in a magnetic
field split into two values, one for the state with 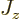

 and the other with
and the other with 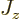

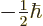 .
One state corresponds to magnetic quantum number
.
One state corresponds to magnetic quantum number 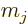

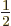 , the other to
, the other to 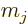

 .
.
The same turns out to be true for nuclei; they too behave as
elementary particles as long as their wave functions stay intact. In a
magnetic field, the original energy level of a nucleus with spin  splits into equally spaced levels corresponding to nuclear magnetic
quantum numbers
splits into equally spaced levels corresponding to nuclear magnetic
quantum numbers 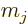

 . The numerical
value of the magnetic dipole moment
. The numerical
value of the magnetic dipole moment  is therefore defined
to be the expectation value of
is therefore defined
to be the expectation value of  in the nuclear state in which
in the nuclear state in which
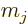 has its largest value
has its largest value  , call it the
, call it the  state:
state:
 |
(14.30) |
The fact that nuclei would behave so simple is related to the fact
that nuclei are essentially in empty space. That implies that the
complete wave function of a nucleus in the ground state, or another
energy eigenstate, will vary in a very simple way with angular
direction. Furthermore, that variation is directly given by the
angular momentum of the nucleus. A brief discussion can be found in
chapter 7.3 and its note. See also the discussion of
the Zeeman effect, and in particular the weak Zeeman effect, in
addendum {A.38}.
The most important consequence of those ideas is that
Nuclei with spin zero do not have magnetic dipole moments.
That is not very easy to see from the general expression for the
magnetic moment, cluttered as it is with  -factors. However, zero
spin means on a very fundamental level that the complete wave function
of a nucleus is independent of direction, chapter 4.2.3. A
magnetic dipole strength requires directionality, there must be a
north pole and a south pole. That cannot occur for nuclei of spin
zero.
-factors. However, zero
spin means on a very fundamental level that the complete wave function
of a nucleus is independent of direction, chapter 4.2.3. A
magnetic dipole strength requires directionality, there must be a
north pole and a south pole. That cannot occur for nuclei of spin
zero.
14.17.2.2 Draft: Electric quadrupole moment
The definition of the electric quadrupole moment follows the same
ideas as that of the magnetic dipole moment. The numerical value of
the quadrupole moment is defined as the expectation value of
 , summed over all protons, in the state in which the
net nuclear magnetic quantum number
, summed over all protons, in the state in which the
net nuclear magnetic quantum number 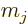 equals the nuclear spin
equals the nuclear spin
 :
:
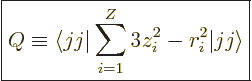 |
(14.31) |
Note that there is a close relation with the spherical harmonics;
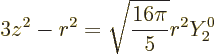 |
(14.32) |
That is important because it implies that
Nuclei with spin zero or with spin one-half do not have electric
quadrupole moments.
To see why, note that the expectation value involves the absolute
square of the wave function. Now if you multiply two wave functions
together that have an angular dependence corresponding to a spin
 , mathematically speaking you get pretty much the angular
dependence of two particles of spin
, mathematically speaking you get pretty much the angular
dependence of two particles of spin  . That cannot become
more than an angular dependence of spin
. That cannot become
more than an angular dependence of spin 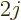 , in other words an
angular dependence with terms proportional to
, in other words an
angular dependence with terms proportional to 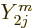 . Since
the spherical harmonics are mutually orthonormal,
. Since
the spherical harmonics are mutually orthonormal, 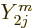 integrates away against
integrates away against 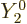 for
for 

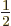 .
.
It makes nuclei with spin  popular for nuclear magnetic
resonance studies. Without the perturbing effects due to quadrupole
interaction with the electric field, they give nice sharp signals.
Also of course, analysis is easier with only two spin states and no
quadrupole moment.
popular for nuclear magnetic
resonance studies. Without the perturbing effects due to quadrupole
interaction with the electric field, they give nice sharp signals.
Also of course, analysis is easier with only two spin states and no
quadrupole moment.
14.17.2.3 Draft: Shell model values
According to the odd-particle shell model, all even-even nuclei have
spin zero and therefore no magnetic or electric moments. That is
perfectly correct.
For nuclei with an odd mass number, the model says that all nucleons
except for the last odd one are paired up in spherically symmetric
states of zero spin that produce no magnetic moment. Therefore, the
magnetic moment comes from the last proton or neutron. To get it,
according to the second last subsubsection, what is needed is the
expectation value of the magnetic moment operator  as given
there. Assume the shell that the odd nucleon is in has
single-particle net momentum
as given
there. Assume the shell that the odd nucleon is in has
single-particle net momentum  . According to the definition
of magnetic moment, the magnetic quantum number must have its maximum
value
. According to the definition
of magnetic moment, the magnetic quantum number must have its maximum
value 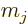

 . Call the corresponding state the
. Call the corresponding state the
 one because the spectroscopic notation is useless as
always. In particular for an odd-even nucleus,
one because the spectroscopic notation is useless as
always. In particular for an odd-even nucleus,
while for an even-odd nucleus
The unit 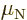 is the nuclear magneton. The expectation values can
be evaluated by writing the state
is the nuclear magneton. The expectation values can
be evaluated by writing the state  in terms of the
component states
in terms of the
component states 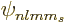 of definite angular momentum
of definite angular momentum
 and spin
and spin  following chapter 12.8,
2.
following chapter 12.8,
2.
It is then found that for an odd proton, the magnetic moment is
 |
(14.33) |
while for an odd neutron
 |
(14.34) |
These are called the “Schmidt values.”
Odd-odd nuclei are too messy to be covered here, even if the Nordheim
rules would be reliable.
For the quadrupole moments of nuclei of odd mass number, filled shells
do not produce a quadrupole moment, because they are spherically
symmetric. Consider now first the case that there is a single proton
in an otherwise empty shell with single-particle momentum  .
Then the magnetic moment of the nucleus can be found as the one of
that proton:
.
Then the magnetic moment of the nucleus can be found as the one of
that proton:
Evaluation, {D.78}, gives
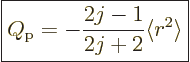 |
(14.35) |
where 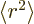 is the expectation value of
is the expectation value of 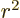 for the
proton. Note that this is zero as it should if the spin
for the
proton. Note that this is zero as it should if the spin 

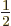 . Since the spin
. Since the spin  must be half-integer, zero spin
is not a consideration. For all other values of
must be half-integer, zero spin
is not a consideration. For all other values of  , the
one-proton quadrupole moment is negative.
, the
one-proton quadrupole moment is negative.
The expectation value 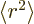 can hardly be much more
than the square nuclear radius, excepting maybe halo nuclei. A
reasonable guess would be to assume that the proton is homogeneously
distributed within the nuclear radius
can hardly be much more
than the square nuclear radius, excepting maybe halo nuclei. A
reasonable guess would be to assume that the proton is homogeneously
distributed within the nuclear radius  . That gives a
ballpark value
. That gives a
ballpark value
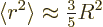
Next consider the case that there are not one but 
 3 protons
in the unfilled shell. The picture of the odd-particle shell model as
usually painted is: the first
3 protons
in the unfilled shell. The picture of the odd-particle shell model as
usually painted is: the first  protons are pairwise combined in
spherically symmetric states and the last odd proton is in a single
particle state, blissfully unaware of the other protons in the shell.
In that case, the quadrupole moment would self evidently be the same
as for one proton in the shell. But as already pointed out in section
14.12.4, the painted picture is not really correct. For one,
it does not satisfy the antisymmetrization requirement for all
combinations on protons. There really are
protons are pairwise combined in
spherically symmetric states and the last odd proton is in a single
particle state, blissfully unaware of the other protons in the shell.
In that case, the quadrupole moment would self evidently be the same
as for one proton in the shell. But as already pointed out in section
14.12.4, the painted picture is not really correct. For one,
it does not satisfy the antisymmetrization requirement for all
combinations on protons. There really are  protons in the shell
sharing one wave function that produces a net spin equal to
protons in the shell
sharing one wave function that produces a net spin equal to  .
.
In particular consider the case that there are 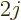 protons in the
shell. Then the wave function takes the form of a filled shell,
having no quadrupole moment, plus a
protons in the
shell. Then the wave function takes the form of a filled shell,
having no quadrupole moment, plus a hole
, a state of
angular momentum  for the missing proton. Since a proton hole has
minus the charge of a proton, the quadrupole moment for a single hole
is opposite to that of one proton:
for the missing proton. Since a proton hole has
minus the charge of a proton, the quadrupole moment for a single hole
is opposite to that of one proton:
 |
(14.36) |
In other words, the quadrupole moment for a single hole is predicted
to be positive. For 

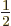 , a single proton also
means a single hole, so the quadrupole moment must, once more, be
zero. It has been found that the quadrupole moment changes linearly
with the odd number of protons, [31, p, 129]. Therefore for
shells with more than one proton and more than one hole, the
quadrupole moment is in between the one-proton and one-hole values.
It follows that the one-proton value provides an upper bound to the
magnitude of the quadrupole moment for any number of protons in the
shell.
, a single proton also
means a single hole, so the quadrupole moment must, once more, be
zero. It has been found that the quadrupole moment changes linearly
with the odd number of protons, [31, p, 129]. Therefore for
shells with more than one proton and more than one hole, the
quadrupole moment is in between the one-proton and one-hole values.
It follows that the one-proton value provides an upper bound to the
magnitude of the quadrupole moment for any number of protons in the
shell.
Since neutrons have no charge, even-odd nuclei would in the simplest
approximation have no quadrupole moment at all. However, consider the
odd neutron and the spherical remainder of the nucleus as a two-body
system going around their common center of gravity. In that picture,
the charged remainder of the nucleus will create a quadrupole moment.
The position vector of the remainder of the nucleus is about 1
 times shorter than that of the odd neutron, so quadratic lengths are a
factor 1
times shorter than that of the odd neutron, so quadratic lengths are a
factor 1
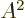 shorter. However, the nucleus has
shorter. However, the nucleus has 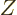 times as much
charge as a single proton. Therefore you expect nuclei with an odd
neutron to have about
times as much
charge as a single proton. Therefore you expect nuclei with an odd
neutron to have about 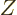

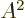 times the quadrupole moment of the
corresponding nucleus with an odd proton instead of an odd neutron.
For heavy nuclei, that would still be very much smaller than the
magnetic moment of a similar odd-even nucleus.
times the quadrupole moment of the
corresponding nucleus with an odd proton instead of an odd neutron.
For heavy nuclei, that would still be very much smaller than the
magnetic moment of a similar odd-even nucleus.
14.17.2.4 Draft: Values for deformed nuclei
For deformed nuclei, part of the angular momentum is due to rotation
of the nucleus as a whole. In particular, for the ground state
rotational band of deformed even-even nuclei, all angular momentum is
in rotation of the nucleus as a whole. This is orbital angular
momentum. Protons with orbital angular momentum produce a magnetic
dipole moment equal to their angular momentum, provided the dipole
moment is expressed in terms of the nuclear magneton 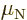 .
Uncharged neutrons do not produce a dipole moment from orbital angular
momentum. Therefore. the magnetic dipole moment of the nucleus is
about
.
Uncharged neutrons do not produce a dipole moment from orbital angular
momentum. Therefore. the magnetic dipole moment of the nucleus is
about
 |
(14.37) |
where the  -factor reflects the relative amount of the nuclear
angular momentum that belongs to the protons. This also works for
vibrational nuclei, since their angular momentum too is in global
motion of the nucleus.
-factor reflects the relative amount of the nuclear
angular momentum that belongs to the protons. This also works for
vibrational nuclei, since their angular momentum too is in global
motion of the nucleus.
If a rotational band has a minimum spin 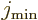 that is not zero,
the dipole moment is, [40, p. 392],
that is not zero,
the dipole moment is, [40, p. 392],
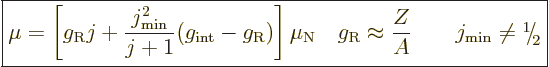 |
(14.38) |
where 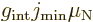 reflects an internal magnetic
dipole strength. If
reflects an internal magnetic
dipole strength. If 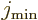

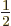 , the top of
the first ratio has an additional term that has a magnitude
proportional to
, the top of
the first ratio has an additional term that has a magnitude
proportional to 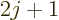 and alternates in sign.
and alternates in sign.
The quadrupole moment of deformed nuclei is typically many times
larger than that of a shell model one. According to the shell model,
all protons except at most one are in spherical orbits producing no
quadrupole moment. But if the nucleus is deformed, typically into
about the shape of some spheroid instead of a sphere, then all protons
contribute. Such a nucleus has a very large “intrinsic” quadrupole moment 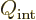 .
.
However, that intrinsic quadrupole moment is not the one measured.
For example, many heavy even-even nuclei have very distorted
intrinsic shapes but all even-even nuclei have a measured
quadrupole moment that is zero in their ground state. That is a pure
quantum effect. Consider the state in which the axis of the nucleus
is aligned with the  -direction. In that state a big quadrupole
moment would be observed due to the directional charge distribution.
But there are also states in which the nucleus is aligned with the
-direction. In that state a big quadrupole
moment would be observed due to the directional charge distribution.
But there are also states in which the nucleus is aligned with the
 -direction, the
-direction, the  -direction, and any other direction for that
matter. No big deal classically: you just grab hold of the nucleus
and measure its quadrupole moment. But quantum mechanics makes the
complete wave function a linear combination of all these different
possible orientations; in fact an equal combination of them by
symmetry. If all directions are equal, there is no directionality
left; the measured quadrupole moment is zero. Also, directionality
means angular momentum in quantum mechanics; if all directions are
equal the spin is zero.
-direction, and any other direction for that
matter. No big deal classically: you just grab hold of the nucleus
and measure its quadrupole moment. But quantum mechanics makes the
complete wave function a linear combination of all these different
possible orientations; in fact an equal combination of them by
symmetry. If all directions are equal, there is no directionality
left; the measured quadrupole moment is zero. Also, directionality
means angular momentum in quantum mechanics; if all directions are
equal the spin is zero. Grabbing hold
of the nucleus
means adding directionality, adding angular momentum. That creates an
excited state.
A simple known system that shows such effects is the hydrogen atom.
Classically the atom is just an electron and a proton at opposite
sides of their center of gravity. If they are both on the  -axis,
say, that system would have a nonzero quadrupole moment. But such a
state is not an exact energy eigenstate, far from it. It interacts
with states in which the direction of the connecting line is
different. By symmetry, the ground state is the one in which all
directions have the same probability. The atom has become spherically
symmetric. Still, the atom has not become intrinsically
spherically symmetric; the wave function is not of a form like
-axis,
say, that system would have a nonzero quadrupole moment. But such a
state is not an exact energy eigenstate, far from it. It interacts
with states in which the direction of the connecting line is
different. By symmetry, the ground state is the one in which all
directions have the same probability. The atom has become spherically
symmetric. Still, the atom has not become intrinsically
spherically symmetric; the wave function is not of a form like
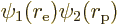 . The positions of
electron and proton are still correlated, {A.5}.
. The positions of
electron and proton are still correlated, {A.5}.
A model of a spheroidal nucleus produces the following relationship
between the intrinsic quadrupole moment and the one that is measured:
 |
(14.39) |
where 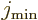 is the angular momentum of the nucleus when it is
not rotating. Derivations may be found in
[40] or [36]. It can be
seen that when the nucleus is not rotating, the measured quadrupole
moment is much smaller than the intrinsic one unless the angular
momentum is really large. When the nucleus gets additional rotational
angular momentum, the measured quadrupole moment decreases even more
and eventually ends up with the opposite sign.
is the angular momentum of the nucleus when it is
not rotating. Derivations may be found in
[40] or [36]. It can be
seen that when the nucleus is not rotating, the measured quadrupole
moment is much smaller than the intrinsic one unless the angular
momentum is really large. When the nucleus gets additional rotational
angular momentum, the measured quadrupole moment decreases even more
and eventually ends up with the opposite sign.
14.17.3 Draft: Magnetic moment data
Figure 14.42 shows ground state magnetic moments in units
of the nuclear magneton 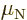 . Even-even nuclei do not have
magnetic moments in their ground state, so they are not shown. The
red and blue horizontal lines are the Schmidt values predicted by the
shell model. They differ in whether spin subtracts from or adds to
the net angular momentum
. Even-even nuclei do not have
magnetic moments in their ground state, so they are not shown. The
red and blue horizontal lines are the Schmidt values predicted by the
shell model. They differ in whether spin subtracts from or adds to
the net angular momentum  to produce the orbital momentum
to produce the orbital momentum
 . Red dots should be on the red lines, blue dots on the blue
lines. For black dots, no confident prediction of the orbital angular
momentum could be made. The values have an error of no more than
about 0.1
. Red dots should be on the red lines, blue dots on the blue
lines. For black dots, no confident prediction of the orbital angular
momentum could be made. The values have an error of no more than
about 0.1 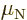 , based on a subjective evaluation of both
reported errors as well as differences between results obtained by
different studies for the same number. These differences are often
much larger than the reported errors for the individual numbers.
, based on a subjective evaluation of both
reported errors as well as differences between results obtained by
different studies for the same number. These differences are often
much larger than the reported errors for the individual numbers.
Figure 14.42:
Magnetic dipole moments of the ground-state nuclei.
[pdf]
 |
One good thing to say about it all is that the general magnitude is
well predicted. Few nuclei end up outside the Schmidt lines.
(Rhodium-103, a stable odd-even  nucleus, is a notable
exception.) Also, some nuclei are actually on their line. And the
others tend to at least be on the right side of the cloud. The bad
news is, of course, that the agreement is only qualitatively.
nucleus, is a notable
exception.) Also, some nuclei are actually on their line. And the
others tend to at least be on the right side of the cloud. The bad
news is, of course, that the agreement is only qualitatively.
The main excuses that are offered are:
-
1.
- The
 -factors
-factors  and
and 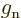 describe the
effectiveness of proton and neutron spins in generating magnetic
moments in free space. They may be reduced when these nucleons are
inside a nucleus. Indeed, it seems reasonable enough to assume that
the motion of the quarks that make up the protons and neutrons could
be affected if there are other quarks nearby. Reduction of the
describe the
effectiveness of proton and neutron spins in generating magnetic
moments in free space. They may be reduced when these nucleons are
inside a nucleus. Indeed, it seems reasonable enough to assume that
the motion of the quarks that make up the protons and neutrons could
be affected if there are other quarks nearby. Reduction of the
 -factors drives the Schmidt lines towards each other, and that
can clearly reduce the average errors. Unfortunately, different
nuclei would need different reductions to obtain quantitative
agreement.
-factors drives the Schmidt lines towards each other, and that
can clearly reduce the average errors. Unfortunately, different
nuclei would need different reductions to obtain quantitative
agreement.
-
2.
- Collective motion. If some of the angular momentum is into
collective motion, it tends to drift the magnetic moment towards
about
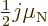 , compare (14.38). To compute
the effect requires the internal magnetic moment of the nucleus to
be known. For some nuclei, fairly good magnetic moments can be
obtained by using the Schmidt values for the internal magnetic
moment, [40, p. 393].
, compare (14.38). To compute
the effect requires the internal magnetic moment of the nucleus to
be known. For some nuclei, fairly good magnetic moments can be
obtained by using the Schmidt values for the internal magnetic
moment, [40, p. 393].
For odd-odd nuclei, the data average out to about 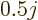 nuclear
magnetons, with a standard deviation of about one magneton. These
average values are shown as yellow lines in figure 14.42.
Interestingly enough, the average is like a collective rotation,
(14.37).
nuclear
magnetons, with a standard deviation of about one magneton. These
average values are shown as yellow lines in figure 14.42.
Interestingly enough, the average is like a collective rotation,
(14.37).
According to the shell model, two odd particles contribute to the spin
and magnetic moment of odd-odd nuclei. So they could have
significantly larger spins and magnetic moments than odd mass nuclei.
Note from the data in figure 14.42 that that just does not
happen.
Figure 14.43:
2 magnetic moment of even-even nuclei.
[pdf][con]
magnetic moment of even-even nuclei.
[pdf][con]
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(405,56...
...put(17,-12){\makebox(0,0)[bl]{2}}
}
\end{picture}}
\end{picture}
\end{figure}](img3366.gif) |
Even-even nuclei do not have magnetic moments in their ground state.
Figure 14.43 shows the magnetic moments of the first exited
2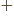 state of these nuclei. The values are in fairly good agreement
with the prediction (14.37) of collective motion that the
magnetic moment equals
state of these nuclei. The values are in fairly good agreement
with the prediction (14.37) of collective motion that the
magnetic moment equals 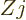

 nuclear magnetons. Bright green squares
are correct. Big deviations occur only near magic numbers. The
maximum error in the shown data is about a quarter of a nuclear
magneton, subjectively evaluated.
nuclear magnetons. Bright green squares
are correct. Big deviations occur only near magic numbers. The
maximum error in the shown data is about a quarter of a nuclear
magneton, subjectively evaluated.
14.17.4 Draft: Quadrupole moment data
If you love the shell model, you may want to skip this subsection. It
is going to get a beating.
Figure 14.44:
Electric quadrupole moment.
[pdf][con]
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(405,56...
...2.5,-.3){\makebox(0,0)[bl]{$<0$}}
}
\end{picture}}
\end{picture}
\end{figure}](img3368.gif) |
The prediction of the shell model is relatively straightforward. The
electric quadrupole moment of a single proton in an unfilled shell of
high angular momentum can quite well be ballparked as
where  is the nuclear radius computed from (14.9). This
value corresponds to the area of the square marked “a
proton’s” in the legend of figure 14.44. As
discussed in subsection 14.17.2.3, if there are more protons in
the shell, the magnitude is less, though the sign will eventually
reverse. If the angular momentum is not very high, the magnitude is
less. If there is no odd proton, the magnitude will be almost zero.
So, essentially all squares in figure 14.44 must be smaller,
most a lot smaller, and those on lines of even
is the nuclear radius computed from (14.9). This
value corresponds to the area of the square marked “a
proton’s” in the legend of figure 14.44. As
discussed in subsection 14.17.2.3, if there are more protons in
the shell, the magnitude is less, though the sign will eventually
reverse. If the angular momentum is not very high, the magnitude is
less. If there is no odd proton, the magnitude will be almost zero.
So, essentially all squares in figure 14.44 must be smaller,
most a lot smaller, and those on lines of even 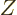 very much smaller,
than the single proton square in the legend...
very much smaller,
than the single proton square in the legend...
Well, you might be able to find a smaller square somewhere. For
example, the square for lithium-6, straight above doubly-magic
 , has about the right size and the
right color, blue. The data shown have a subjectively estimated error
of up to 40%, [sic], and the area of the squares gives the scaled
quadrupole moment. Nitrogen-14, straight below doubly-magic
, has about the right size and the
right color, blue. The data shown have a subjectively estimated error
of up to 40%, [sic], and the area of the squares gives the scaled
quadrupole moment. Nitrogen-14, straight below doubly-magic
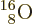 , has a suitably small square of
the right color, red. So does potassium-39 with one proton less than
doubly-magic
, has a suitably small square of
the right color, red. So does potassium-39 with one proton less than
doubly-magic 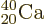 . Bismuth-209, with
one more proton than
. Bismuth-209, with
one more proton than 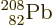 has a relatively
small square of the right color. Some nuclei on magic proton number
lines have quite small scaled quadrupole moments, though hardly almost
zero as they should. Nuclei one proton above magic proton numbers
tend to be of the right color, blue, as long as their squares are
small. Nuclei one proton below the magic proton numbers should be
red; however, promotion can mess that up.
has a relatively
small square of the right color. Some nuclei on magic proton number
lines have quite small scaled quadrupole moments, though hardly almost
zero as they should. Nuclei one proton above magic proton numbers
tend to be of the right color, blue, as long as their squares are
small. Nuclei one proton below the magic proton numbers should be
red; however, promotion can mess that up.
Back to reality. Note that many nuclei in the 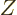
 82,
82, 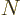
 82 wedge, and above
82 wedge, and above 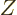
 82, as well as various other nuclei,
especially away from the stable line, have quadrupole moments that are
very many times larger than the ballpark for a single proton. That is
simply not possible unless many or all protons contribute to the
quadrupole moment. The odd-particle shell model picture of a
spherically symmetric nuclear core plus an odd proton, and maybe a
neutron, in nonspherical orbits hanging on is completely wrong for
these nuclei. These nuclei have a global shape that simply is not
spherical. And because the shell model was derived based on a
spherical potential, its results are invalid for these nuclei. They
are the deformed nuclei that also showed up in figures 14.19
and 14.22. It is the quadrupole moment that shows that it
was not just an empty excuse to exclude these nuclei in shell model
comparisons. The measured quadrupole moments show without a shadow of
a doubt that the shell model cannot be valid.
82, as well as various other nuclei,
especially away from the stable line, have quadrupole moments that are
very many times larger than the ballpark for a single proton. That is
simply not possible unless many or all protons contribute to the
quadrupole moment. The odd-particle shell model picture of a
spherically symmetric nuclear core plus an odd proton, and maybe a
neutron, in nonspherical orbits hanging on is completely wrong for
these nuclei. These nuclei have a global shape that simply is not
spherical. And because the shell model was derived based on a
spherical potential, its results are invalid for these nuclei. They
are the deformed nuclei that also showed up in figures 14.19
and 14.22. It is the quadrupole moment that shows that it
was not just an empty excuse to exclude these nuclei in shell model
comparisons. The measured quadrupole moments show without a shadow of
a doubt that the shell model cannot be valid.
You might however wonder about the apparently large amount in random
scatter in the quadrupole moments of these nuclei. Does the amount of
deformation vary that randomly? Before that can be answered, a
correction to the data must be applied. Measured quadrupole moments
of a deformed nucleus are often much too small for the actual nuclear
deformation. The reason is uncertainty in the angular orientation of
these nuclei. In particular, nuclei with spin zero have complete
uncertainty in orientation. Such nuclei have zero measured quadrupole
moment regardless how big the deformation of the nucleus is. Nuclei
with spin one-half still have enough uncertainty in orientation to
measure as zero.
Figure 14.45:
Electric
quadrupole moment corrected for spin.
[pdf][con]
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(405,56...
....5,-0.3){\makebox(0,0)[bl]{$<0$}}
}
\end{picture}}
\end{picture}
\end{figure}](img3372.gif) |
Figure 14.45 shows what happens if you try to estimate the
intrinsic
quadrupole moment of the nuclei in absence
of uncertainty in angular orientation. For nuclei whose spin is at
least one, the estimate was made based on the measured value using
(14.39), with both 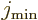 and
and  equal to the
spin. This assumes that the intrinsic shape is roughly spheroidal.
For shell-model nuclei, this also roughly corrects for the spin
effect, though it overcorrects to some extent for nuclei of low spin.
equal to the
spin. This assumes that the intrinsic shape is roughly spheroidal.
For shell-model nuclei, this also roughly corrects for the spin
effect, though it overcorrects to some extent for nuclei of low spin.
To estimate the intrinsic quadrupole moment of nuclei with zero ground
state spin, including all even-even nuclei, the quadrupole moment of
the lowest excited 2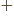 state was used, if it had been measured. For
spin one-half the lowest
state was used, if it had been measured. For
spin one-half the lowest  state was used. In either case,
state was used. In either case,
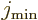 was taken to be the spin of the ground state and
was taken to be the spin of the ground state and  that of the excited state. Regrettably, these estimates do not make
much sense if the nucleus is not a rotating one.
that of the excited state. Regrettably, these estimates do not make
much sense if the nucleus is not a rotating one.
Note in figure 14.45 how much more uniform the squares in the
regions of deformed nuclei have become. And that the squares of
nuclei of spin zero and one-half have similar sizes. These nuclei
were not really more spherical; it was just hidden from experiments.
The observed intrinsic quadrupole moments in the regions of deformed
nuclei correspond to roughly 20% radial deviation from the spherical
value. Clearly, that means quite a large change in shape.
It may be noted that figure 14.44 leaves out magnesium-23,
whose reported quadrupole moment of 1.25 barn is far larger that that
of similar nuclei. If this value is correct, clearly magnesium-23
must be a halo nucleus with two protons outside a neon-21 core.
![]()
![]()
![]() ,
,![]()
![]() .
.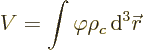
![]() .
.![]()
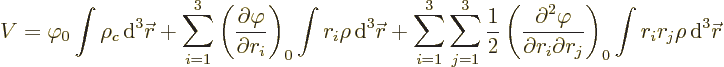
![]() .
.![]() -
-![]()
![]()
![]()
![]() ,
,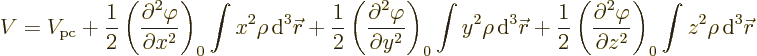
![]() ,
,![]() ,
,![]()
![]() .
.![]()
![]() -
-
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() .
.![]() ,
,![]()
![]()
![]()
![]() -
-![]()
![]()
![]() .
.![]() -
-![]()
![]()
![]()
![]() .
.![]()
![]() .
.![]() -
-![]() .
.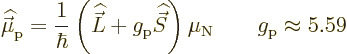
![\begin{displaymath}
{\skew 4\widehat{\skew{-.5}\vec\mu}}= \frac{1}{\hbar}
\lef...
...}^A g_{\rm n} {\skew 6\widehat{\vec S}}_i
\right] \mu_{\rm N}
\end{displaymath}](img3332.gif)
![]()
![]() -
-![]()
![]() ,
,![]()
![]() -
-![]() ?
?![]() ?
?![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]() ,
,![]()
![]()
![]() .
.![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]() ,
,![]()
![]() ,
,![]()
![]() :
: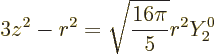
![]()
![]()
![]() .
.![]()
![]()
![]() .
.![]()
![]() .
.![]()
![]() .
.![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]() .
.![]() -
-![]() -
-![]() -
-![]() -
-![]() .
.![]() .
.![]()
![]() .
.![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]() ,
,![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()