|
|
|
|
|
Next: 7.11 Almost Classical Motion |
|
This section gives a full description of the motion of a particle
according to quantum mechanics. It will be assumed that the particle
is in free space, so that the potential energy is zero. In addition,
to keep the analysis concise and the results easy to graph, it will be
assumed that the motion is only in the ![]() -
-
One thing that the analysis will show is how limiting the uncertainty
in both momentum and position produces the various features of
classical Newtonian motion. It may be recalled that in Newtonian
motion through free space, the linear momentum ![]()
![]()
![]()
![]()
![]() ,
,
As discussed in section 7.1, the unsteady evolution of a
quantum system may be determined by finding the eigenfunctions of the
Hamiltonian and giving them coefficients that are proportional to
![]() .
.
For a free particle, there is only kinetic energy, so in one dimension
the Hamiltonian eigenvalue problem is:
| (7.56) |
Note that ![]()
![]() .
.![]()
The energy eigenfunction above is really the same as the eigenfunction
of the ![]() -
-![]()
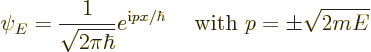 |
(7.57) |
As shown by (7.55) in the previous section, combinations of
momentum eigenfunctions take the form of an integral rather than a
sum. In the one-dimensional case that integral is:
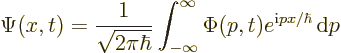
Whether a sum or an integral, the Schrödinger equation still requires that
the coefficient of each energy eigenfunction varies in time
proportional to ![]() .
.![]() ,
,![]()
![]()
![]()
![]()
![]() ,
,
Key Points
- In free space, momentum eigenfunctions are also energy eigenfunctions.
- The one-dimensional wave function for a particle in free space is given by (7.58).
- The function
is still to be chosen to produce whatever physical situation is to be described.
Before trying to interpret the complete obtained solution
(7.58) for the wave function of a particle in free space, it
is instructive first to have a look at the component solutions,
defined by
| (7.59) |
In figure 7.11, the real part of the wave (in other words, the cosine), is sketched as the red curve; also the magnitude of the wave (which is unity) is shown as the top black line, and minus the magnitude is drawn as the bottom black line.
The black lines enclose the real part of the wave, and will be called
the envelope.
Since their vertical separation is twice
the magnitude of the wave function, the vertical separation between
the black lines at a point is a measure for the probability of finding
the particle near that point.
The constant separation between the black lines shows that there is absolutely no localization of the particle to any particular region. The particle is equally likely to be found at every point in the infinite range. This also graphically demonstrates the normalization problem of the momentum eigenfunctions discussed in the previous section: the total probability of finding the particle just keeps getting bigger and bigger, the larger the range you look in. So there is no way that the total probability of finding the particle can be limited to one as it should be.
The reason for the complete lack of localization is the fact that the
component wave solutions have an exact momentum ![]() .
.
There is another funny thing about the component waves: when plotted
for different times, it is seen that the real part of the wave moves
towards the right with a speed ![]()
![]()
![]()
![]()
![]() ,
,
This is unexpected, because classically the particle moves with speed
![]() ,
,![]() .
.
Key Points
- Component waves provide no localization of the particle at all.
- Their real part is a moving cosine. Similarly their imaginary part is a moving sine.
- The speed of motion of the cosine or sine is half the speed of a classical particle with that momentum.
- This speed is called the phase speed and is not relevant physically.
As Heisenberg’s principle indicates, in order to get some
localization of the position of a particle, some uncertainty must be
allowed in momentum. That means that you must take the initial
momentum space wave function ![]()
![]() .
.wave packet
.
The wave function for a typical wave packet is sketched in figure 7.13. The red line is again the real part of the wave function, and the black lines are the envelope enclosing the wave; they equal plus and minus the magnitude of the wave function.
 |
The vertical separation between the black lines is again a measure of the probability of finding the particle near that location. It is seen that the possible locations of the particle are now restricted to a finite region, the region in which the vertical distance between the black lines is nonzero.
If the envelope changes location with time, and it does, then so does the region where the particle can be found. This then finally is the correct picture of motion in quantum mechanics: the region in which the particle can be found propagates through space.
The limiting case of the motion of a macroscopic Newtonian point mass can now be better understood. As noted in section 7.2.1, for such a particle the uncertainty in position is negligible. The wave packet in which the particle can be found, as sketched in figure 7.13, is so small that it can be considered to be a point. To that approximation the particle then has a point position, which is the normal classical description.
The classical description also requires that the particle moves with velocity ![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
That the envelope does indeed move at speed ![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
the
momentum ![]() .
.
Key Points
- A wave packet is a combination of waves with about the same momentum.
- Combining waves into wave packets can provide localization of particles.
- The envelope of the wave packet shows the region where the particle is likely to be found.
- This region propagates with the classical particle velocity.
As the previous subsection explained, particle motion in classical mechanics is equivalent to the motion of wave packets in quantum mechanics. Motion of a wave packet implies that the region in which the particle can be found changes position.
Motion of wave packets is not just important for understanding where particles in free space end up. It is also critical for the quantum mechanics of for example solids, in which electrons, photons, and phonons (quanta of crystal vibrations) move around in an environment that is cluttered with other particles. And it is also of great importance in classical applications, such as acoustics in solids and fluids, water waves, stability theory of flows, electromagnetodynamics, etcetera. This section explains how wave packets move in such more general systems. Only the one-dimensional case will be considered, but the generalization to three dimensions is straightforward.
The systems of interest have component wave solutions of the general
form:
For a particle in free space according to the previous subsection:
Regardless of what kind of system it is, the relationship between the
frequency and the wave number is called the
Since the waves are of the form
![]() ,
,![]()
![]()
![]()
However, as noted in the previous subsection, wave packets do not
normally move with the phase velocity. The velocity that they do move
with is called the group velocity.
For a particle in
free space, you can infer that the group velocity is the same as the
classical velocity from Ehrenfest's theorem, but that does not work
for more general systems. The approach will therefore be to simply
define the group velocity as
Wave packets are combinations of component waves, and the most general
combination of waves takes the form
To describe the motion of wave packets is not quite as straightforward as it may seem: the envelope of a wave packet extends over a finite region, and different points on it actually move at somewhat different speeds. So what do you take as the point that defines the motion if you want to be precise? There is a trick here: consider very long times. For large times, the propagation distance is so large that it dwarfs the ambiguity about what point to take as the position of the envelope.
Finding the wave function ![]()
![]()
![]()
![]()
![]()
![]() .
.
thegroup velocity.
It is not just possible to say where the wave function is nonzero at
large times. It is also possible to write a complete approximate
wave function for large times:

While this precise expression may not be that important, it is
interesting to note that ![]()
![]() .
.![]()
![]()
![]()
One other interesting feature may be deduced from the above expression
for ![]() .
.![]()
![]() .
.
For the particle in free space, the result for the large time
wave function can be written out further to give
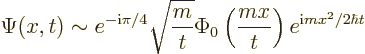
In a typical true quantum mechanics case, ![]()
![]() .
.![]()
![]()
Key Points
- Component waves have the generic form
.
- The constant
is the wave number.
- The constant
is the angular frequency.
- The relation between
and is called the dispersion relation.
- The phase velocity is
It describes how fast the wave moves. .
- The group velocity is
It describes how fast wave packets move. .
- Relatively simple expressions exist for the wave function of wave packets at large times.
One important application of group velocity is the motion of conduction electrons through crystalline solids. This subsection discusses it.
Conduction electrons in solids must move around the atoms that make up the solid. You cannot just forget about these atoms in discussing the motion of the conduction electrons. Even semi-classically speaking, the electrons in a solid move in a roller-coaster ride around the atoms. Any external force on the electrons is on top of the large forces that the crystal already exerts. So it is simply wrong to say that the external force gives mass times acceleration of the electrons. Only the total force would do that.
Typically, on a microscopic scale the solid is crystalline; in other words, the atoms are arranged in a periodic pattern. That means that the forces on the electrons have a periodic nature. As usual, any direct interactions between particles will be ignored as too complex to analyze. Therefore, it will be assumed that the potential energy seen by an electron is a given periodic function of position.
It will also again be assumed that the motion is one-dimensional. In
that case the energy eigenfunctions are determined from a
one-dimensional Hamiltonian eigenvalue problem of the form
Three-dimensional energy eigenfunctions may be found as products of
one-dimensional ones; compare chapter 3.5.8. Unfortunately
however, that only works here if the three-dimensional potential is
some sum of one-dimensional ones, as in
The energy eigenfunction solutions to (7.65) take the form
of Bloch waves:
The reason that the energy eigenfunctions take the form of Bloch waves
is not that difficult to understand. It is a consequence of the fact
that commuting operators have common eigenfunctions, chapter
4.5.1. Consider the “translation operator” ![]()
![]() .
.![]()
![]() .
.![]()
![]() .
.![]()
If the crystal is infinite in size, the wave number ![]()
![]()
To understand what the Bloch form means for the electron motion, first
consider the case that the periodic factor ![]()
![]()
![]() .
.
Even if there is a nontrivial crystal potential, the so-called
“crystal momentum” is still defined as:
Instead you can get the propagation velocity by differentiating the
energy with respect to the crystal momentum, {D.45}:
One conclusion that can be drawn is that electrons in an ideal crystal
keep moving with the same speed for all times like they do in free
space. They do not get scattered at all. The reason is that energy
eigenfunctions are stationary. Each eigenfunction corresponds to a
single value of ![]()
![]()
This perfectly organized motion of electrons through crystals is quite surprising. If you make up a classical picture of an electron moving through a crystal, you would expect that the electron would pretty much bounce off every atom it encountered. It would then perform a drunkard’s walk from atom to atom. That would really slow down electrical conduction. But it does not happen. And indeed, experimentally electrons in metals may move past many thousands of atoms without getting scattered. In very pure copper at very low cryogenic temperatures electrons may even move past many millions of atoms before getting scattered.
Note that a total lack of scattering only applies to truly ideal crystals. Electrons can still get scattered by impurities or other crystal defects. More importantly, at normal temperatures the atoms in the crystal are not exactly in their right positions due to thermal motion. That too can scatter electrons. In quantum terms, the electrons then collide with the phonons of the crystal vibrations. The details are too complex to be treated here, but it explains why metals conduct much better still at cryogenic temperatures than at room temperature.
The next question is how does the propagation velocity of the electron
change if an external force ![]()
![]()
However, since the velocity is not just the crystal momentum divided
by the mass, you cannot convert the left hand side to the usual mass
times acceleration. The acceleration is instead, using the chain rule
of differentiation,
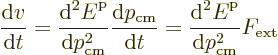
But physicists still like to think of the effect of force as mass
times acceleration of the electrons. So they cheat. They ignore the
true mass of the electron. Instead they simply define a new “effective mass” for the electron so that the external force
equals that effective mass times the acceleration:
Unfortunately, the effective mass is often a completely different
number than the true mass of the electron. Indeed, it is quite
possible for this mass
to become negative for some
range of wave numbers. Physically that means that if you put a force
on the electron that pushes it one way, it will accelerate in the
opposite direction! That can really happen. It is a consequence of
the wave nature of quantum mechanics. Waves in crystals can be
reflected just like electromagnetic waves can, and a force on the
electron may move it towards stronger reflection.
For electrons near the bottom of the conduction band, the effective
mass idea may be a bit more intuitive. At the bottom of the
conduction band, the energy has a minimum. From calculus, if the
energy ![]()
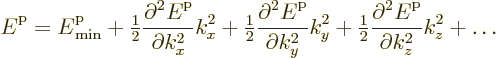
In this case the effective masses are indeed positive, since second derivatives must be positive near a minimum. These electrons act much like classical particles. They move in the right direction if you put a force on them. Unfortunately, the effective masses are not necessarily similar to the true electron mass, or even the same in each direction.
For the effective mass of the holes at the top of a valence band
things get much messier still. For typical semiconductors, the energy
no longer behaves as an analytic function, even though the energy in a
specific direction continues to vary quadratically with the magnitude
of the wave number. So the Taylor series is no longer valid. You
then end up with such animals as heavy holes,
light holes,” and “split-off holes.
Such
effects will be ignored in this book.
Key Points
- The energy eigenfunctions for periodic potentials take the form of Bloch waves, involving a wave number
.
- The crystal momentum is defined as
.
- The first derivative of the electron energy with respect to the crystal momentum gives the propagation velocity.
- The second derivative of the electron energy with respect to the crystal momentum gives the reciprocal of the effective mass of the electron.