|
|
|
|
|
Next: A.43 Classical vibrating drop |
|
The purpose of this addendum is to examine the nature of nuclear
forces somewhat closer. The forces will be modeled using the
meson exchange
idea. This idea illustrates one
primary way that physicists cope with the fact that nuclei are too
complex to describe exactly.
As pointed out in chapter 7.5.2, the fundamental forces of nature between elementary particles are due to the exchange of bosons between these particles. In those terms, nuclei consist of quarks. The exchange of gluons between these quarks produces the so-called color force. It is that force that holds nuclei together. Unfortunately, describing that mathematically is not a practical proposition. Quantum chromedynamics is prohibitively difficult.
But you will never find quarks or gluons in isolation. Quarks and
their gluons are always confined inside colorless
combinations of two or three quarks. (To be painstakingly honest,
there might be more exotic colorless combinations of quarks and gluons
than that. But their energy should be too high to worry about here.)
What is observed physically at the time of writing, 2012, are groups
of three quarks, (baryons), three antiquarks, (antibaryons), and a
quark and an antiquark (mesons). An easier description of nuclear
forces can be based on these groups of quarks.
In this picture, nuclei can be taken to consist of nucleons. A
nucleon consists of a group of three quarks, so it is a baryon. There
are two types of nucleons: protons and neutrons. A proton contains
two up
quarks, at electric charge ![]()
down
quark, at ![]() .
.![]()
![]() .
.![]()
For both protons and neutrons, the group of three quarks is in its
ground state, much like a helium atom is normally in its ground state.
Like single quarks, nucleons are fermions with spin equal to
![]() .
.
Protons and neutrons combine together into nuclei. However, the protons in nuclei repel each other because of their electric charges. So there must be some compensating force that keeps the nucleons together anyway. This force is what is called the “nuclear force.” The question in this addendum is how this nuclear force can be described. Its physical cause is still the force due to the exchange of gluons between quarks. But its mathematical description is going to be different. The reason is that by definition the nuclear force is a net force on nucleons, i.e. on groups of quarks. And it is assumed to depend on the average positions, and possibly momenta, of these groups of quarks.
Note that there is some approximation involved here. Exactly speaking, the nuclear forces should depend on the positions of the individual quarks in the nucleons, not just on their average position. That is a concern when two nucleons get very close together. For one, then the distinction between the two separate groups of quarks must blur. Nucleons do repel one another strongly at very close distances, much like atoms do due to Pauli repulsion, chapter 5.10. But still their quantum uncertainty in position creates a probability for them to be very close together. Fortunately, typical energy levels in normal nuclear physics are low enough that this is not believed to be a dominating effect. Indeed, the models discussed here are known to work very well at larger nucleon spacings. For smaller nucleon spacing however, they become much more complex, and their accuracy much more uncertain. And that happens well before the nucleons start intruding significantly on each others space. Little in life is ideal, isn’t it?
In a particle exchange explanation of the nuclear force, roughly
speaking nucleons have to pop up
particles that other
nucleons then absorb and vice-versa. The first question is what these
particles would be. As already mentioned, only colorless combinations
of quarks and their gluons are observed in isolation. Therefore only
such colorless combinations can be expected to be able to readily
bridge the gap between nucleons that are relatively far apart. The
lowest energy of these colorless combinations are the easiest to pop
up. And that are the pions; a pion is a meson consisting of a quark
and antiquark pair in its ground state.
There are three types of pions. The ![]()
![]() .
.![]()
![]()
![]() ,
,![]()
![]()
![]()
![]() .
.![]()
![]() .
.![]()
Pions are bosons of zero spin and negative intrinsic parity. The negative parity is due to the antiquark, and zero spin is due to the fact that in pions the quark and antiquark align their spins in opposite directions in a singlet state, chapter 5.5.6.
These pions are the most important particles that protons and neutrons exchange. The first question is then of course where they come from. How is it possible that pions just appear out of nothing? Well, it is possible due to a mixture of special relativity and the uncertainty inherent in quantum mechanics.
The creation of particles out of energy is allowed by special
relativity. As discussed in chapter 1.1.2, special
relativity gives the energy ![]()
Quantum mechanics replaces the momentum ![]()
![]()
![]()
![]()
![]() .
.
Now consider first a single nucleon located at the origin. Supposedly
this nucleon can pop up a pion. But where would the nucleon get the
135 MeV or more of energy? Surely, if there was a probability of
actually finding a 135 MeV pion well away from the nucleon, it would
violate energy conservation. But remarkably, despite the positive
pion rest mass energy, the Klein-Gordon equation has a simple solution
where the total pion energy ![]()
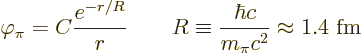
tunnels outof the nucleon, chapter 7.12.2.
To check the above solution, just plug it in the Klein-Gordon equation
(A.260) with ![]()
![]()
![]()
![]()
![]()
Now assume that the nucleon does indeed manage to create a pion field
around itself. A field that acts as a potential ![]()
![]()
![]()
![]()
![]()
![]()
Actually, despite the fact that it works for electromagnetics, the zero-energy wave function above does not quite give the right form for a pion potential. But it does give the general idea. The correct potential is discussed in the next subsections. This subsection will stick with the form above as qualitatively OK.
Now consider a second nucleon. This nucleon will of course also create a pion potential. That is just like if it was all by itself. But in addition, it will interact with the pion potential created by the first nucleon. So there will be an energy of interaction between the nucleons. Taking another cue from electromagnetics, this energy should presumably be proportional to the potential that the first nucleon creates at the position of the second nucleon.
That idea then gives the interaction energy between two nucleons as
The Yukawa potential is attractive. This is in contrast to the
Coulomb potential, which is repulsive between like charges. The best
physical explanation for the difference may be the analysis in
{A.22}, in particular {A.22.5}. (There are many
other explanations
that derive the difference using an
electromagnetic Hamiltonian or Lagrangian that already has the
difference build in. But a derivation is not an explanation.)
Note the exponential in the Yukawa potential. It will make the
potential negligibly small as soon as the distance ![]()
![]() .
.![]()
![]()
Actually, at the time that Yukawa did his work, the pion was unknown. But the range of the nuclear force was fairly well established. So Yukawa really predicted the existence, as well as the mass of the pion, a then unknown particle! After a long and frustrating search, this particle was eventually discovered in cosmic rays.
The Yukawa potential also explained why heavy nuclei are unstable. Suppose that you keep stuffing nucleons, and in particular protons, into a nucleus. Because of the exponential in the Yukawa potential, the nuclear force is very short range. It is largely gone beyond distances of a couple of fm. So a proton gets pulled into the nucleus only by the nucleons in its immediate vicinity. But the Coulomb repulsion between protons does not have the exponential decay. So the same proton gets pushed out of the nucleus by protons from all over the nucleus. If the nucleus is big enough, the pushers simply have to win because of their much larger numbers.
Putting a lot of neutrons in the nucleus can help, because they produce nucleon attraction and no Coulomb repulsion. But neutrons by themselves are unstable. Put too many neutrons in a nucleus, and they will turn into protons by beta decay. Obviously, that defeats the purpose. As a result, beyond a certain size, the nucleus is going to fall apart whatever you do.
You can see why Yukawa would end up with the Nobel prize in physics.
The Yukawa potential energy (A.261) described in the previous section is not quite right yet. It does not give the true nuclear force between two nucleons produced by pion exchange.
In a more careful analysis, the potential energy depends critically on
the properties of the exchanged particle. See the next subsection for
an explanation of that. For a pion, the relevant properties are that
it has zero spin and negative parity. Taking that into account
produces the so-called “one-pion exchange potential” energy or “OPEP” for short:
Finally the dot product ![]()
isospin
of the nucleons. Isospin will be
discussed in chapter 14.18. There it will be explained that
it has nothing to do with spin. Instead isospin is related to nucleon
type. In particular, if both nucleons involved are protons, or if
both are neutrons, then ![]()
![]()
If one nucleon is a proton and the other a neutron, like in the
deuteron, the value of ![]()
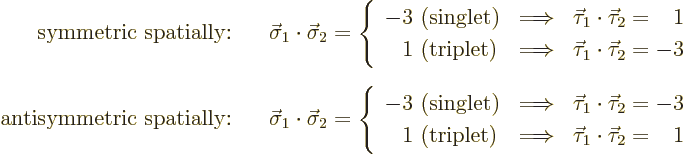
For the deuteron, as well as for the hypothetical diproton and
dineutron, the spatial state is symmetric under nucleon exchange.
That is as you would expect for a ground state,
{A.8} and {A.9}. It then follows
from the above values that the first,
![]() ,
,
The second, ![]() ,
,
The deuteron however can be in the triplet spin state. In that case
the tensor potential is not zero. To be sure, the tensor potential
does average out to zero over all directions of ![]() .
.![]()
![]()
![]()
Of course, that also depends on ![]() .
.![]()
![]()
![]() -
-![]()
The purpose of this subsection is to explain the OPEP potential between nucleons as given in the previous subsection physically.
Note that the objective is not to give a rigorous derivation of the OPEP potential using advanced quantum field theory. Physicists presumably already got the OPEP right. They better, because it is a standard part of current nuclear potentials. The explanations here will be based on simple physical assumptions. They follow the derivation of the Koulomb potential in {A.22.1}. That derivation was classical, although a simple quantum field version can be found in {A.22.3}. Note that the original Yukawa derivation was classical too. It was still worth a Nobel prize.
The arguments here are loosely based on [16, p. 282-288]. However, often the assumptions made in that reference seem quite arbitrary. To avoid that, the exposition below makes much more liberal use of quantum ideas. After all, in final analysis the classical field is just a reflection of underlying quantum mechanics. Hopefully the quantum arguments will show much more compellingly that things just have to be the way they are.
First of all, like in the first subsection it will be assumed that every nucleon can generate a pion potential. Other nucleons can observe that potential and interact with it, producing forces between the nucleons involved.
The net pion potential produced by all the nucleons will be called
![]() .
.![]()
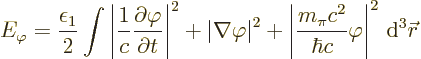
(Do note that there are some qualifications to the statement that the above integral gives the correct energy in an electrostatic field. The electromagnetic field is quite tricky because, unlike the pion, the photon wave function is a relativistic four-vector. See {A.22} for more. But at the very least, the integral above gives the correct expression for the effective energy in the electrostatic field.)
Finally it will be assumed that there is an interaction energy between
the observable pion field and the nucleons. But the precise
expression for that interaction energy is not yet obvious. Only a
generic expression can reasonably be postulated at this stage. In
particular, it will be postulated that the interaction energy of the
pion field with an arbitrary nucleon numbered ![]()
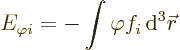
It still needs to be figured out what is the appropriate form of this
interaction factor. But it will be assumed that it involves the wave
function ![]()
![]()
![]()
local,
rather than long
range; it occurs at the location of the nucleon. One motivation for
this assumption is that long-range interactions are just bound to
produce problems with special relativity.
It will further be assumed that the wave function of each nucleon ![]()
![]() .
.![]()
![]()
The ground state is the state in which the combined pion field and
interaction energy is minimal. To find the properties of that state
requires variational calculus. This is worked out in considerable
detail in {A.22.1} and {A.2}. (While those
derivations do not include the ![]()
The variational analysis further shows that the energy of interaction
between a nucleon numbered ![]()
![]()
The big question remains, what exactly is the interaction factor ![]()
![]() ?
?
fg” stands for “first-guessand
Given the above first-guess interaction factor, according to
(A.263) a nucleon ![]()
The above potential is spherically symmetric; it is the same in all
directions. (That is true even if the nucleon wave function is not
spherically symmetric. The wave function is only nonzero very close
to ![]() ,
,
The interaction energy with a second nucleon ![]()
![]()
![]() ,
,![]()
![]() .
.![]() .
.![]()
![]() .
.
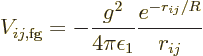
The Yukawa potential would be appropriate for a field of spinless pions with positive intrinsic parity. And except for the sign problem mentioned in the first subsection, it also gives the correct Coulomb potential energy in electrostatics.
Unfortunately, as noted in the first subsection, the pion has negative
intrinsic parity, not positive. And that is a problem. Imagine for a
second that a nucleon pops up a pion. The nucleon has positive
parity. However, the pion that pops up has negative intrinsic parity.
And parity is preserved, chapter 7.3. If the intrinsic
parity of the pion is negative, its orbital parity must be negative
too to maintain a positive combined system parity, chapter
7.4.2. Negative orbital parity means that the pion wave
function ![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
(Note that this argument blurs the distinction between a pion wave
function ![]()
![]() .
.
(You might also, correctly, object to the inaccurate picture that the nucleon pops up a pion. The ground state of the nucleon-pions system is a state of definite energy. Energy states are stationary, chapter 7.1.4. However, in energy states the complete nucleon-pions system should have definite angular momentum and parity, chapter 7.3. That is just like nuclei in energy states have definite angular momentum and parity, chapter 14.1. The term in the nucleon-pions system wave function in which there is just the nucleon, with no pions, already sets the angular momentum and parity. A different term in the system wave function, in particular one in which there is a pion in a state of definite angular momentum and parity, cannot have different angular momentum or parity. Otherwise angular momentum and parity would have uncertainty.)
So how to fix this? Suppose that you differentiate the first-guess
potential (A.265) with respect to, say, ![]() .
.![]()
According to (A.263), the first guess potential satisfies
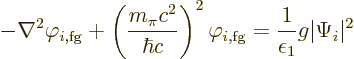
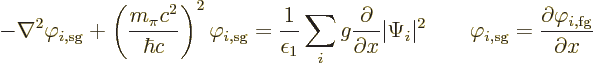
There are a couple of new problems. First of all, this potential now
has orbital angular momentum. If you check out the spherical
harmonics in table 4.3, you see that a spherically symmetric
wave function has no orbital angular momentum. But the factor ![]()
So where does this angular momentum come from? Angular momentum
should be preserved. The pion itself has no spin. So its orbital
angular momentum will have to come from the half unit of nucleon spin.
Indeed it is possible for half a unit of nucleon spin, ![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]() ,
,
But consider also the angular momentum in the ![]() -
-![]()
![]() -
-![]()
![]() -
-![]() .
.![]()
![]() ,
,![]()
![]() .
.![]() -
-
In quantum terms, how does that happen? Consider the scaled nucleon
![]()
![]()
spin-up
state with ![]()
![]() ,
,![]()
![]()
![]() .
.![]() .
.![]()
![]()
![]()
![]()
![]()
The second problem has to do with the original notion of
differentiating the spherically symmetric potential with respect to
![]() .
.![]()
![]()
![]() -
-![]()
![]()
Now dot products are the same regardless of how the coordinate system
is oriented. That then suggests how both problems above can be solved
at the same time. In the first-guess interaction factor, add the dot
product between the scaled nucleon spin ![]()
![]() .
.
![\begin{displaymath}
f_{i,\rm tg} = g R \vec\sigma_i\cdot\nabla_i \vert\Psi_i\ve...
...ma_z \frac{\partial}{\partial z_i}
\right] \vert\Psi_i\vert^2
\end{displaymath}](img5544.gif)
Time for a reality check. Consider a nucleon in the spin-up state.
If the mesic charge
![]()
![]()
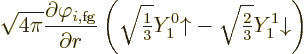
So the third guess seems pretty good. But there is one more thing.
Recall that there are three different pions, with different charges,
So you would expect that there are really three different functions
![]() ,
,![]()
Note that charge is preserved. If a proton pops up a positively
charged ![]()
![]() ,
,![]()
So, it is necessary to describe change of nucleon type. Physicists do
that in a very weird way; they pattern the mathematics on that of
spin, chapter 14.18. First a completely abstract
123
coordinate system is introduced. If a nucleon is
a proton, then it is said that the nucleon has a component ![]()
![]()
Compare that with spin. If a nucleon is spin-up, it has a spin
component ![]()
![]() -
-![]()
![]() -
-
Now recall from above that the operators ![]()
![]()
![]() -
-![]()
![]()
![]() ,
,![]() ,
,
Of course, all this may seem an extremely round-about way of doing
something simple: define operators that flip over nucleon type. And
normally it really would be. But if it is assumed that nuclear forces
are charge-independent, (which is a reasonable approximation), things
change. In that case it turns out that the physics must remain the
same under rotations of this abstract 123-coordinate system. And that
requirement can again be met by forming a dot product, this time
between ![]()
![]()
![]()
That idea then gives the final expression for the functions
![]() :
:
![\begin{displaymath}
\vec f_i = g R \vec\tau_i\;\;\vec\sigma_i\cdot\nabla_i \ver...
...ma_z \frac{\partial}{\partial z_i}
\right] \vert\Psi_i\vert^2
\end{displaymath}](img5551.gif)
Now it is just a matter of working out the final potential. Do one
thing at a time. Recall first the effect of the ![]() -
-![]() -
-
![\begin{displaymath}
\frac{gR}{4\pi\epsilon_1} \frac{{\rm d}e^{-r/R}/r}{{\rm d}r...
...silon_1}
\left[\frac{1}{Rr^2}+\frac{1}{r^3}\right] e^{-r/R} x
\end{displaymath}](img5555.gif)
![\begin{displaymath}
\varphi_i({\skew0\vec r}) = - \frac{gR}{4\pi\epsilon_1} \ve...
...+\frac{1}{r^3}\right] e^{-r/R} {\skew0\vec r}\cdot\vec\sigma_i
\end{displaymath}](img5556.gif)
Now the interaction potential with another nucleon follows from
(A.264). But here you need to be careful. The integral will
involve terms like
![\begin{displaymath}
\mbox{[some constant] }
\int \varphi_i({\skew0\vec r}) \fr...
...tial \vert\Psi_j\vert^2}{\partial x} {\,\rm d}^3{\skew0\vec r}
\end{displaymath}](img5557.gif)
Differentating the potential is a bit of a mess, but straightforward.
Then the potential becomes
![\begin{displaymath}
V_{ij} \sim \frac{g^2}{12\pi\epsilon_1R} \;\, \vec\tau_i\cd...
...t\vec\sigma_j + S_{ij} V_{\rm {T}} \Big]
\frac{e^{-r/R}}{r/R}
\end{displaymath}](img5558.gif)
Unfortunately, the nuclear force is not just a matter of the exchange of single pions. While the OPEP works very well at nucleon distances above 3 fm, at shorter ranges other processes become important.
The most important range is the one of the primary nucleon attractions.
Conventionally, this range is ballparked as nucleon distances in the
range 1 ![]()
![]()
Two-pion exchanges are much more difficult to crunch out than one-pion
ones. In addition, it turns out that straightforward two-pion exchanges
are not enough, [[3]]. The interactions also have to
include various so-called resonances.
Resonances are extremely short-lived excited states of baryons and
mesons. They decay through the strong force, which typically takes on
the order of 1![]()
The lowest energy excited state for nucleons is a set of resonances
called the “delta particles,” ![]() ,
,![]() ,
,![]() ,
,![]() .
.![]() .
.![]()
![]() ,
,![]()
![]()
![]()
![]() ,
,![]()
![]() ,
,![]()
![]() .
.![]()
width
of
the delta energy is over 100 MeV.)
Pion resonances of interest involve the 775 MeV rho ![]() )
)![]() )
)![]() )
)![]()
Older references like [36] picture the resonances
as correlated multi-pion states. However, quantum chromedynamics has
been associating actual particles with them. Take the rho, for
example. In [36] it is pictured as a two-pion
correlated state. (A true bound state of two 140 MeV pions should
have an energy less than 280 MeV, not 775 MeV.) However, quantum
chromedynamics identifies a rho as a single excited pion with a 775
MeV rest mass. It does decay almost instantly into two pions. The
omega, pictured as a three-pion correlated state, is according to
quantum chromedynamics a quantum superposition of half an up-antiup
and half a down-antidown quark pair, not unlike the neutral rho. It
usually decays into three pions. Quantum chromedynamics describes the
![]()
The rho and omega resonances appear to be important for the nucleon
repulsions at short range. And 3 and 4 pion exchanges have about the
same range as the ![]() .
.
One-meson exchanges are much easier to analyze than multi-meson ones. Therefore physicists may model the multi-pion processes as the exchange of one combined boson, rather than of multiple pions. That produces so-called “one-boson exchange potentials,” or “OBEP”s for short. They work surprisingly well.
The precise Yukawa potential that is produced depends on the spin and
parity of the exchanged boson, [36, pp. 176ff],
[[3]]. The pion has zero spin and negative parity. Such a
particle is often called “pseudoscalar.” Scalar means that its wave function at each
point is a just a number. However, normal numbers, like say a mass,
do not change sign if the directions of the axes are inverted. The
eta is a ![]()
However, the rho and omega are ![]()
Unfortunately, to describe the attractive forces in the intermediate
range, OBEP models need a roughly 600 MeV ![]()
scalar
boson. In fact, many OBEP models use both a 500 MeV and a 700 MeV
scalar boson.
The existence of such scalar resonances has never been accepted.
While an older reference like [36, pp. 172] may
point to a perceived very wide resonance at 700 MeV, how convincing
can a 700 MeV resonance with a width of at least 600 MeV be? This
lack of physical justification does detract from the OBEP potentials.
And of course, they are approximations in any case. There are important issues like multi-nucleon interactions and electromagnetic properties that probably only a comprehensive description of the actual exchange processes can correctly describe, [[3]]. Despite much work, nuclear potentials remain an active research area. One author already thinks in terms of millennia, [32].